数据信息包括数值型数据和非数值型数据两大类。其中数值型数据用于表示整数和实数之类数值型数据的信息，其表示方式涉及数的位权、基数、符号、小数点等问题；非数值型数据用于表示字符、声音、图形、图像、动画、影像之类的信息，其表示方式主要涉及代码的约定问题。根据计算机处理的不同要求，需要对数据采用不同的编码方式进行表示。

本章我们主要会讲述二进制数据表示中的原码、反码、补码、移码等数据编码方法和特点；定点数、浮点数、字符、汉字的二进制编码表示方法。

1. 数制转换

根据任何两个有理数相等，这两个有理数的整数部分和小数部分分别相等的原则，以按权展开多项式为基础，可以进行不同进制数之间的等值转换。

在不同进制数的转换时，应注意以下几个方面的问题：

1） 不同进制数的基数不同，所使用的数字的取值范围也不同

2） 将任意进制数转换为10进制数的方法是“按权相加”，即利用按权展开多项式将系数xi与位权值相乘后，将乘积逐项求和。

3） 将十进制数转换为任意进制数时，整数部分与小数部分需分别进行转换。整数部分的转换方法是“除基取余”，小数部分的转换方法是“乘基取整”。

• 利用除基取余法将十进制整数转换为R进制整数的规则：

(1) 把被转换的十进制整数除以基数R， 所得的余数即为R进制整数的最低位数字

(2) 将前次计算所得到的商再除以基数R，所得到的余数及为R进制整数的相应位数字

(3) 重复上面的步骤（2），直到商为0为止

• 利用乘基取整法将十进制小数转换为R进制小数的规则

(1) 把被转换的十进制小数乘以基数R，所得乘积的整数部分即为R进制小数的最高位数字

(2) 将前次计算所得到的乘积的小数部分再乘以基数R，所得新的乘积的整数部分即为R进制小数的相应位数字。

(3) 重复上面的步骤(2)，直到乘积的小数部分为0或求得所要求的位数为止

4） 因为2^3=8, 2^4=16, 所以二进制数与八进制数、十六进制数之间的转换可以利用它们之间的对应关系直接进行转换

• 将二进制数转换为八进制数的方法

(1) 将二进制的整数部分从最低有效位开始，每三位二进制数对应一位八进制数，不足三位高位补0

(2) 将二进制数的小数部分从最高有效位开始，每三位二进制数对应一位八进制数，不足三位，低位补0 

• 将二进制数转换为十六进制数的方法

(1) 将二进制的整数部分从最低有效位开始，每四位二进制数对应一位十六进制数，不足四位高位补0

(2) 将二进制数的小数部分从最高有效位开始，每四位二进制数对应一位十六进制数，不足四位，低位补0 

下面给出一个例子，将(116.8125)10转换为二进制数：

1） 首先利用除基取余法，进行整数部分的转换，得

                (116)10 = (1110100)2

2) 利用乘基取整法，进行小数部分的转换，得

                (0.8125)10 = (0.1101)2

因此，(116.8125)10 = (1110100.1101)2

2. 带符号数的表示

由于计算机只能直接识别和处理用0、1两种状态表示的二进制形式的数据，所以在计算机中无法按人们日常的书写习惯用正、负符号加绝对值来表示数值，而与数字一样，需要用二进制代码 0 和 1 来表示正、负号。这样，在计算机中表示带符号的数值数据时，数符和数据均采用0、1进行了代码化。这种采用二进制表示形式的连同数符一起代码化了的数据，在计算机中统称为机器数或机器码。而与机器数对应的用正、负符号加绝对值来表示的实际数值称为真值。

机器数可以分为无符号数和有符号数两种。无符号数是指计算机字长的所有二进制位均表示数值；而有符号数是指机器数分为符号和数值两部分，且均用二进制代码表示。

例如 设某机器的字长为8位，无符号整数在机器中的表示形式为：

带符号整数在机器中的表示形式为：

分别写出机器数10011001作为无符号整数和带符号整数对应的真值。

10011001 作为无符号整数时，对应的真值是(10011001)2 = (153)10

10011001 作为有符号整数时，其最高位的数码1代表符号"-"，所以与机器数10011001对应的真值是(-0011001)2 = (-25)10

综上所述，可得机器数的特点为：

1） 数的符号采用二进制代码化，0代表+, 1代表-。通常将符号的代码放在数据的最高位。

2） 小数点本身是隐含的，不占用存储空间

3） 每个机器数数据所占用的二进制位数受机器硬件规模的限制，与机器字长有关。超过机器字长的数值要舍去。

例如： 如果要将数 x=+0.101100111在字长为8位的机器中表示为一个单字长的数，则只能表示为01011001，最低位的两个1
无法在机器中表示。

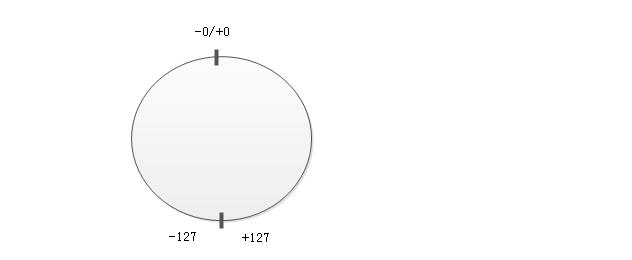
因为机器数的长度是由机器硬件规模规定的，所以机器数表示的数值是不连续的。例如8位二进制无符号数可以表示256个整数： 00000000 ~ 11111111可表示0~255； 8位二进制有符号数中： 00000000~01111111可表示0~127, 11111111~10000000可表示-127~0共256个数，其中00000000表示+0, 10000000表示-0。

3. 原码表示

原码表示是一种简单、直观的机器数表示方法，其表示形式与真值的形式最为接近。原码表示规定：机器数的最高位为符号位，0表示正数，1表示负数，数值部分在符号位后面，并以绝对值形式给出。

3.2 原码中0的表示

根据上式(2-2)和式(2-3)可知，在原码表示中，真值0有两种不同的表示形式，即+0和-0。

纯小数+0和-0的原码表示：

       [+0]原 = 0.00...00    [-0]原 = 1.00...00

纯正数+0和-0的原码表示：

       [+0]原 = 000...00     [-0]原 = 100...00

3.3 原码的左移和右移

3.4 原码的特点

（1） 原码表示直观、易懂，与真值的转换容易

（2） 原码表示中0有两种不同的表示形式，给使用带来了不便

通常0的原码用[+0]原表示，若在计算过程中出现了[-0]原，则需要硬件将[-0]原转换成[+0]原。

（3） 原码表示的加减运算复杂。

利用原码进行两数相加运算时，首先要判别两数符号，若同号则做加法，若异号则做减法。在利用原码进行两数相减运算时，不仅要判别两数符号，使得同号相减，异号相加；还要判别两数绝对值的大小，用绝对值大的数减去绝对值小的数，取绝对值大的数的符号为结果的符号。可见，原码表示不便于实现加减运算。

4. 补码表示

由于原码表示中0的表示形式不唯一，且原码加减运算不方便，造成实现原码加减运算的硬件比较复杂。为了简化运算，让符号位也作为数值的一部分参加运算，并使所有的加减运算均以加法运算来代替实现，人们提出了补码表示方法。

4.1 模的概念

补码表示的引入是基于模的概念。所谓“模”是指一个计数器的容量。比如钟表以12为一个计数循环，即可以看作以12为模。在进行钟表对时时，设当前钟表的时针停在9点钟的位置，要将时钟拨到4点钟，可以采用两种方法： 一种是反时针方向拨动指针，使指针后退5个小时，即9-5=4; 另一种是顺时针方向拨动指针，使时针前进7个小时，也能够使时针指向4。这是因为钟表的时间只有1、2、…、12这12个刻度，时针指向超过12时，将又指向1、2、…，相当于每超过12，就把12丢掉。由于 9 + 7 等于16，超过了12，因此把12减掉后得到4，即用 9 + 7也同样能够将钟表对准到4点钟。这样，对于采用12为模的钟表而言，9-5≡9+7(mod 12)，称为在模12的条件下，9-5等于9+7。这里，7称为-5对12的补数，即7=[-5]补 = 12+(-5)(mod 12)。如下图所示：

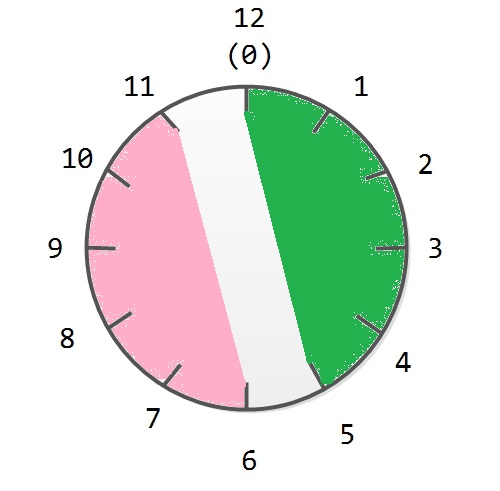
举个例子说明，对某一个确定的模而言，当需要减去一个数x时，可以加上对应的负数-x的补数[-x]补来代替。

4.2 补码的定义

在计算机中，由于硬件的运算部件与寄存器都有一定的字长限制，即计算机硬件能够一次处理的二进制数据的长度是有限的，因此计算机中的运算也是有模运算。例如一个位数为8的二进制计数器，计数范围为00000000~11111111，当计数满到11111111时，再加1，计数值将达到100000000，产生溢出，最高位的1被丢掉，使得计数器又从00000000开始计数。对于这个8位二进制计数器而言，产生溢出的量100000000就是计数器的模，相当于前述钟表列中的12。

4.3 补码的简便求法

给定一个二进制数x，如果需要求其补码，可以直接根据定义求得。但当x<0时，根据定义需要做减法运算，不太方便，因此可以采用以下简便方法：

1） 若 x>=0, 则[x]补 = x，并使符号位为0

2） 若 x<0， 则将x的各位取反，然后在最低位加 1，并使得符号位为 1，即得到[x]补

5. 反码表示

反码表示也是一种机器数，它实质上是一种特殊的补码，其特殊之处在于反码的模比补码的模小一个最低位上的1。

5.1 反码的定义

5.2 反码的特点

1) 在反码表示中，用符号位x0表示数值的正负，形式与源码表示相同，即0为正；1为负

2） 在反码表示中，数值0有两种表示方法：

6. 移码表示

从上面补码的几何性质中可以看到，如果将补码的符号部分与数值部分统一起来看成数值，则负数补码的值大于正数补码的值，这样在比较补码所对应的真值大小时，就不是很直观和方便，为此提出了移码表示。

6.1 移码的定义

6.2 移码的特点

7. 代码示例

如下代码程序(number_rep.c):

#include <stdio.h>
#include <stdlib.h>


int main(int argc, char *argv[])
{
    int a = 128;
    char b = (char)a;
    printf("b: %d\n", b);

    char c = -250;
    int d = (int)c;
    printf("d: %d\n", d);

    char e[17] = {0, 0, 0, 0, 0, 0, 0, 0, -520, 0, 0, 0, 0, 0, 0, 0, 0};
    int f = (int)e[8];
    unsigned char g = (unsigned char)e[8];
    printf("f: %d\n", f);
    printf("g: %d\n", g);

    unsigned char h = 520;
    int i = (int)g;
    char j = (char)g;
    printf("i: %d\n", i);
    printf("j: %d\n", j);


    return 0x0;
}

编译运行：

# gcc -g -o number_rep number_rep.c 
number_rep.c: 在函数‘main’中:
number_rep.c:11:14: 警告：隐式常量转换溢出 [-Woverflow]
     char c = -250;
              ^
number_rep.c:15:43: 警告：隐式常量转换溢出 [-Woverflow]
     char e[17] = {0, 0, 0, 0, 0, 0, 0, 0, -520, 0, 0, 0, 0, 0, 0, 0, 0};
                                           ^
number_rep.c:21:23: 警告：大整数隐式截断为无符号类型 [-Woverflow]
     unsigned char h = 520;
                       ^~~

#  ./number_rep 
b: -128
d: 6
f: -8
g: 248
i: 248
j: -8

gdb调试如下：

# gdb ./number_rep
GNU gdb (GDB) Red Hat Enterprise Linux 7.6.1-94.el7
Copyright (C) 2013 Free Software Foundation, Inc.
License GPLv3+: GNU GPL version 3 or later <http://gnu.org/licenses/gpl.html>
This is free software: you are free to change and redistribute it.
There is NO WARRANTY, to the extent permitted by law.  Type "show copying"
and "show warranty" for details.
This GDB was configured as "x86_64-redhat-linux-gnu".
For bug reporting instructions, please see:
<http://www.gnu.org/software/gdb/bugs/>...
Reading symbols from /data/home/lzy/just_for_test/number_rep...done.
(gdb) l 16
11          char c = -250;
12          int d = (int)c;
13          printf("d: %d\n", d);
14      
15          char e[17] = {0, 0, 0, 0, 0, 0, 0, 0, -520, 0, 0, 0, 0, 0, 0, 0, 0};
16          int f = (int)e[8];
17          unsigned char g = (unsigned char)e[8];
18          printf("f: %d\n", f);
19          printf("g: %d\n", g);
20      
(gdb) b number_rep.c:16
Breakpoint 1 at 0x40058e: file number_rep.c, line 16.
(gdb) r
Starting program: /data/home/lzy/just_for_test/./number_rep 
b: -128
d: 6

Breakpoint 1, main (argc=1, argv=0x7fffffffe048) at number_rep.c:16
16          int f = (int)e[8];
Missing separate debuginfos, use: debuginfo-install glibc-2.17-307.el7.1.x86_64
(gdb) p &e[0]
$1 = 0x7fffffffdf30 ""
(gdb) x/17xb 0x7fffffffdf30
0x7fffffffdf30: 0x00    0x00    0x00    0x00    0x00    0x00    0x00    0x00
0x7fffffffdf38: 0xf8    0x00    0x00    0x00    0x00    0x00    0x00    0x00
0x7fffffffdf40: 0x00
(gdb) 

源代码分析如下：

7.1 关于整形溢出

C语言的整形问题相信大家并不陌生了。对于整形溢出，分为无符号整形溢出和有符号整形溢出。

对于unsigned整形溢出，C语言的规范是有定义的————溢出后的数会以2^(8*sizeof(type))作模运算。也就是说，如果一个unsigned char溢出了，会把溢出的值与256求模。例如：

unsigned char x = 0xff;

print("%d\n", ++x);

上面的代码会输出: 0(因为0xff+1是256， 与2^8求模后就是0）。

对于signed整形的溢出，C的规范定义是”undefined behavior”。也就是说，编译器爱怎么实现就怎么实现。对于大多数编译器来说，算的啥就是啥。比如：

signed char x = 0x7f;

printf("%d\n", ++x);

上面的输出为：-128，因为0x7f+0x01得到的是0x80，也就是二进制的0b1000 0000，将该补码表示转换成真值即为-128。