数据结构之2-3树
2-3树是最简单的B-树(Balanced tree)结构,其每个非叶子节点都有2个或3个子女,而且所有叶子都在同一层上。虽然2-3树在实际应用中不多,但是理解2-3树对理解红黑树具有很大的帮助。
1. 定义
一棵2-3查找树或为一棵空树,或由以下节点组成:
-
2-节点: 含有一个键(及其对应的值)和两条链接, 左链接指向的
2-3树中的键都小于该节点,右链接指向的2-3树中的键都大于该节点; -
3-节点: 含有两个键(及其对应的值)和三条链接, 左链接指向的
2-3树中的键都小于该节点, 中链接指向的2-3树中的键都位于该节点的两个键之间,右链接指向的2-3树中的键都大于该节点;
和以前一样,我们将指向一棵空树的链接称为空链接。2-3查找树如下图所示:
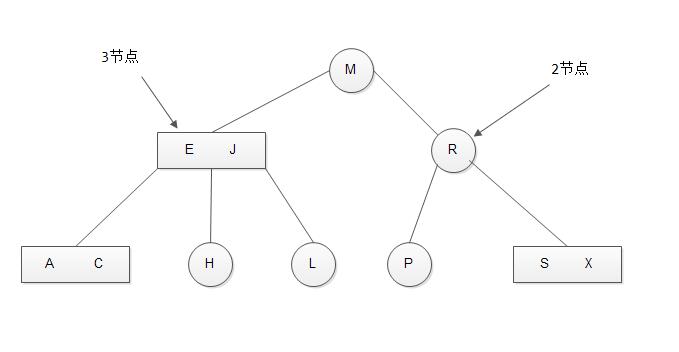
一棵完美平衡的2-3查找树所有空链接到根节点的的距离都相同。下面讲述一下2-3查找树的基本操作:
-
查找节点
-
插入节点
-
变换
-
生长
-
构造2-3树
-
删除节点
2. 查找节点
要判断一个键是否存在树中,先将它和根节点中的键比较, 如果它和其中任意一个相等,查找命中; 否则就根据比较的结果找到指向相应区间的链接,并在其指向的子树中递归地继续查找, 如果找到了空链接上,则查找未命中。
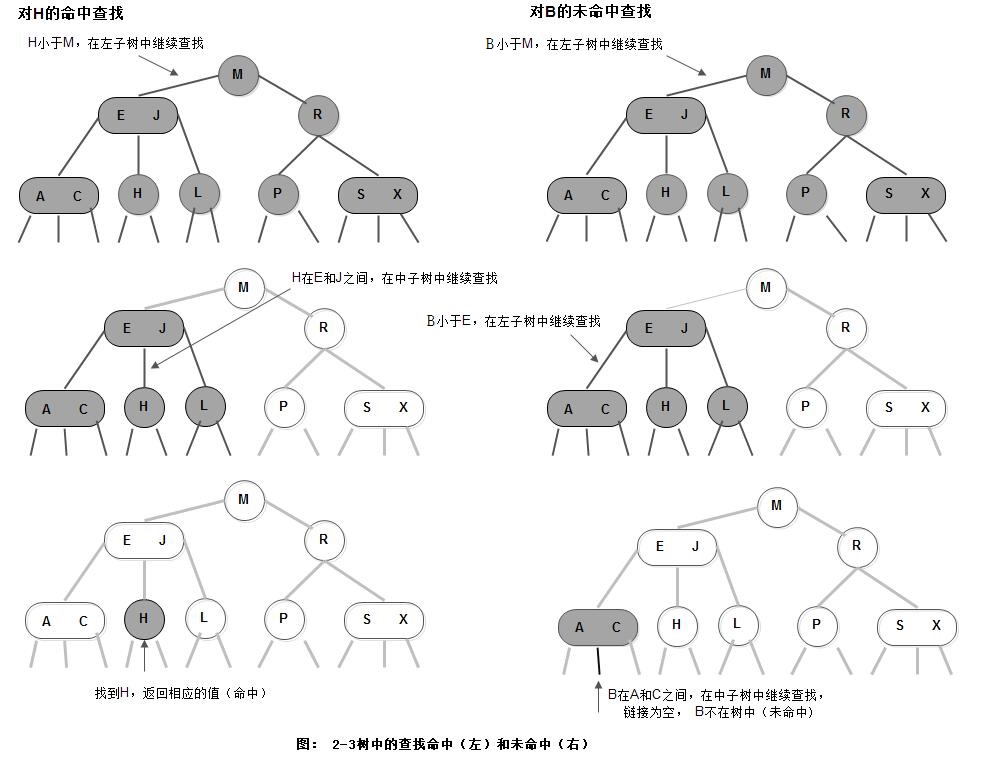
3. 插入节点
要在2-3树中插入一个新节点,我们可以和二叉查找树一样对2-3树进行一次未命中查找,然后把新节点挂在树的底部。但这样的话无法保证2-3树的完美平衡性。我们使用2-3树的主要原因在于它能够在插入之后继续保持平衡。下面我们根据未命中查找结束时的节点类型,分多种不同情况说明:
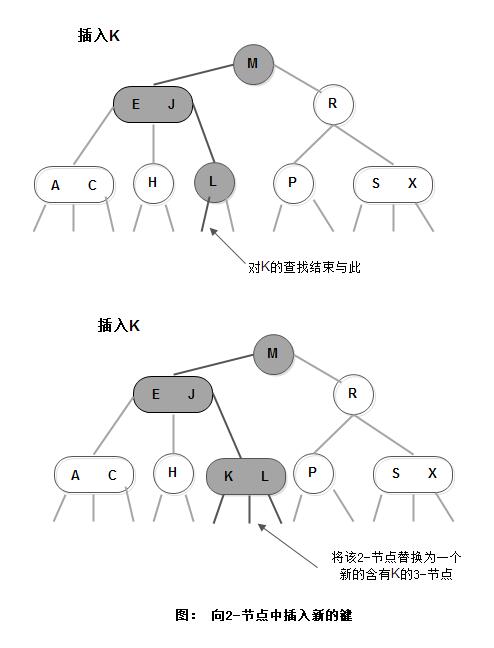
1) 向2-节点中插入新键
当未命中查找结束于一个2-节点时,直接将2-节点替换为一个3-节点,并将要插入的键保存其中:
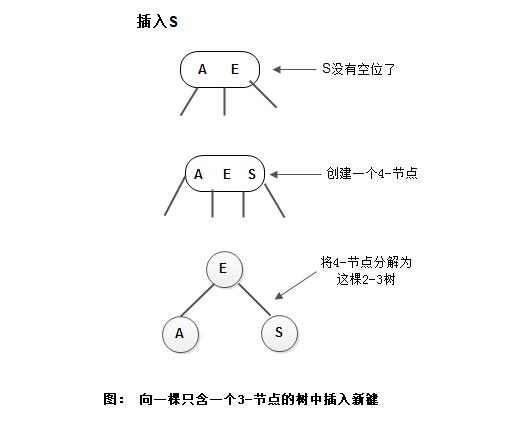
2) 向一棵只含3-节点的树中插入新键
先临时将新键存入唯一的3-节点中,使其成为一个4-节点,再将它转化为一棵由3个2-节点组成的2-3树,分解后树高会增加1:
3) 向一个双亲节点为2-节点的3-节点中插入新键
先构造一个临时的4-节点并将其分解,分解时将中键移动到双亲节点中(中键移动后,其双亲节点的中的位置由键的大小确定):
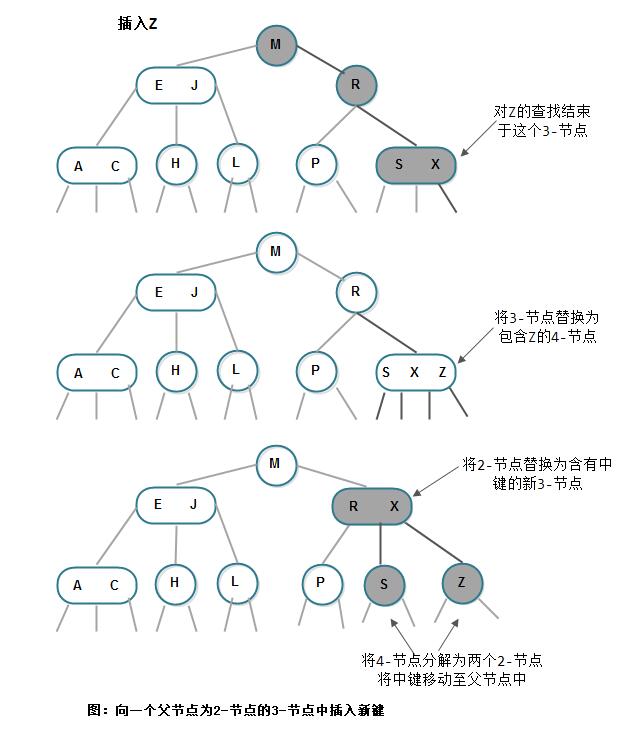
4) 向一个双亲节点为3-节点的3-节点插入新键
一直向上分解构造的临时4-节点,并将中键移动到更高层双亲节点,直到遇到一个2-节点并将其替换为一个不需要继续分解的3-节点,或者是到达树根(3-节点)
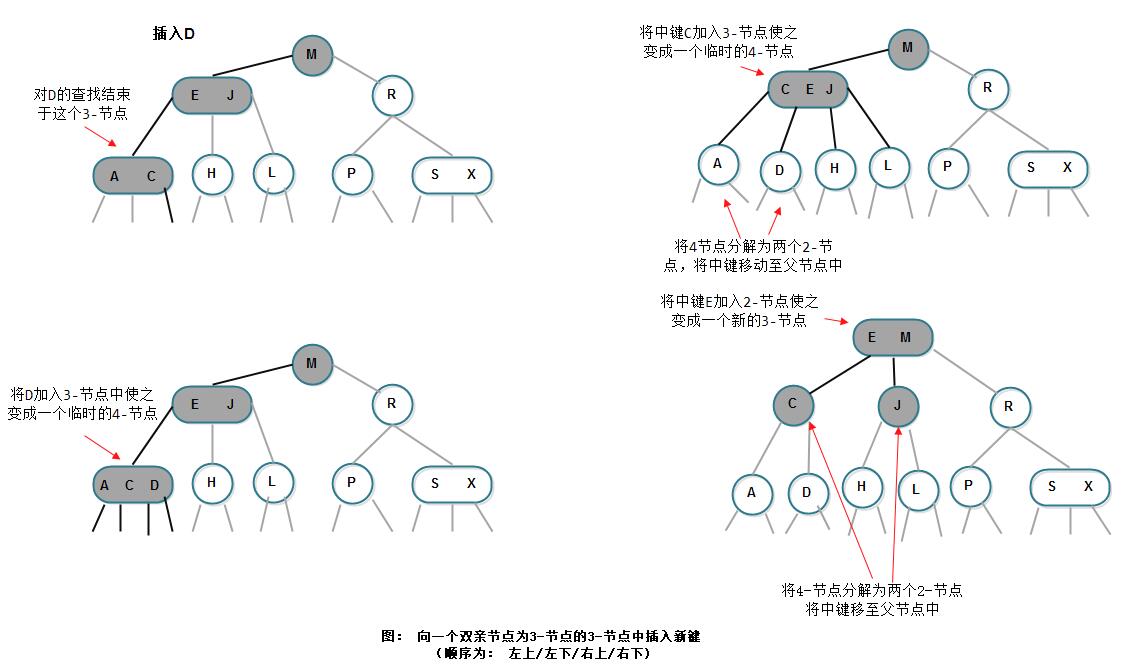
5) 分解根节点
如果从插入节点到根节点的路径上全是3-节点,根将最终被替换为一个临时的4-节点,将临时的4-节点分解为三个2-节点,分解后树高会增加1:
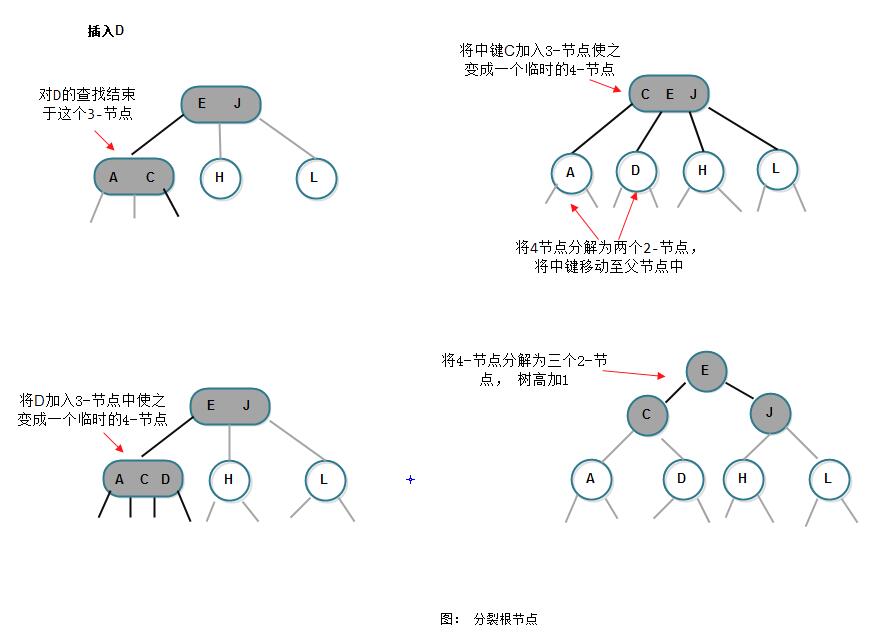
我们对上面的5中插入情况进行总结:
先找插入节点, 若节点有空(即2-节点),则直接插入。如果节点没空(3-节点),则插入使其临时容纳这个元素,然后分裂此节点,把中间元素
移动到其父节点中, 对父节点亦如此处理。(中键一直往上移,直到找到空位,在此过程中没有找到空位就先搞一个临时的,再分裂)
2-3树插入算法的根本在于这些变换都是局部的: 除了相关的节点和链接之外不必修改或者检查树的其他部分。每次变换中,变换的链接数量不会
超过一个很小的常数。所有局部变换都不会影响整棵树的有序性和平衡性。4. 变换
1) 局部变换
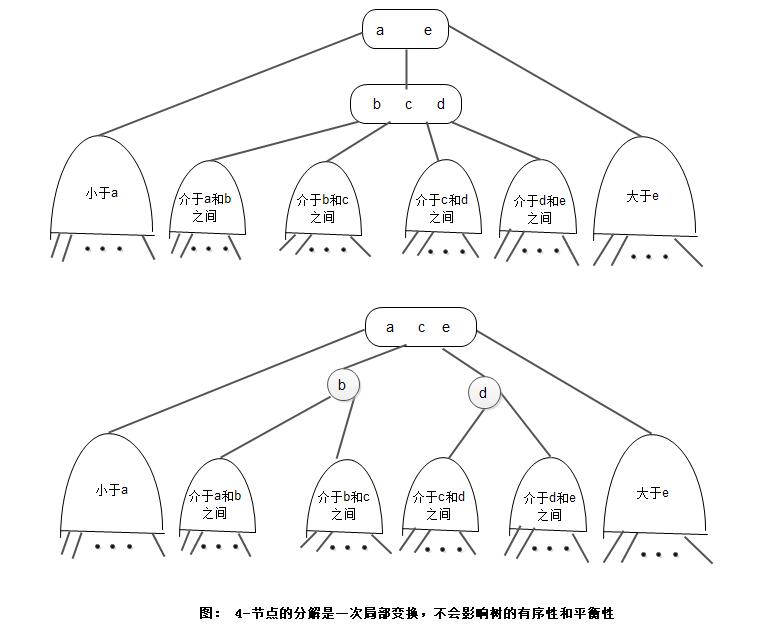
这里我们将对一个4-节点的分解叫做变换,对一个4-节点的变换方式可能有6种:
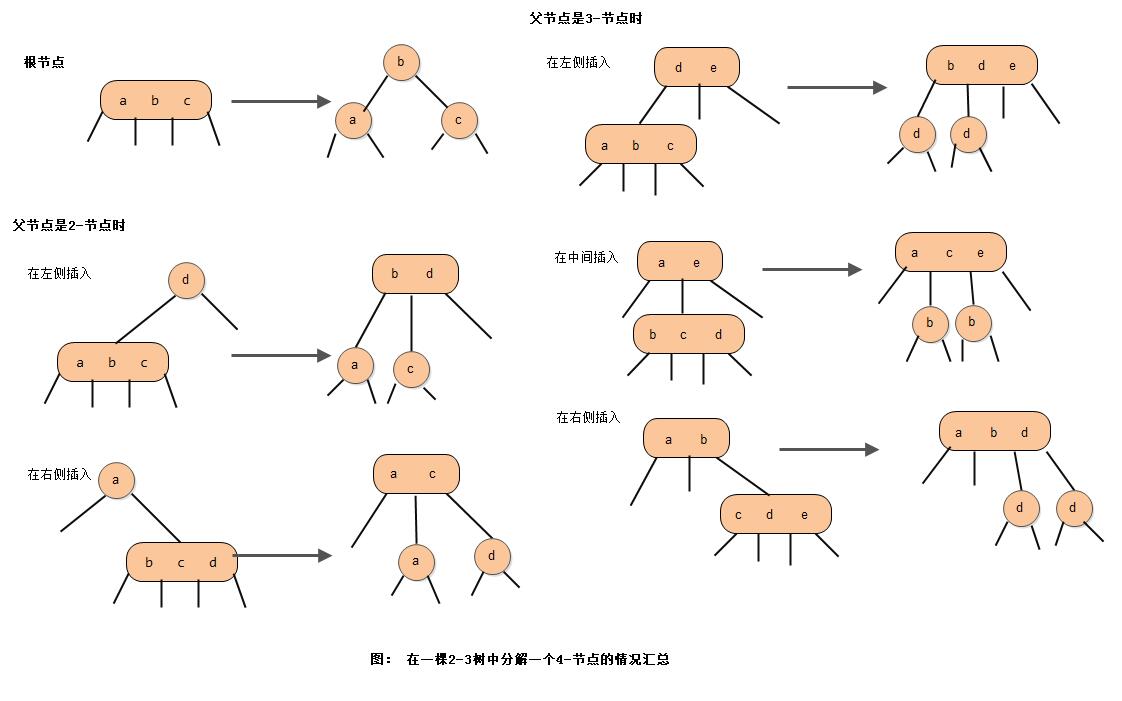
2) 全局性质
变换不会影响树的全局有序性和平衡性,任意空链接到根节点的路径长度依旧是相等的:
5. 生长
和标准二叉查找树由上向下生长不同,2-3树的生长是由下向上的。
6. 删除
首先我们找到要删除的关键字(假设是K)所在的节点。如果这个节点不是叶节点,就要找到中序排列时 K 后面的关键字所在的节点,这个节点一定是叶节点。然后交换这两个关键字,那么所删除的关键字最终还是在一个叶节点中。这里叶节点可以分成两种情况:
1. 叶节点是 3-节点 2. 叶节点是 2-节点
6.1 删除 3-节点类型的叶节点
此种情况非常简单,只需要将该3-节点变成2-节点即可,删除并不会影响树高。
6.2 删除 2-节点 类型的叶节点
首先这里又可以分为两种大的情况:
1. 该叶节点的父节点是 3-节点 2. 该叶节点的父节点是 2-节点
下面我们针对这两种情况再细分讲解:
(1) 叶节点的父节点是 3-节点
情形1: 删除节点是左孩子,中间孩子是2-节点
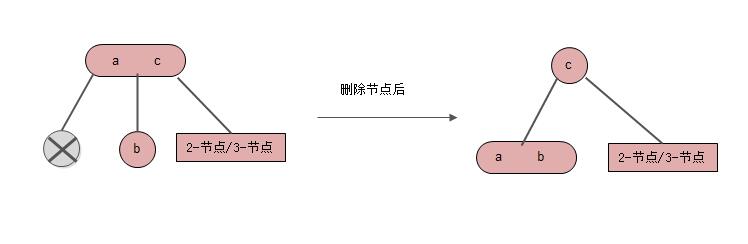
如上图,以关键字a、b构造一个3-节点,并将其作为c的左孩子
情形2: 删除节点是左孩子,中间孩子是3-节点
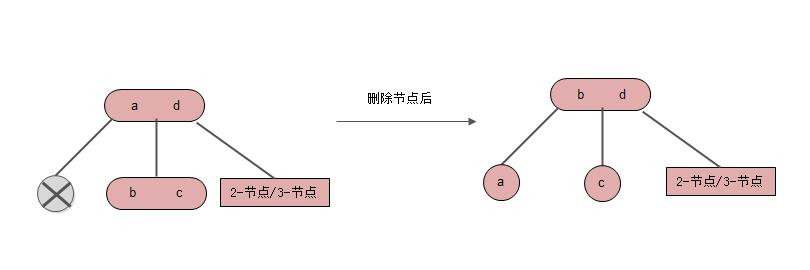
情形3: 删除节点是中间节点, 右节点是2-节点

情形4: 删除节点是中间节点, 右节点是3-节点
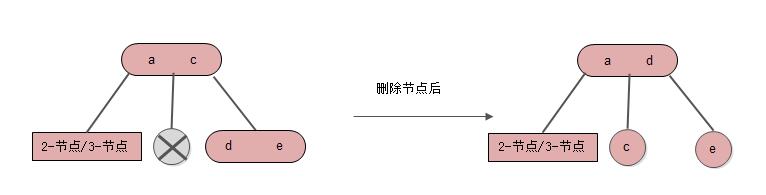
情形5: 删除节点是右节点, 中间节点是2-节点
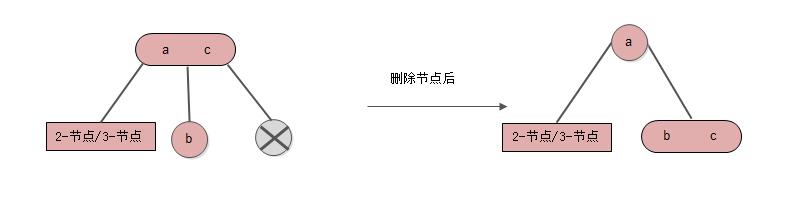
情形6: 删除节点是右节点, 中间节点是3-节点
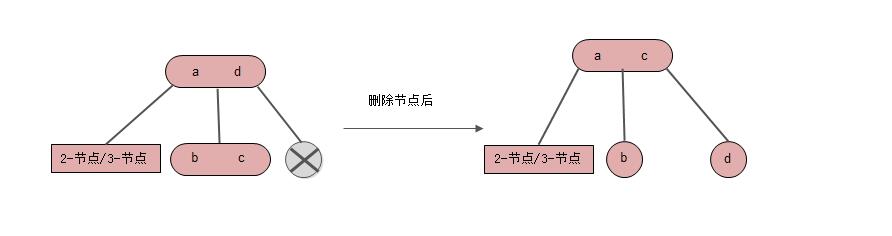
(2) 叶节点的父节点是 2-节点
情形1: 删除节点是左节点,右节点是2-节点
首先将其兄弟节点与父节点合并,形成一个3-节点(假设为P), 此时P到根节点的高度等于 树高 减1。 将P节点作为当前节点,设置当前树高度为h = -1, 执行如下步骤:
a) 如果当前节点并没有兄弟节点, 则说明已经到了根节点, 退出
b) 如果当前节点兄弟节点不是2-节点,则父节点中的key下移到该节点,兄弟节点中的一个key上移。接着分解该兄弟节点, 此时树高增加1,
即h = h+1。 如果h值为0,说明整颗树已经达到平衡, 退出; 否则, 将当前节点设置为该兄弟节点(这里指兄弟节点key上移后的节
点), 继续执行a) b) c) d)步骤;
c) 如果兄弟节点是2-节点,父节点为3-节点,将父节点中的key与兄弟节点合并,再将“当前节点”作为该合并后节点的一棵子树, 此时树高增加1,
即h = h+1。 如果h值为0, 说明整颗树已经达到平衡, 退出; 否则, 将当前节点设置为该合并后的兄弟节点, 继续执行a) b) c) d)步骤;
d) 如果兄弟节点是2-节点, 父节点是2-节点, 则将父节点的key与兄弟节点中的key合并,形成一个3-节点, 将当前节点作为该合并节点
的一棵子树 , 此时树高减1, 即h = h -1。将当前节点设置为该合并节点,接着继续执行a) b) c) d)步骤
注: 上面的h可以理解为P所指向的树的高度相对于整个树的高度之差。另上面关于高度h的变化有些地方可能表述不准确
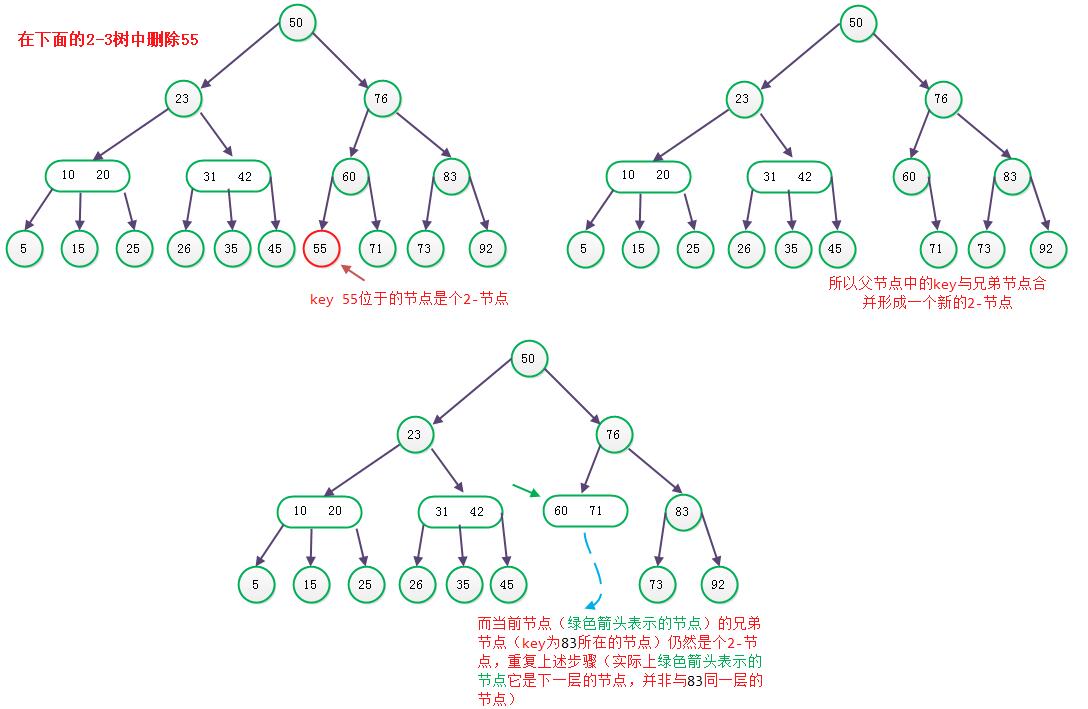
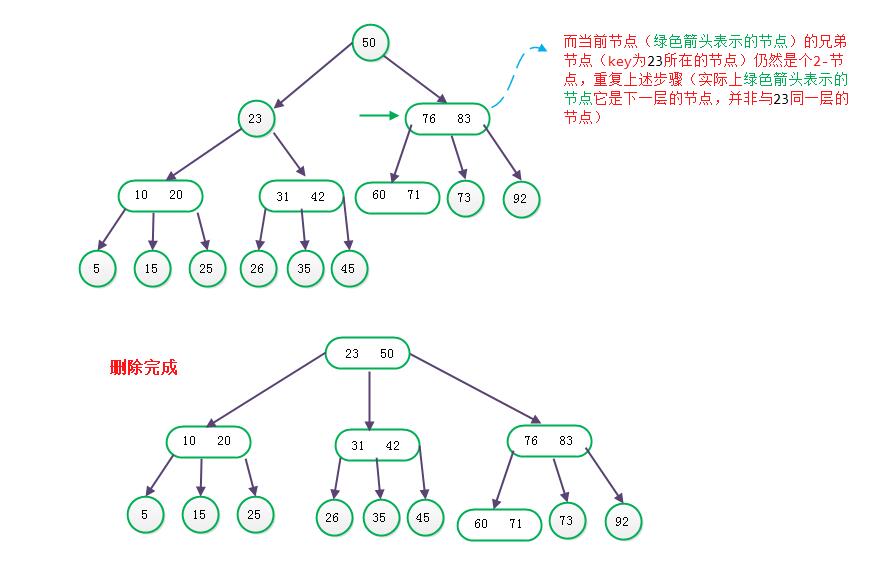
情形2: 删除节点是左节点,右节点是3-节点
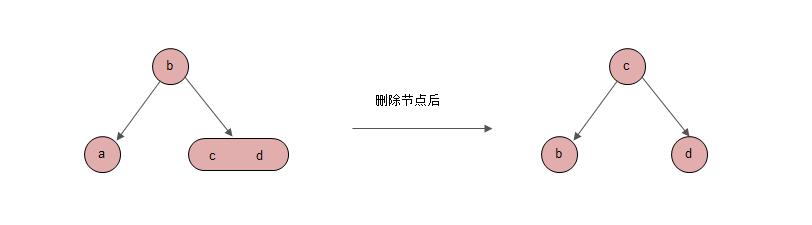
情形3: 删除节点是右节点,左节点是2-节点
(此种情况与上面 情形1类似,这里不再赘述)
情形4: 删除节点是右节点,左节点是3-节点
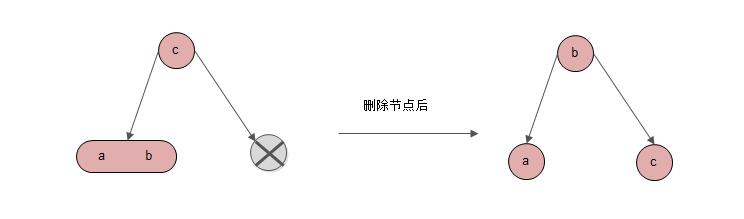
6.3 删除总结
上面我们细分成了多种不同的子情况,其实对于有些情形我们可以一并处理。下面做一个总结:
(1) 如果2-3树中不存在当前需要删除的key,则删除失败
(2) 如果当前需要删除的key不位于叶子节点上,则找到该节点的直接后继(中序遍历)节点,该节点一定是叶子节点。然后将这两个节点的key进行交换, 转换成步骤(3)
(3) 如果当前要删除的key位于叶子节点上:
(3.1) 如果该节点不是2-节点,删除key, 结束
(3.2) 如果该节点是2-节点, 删除该节点(当前节点):
(3.2.1) 如果兄弟节点不是2-节点,则将父节点中的key下移到“该节点”(这里指当前节点),兄弟节点中的一个key上移
(3.2.2) 如果兄弟节点是2-节点,父节点是3-节点,将父节点中的key下移与兄弟节点合并
(3.2.3) 如果兄弟节点是2-节点,父节点也是一个2-节点,父节点中的key与兄弟节点中的key合并,形成一个3-节点,把此节点
看成当前节点(此节点实际上是下一层的节点),重复3.2.1到3.2.3
注: 如果是在2-节点(叶子节点)中进行删除,每次删除会减少一个分支,如果删除操作导致根节点参与合并,则2-3树会降低一层。
7. 示例代码参考
struct node23{
void *value;
struct node23 *parent;
struct node23 *left;
struct node23 *right;
void *extra;
struct node23 *middle;
};
typedef struct node23 * root;
void insert(root *r, struct node23 *node, void *value){
struct node23 *p = node;
struct tempnode{
int type; //2--二节点 3--三节点 4--四节点 其他--非法
void *value[3];
struct tempnode *children[4];
struct node23 *origin;
};
struct tempnode t = {
2,
{value, NULL, NULL},
{NULL, NULL, NULL, NULL},
NULL,
};
//将p与t节点进行合并
while(p){
if (!p->extra){
if (t.type == 2){
}else if(t.type == 4){
}else{
return ERROR;
}
return SUCCESS;
}else{
parent = p->parent;
if (t.origin == NULL){
}else if(p->left == origin){
}else if(p->right == origin){
}else{
}
p = parent;
}
}
newnode = (struct node23 *)malloc(sizeof(struct node23));
newnode->value = t.value[2];
newnode->left = t.children[2];
newnode->right = t.children[3];
newnode->extra = NULL;
newnode->middle = NULL;
origin->value = t.value[0];
origin->left = t.children[0];
origin->right = t.children[1];
origin->extra = NULL;
origin->middle = NULL;
rnode = (struct node23 *)malloc(sizeof(struct node23));
rnode->value = t.value[1];
rnode->left = origin;
rnode->right = newnode;
rnode->extra = NULL;
rnode->middle = NULL;
rnode->parent = NULL;
newnode->parent = origin->parent = rnode;
*r = rnode;
return SUCCESS;
}
void tranverse_inorder(root r)
{
if(r){
tranverse_inorder(r->left);
tranverse_print(r->value);
if(r->extra){
tranverse_inorder(r->middle);
tranverse_printf(r->extra);
}
tranverse_inorder(r->right);
}
}上述插入过程,其实可以看成是如下图所示的一个临时节点合并到父节点的过程。
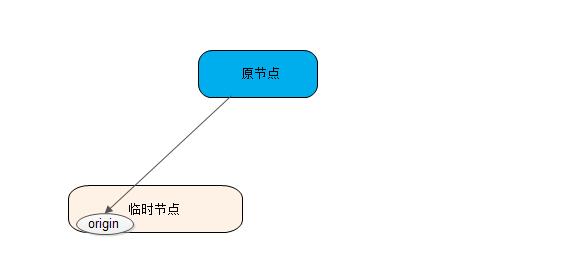
8. 数据结构定义
此外,我们也可以按照如下方式来定义数据结构:
struct TTNode;
struct TwoNode{
int key;
struct TTNode *left;
struct TTNode *right;
struct TTNode *parent;
};
struct ThreeNode{
int lkey;
int rkey;
struct TTNode *left;
struct TTNode *middle;
struct TTNode *right;
struct TTNode *parent;
};
typedef enum{TWO_NODE, THREE_NODE}NodeType;
struct TTNode{
NodeType type;
union{
TwoNode twNode;
ThreeNode thNode;
};
};
[参看]:

