深入理解二叉搜索树（BST）

本文主要讲述一下二叉搜索树相关原理及操作。

1. 二叉搜索树

二叉查找树（Binary Search Tree），又称为二叉搜索树或二叉排序树。它或者是一棵空树，或者是具有下列性质的二叉树: 若它的左子树不空，则左子树上所有节点的值均小于它根节点的值；若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；它的左、右子树也分别为二叉排序树。

2. 节点查找

在二叉搜索树b中查找x的过程如下：

若b是空树，则搜索失败，否则：

若x等于b的根节点的数据域之值，则查找成功；否则：
若x小于b的根节点的数据域之值， 则搜索左子树； 否则：
搜索右子树

ds-bst-search

下面给出BST查找的递归算法与非递归算法：

1）递归算法

struct BSTNode *search(BSTNode *root, int key)
{
    if(!root || root->key == key)
		return root;
    else if(key < root->key)
        return search(root->left, key);
    else
        return search(root->right, key);
}

2) 非递归算法

struct BSTNode *search(BSTNode *root, int key)
{
	BSTNode *p = root;
	while(p)
	{
		if(p->key == key)
			return p;
		else if(p->key > key)
			p = p->left;
		else
			p = p->right;
	}

	return p;
}

3. 前驱与后继

对于给定的一棵二叉搜索树，如果所有节点的key均不相同，那么节点x的前驱是指小于x.key的最大关键字节点；而一个节点x的后继是指大于x.key的最小关键字节点。

1） x节点后继

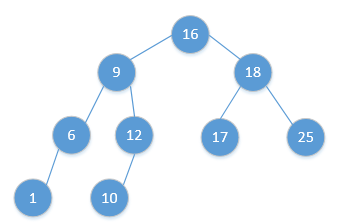
现在我们考虑如何求解一个节点x的后继。对于节点x，如果其右子树不为空，那么x的后继一定是其右子树的最左边的节点。而如果x的右子树为空，并且有一个后继，那么其后继必然是x的最底层的祖先，并且后继的左孩子也是x的一个祖先，因此为了找到这样的后继节点，只需要从x开始沿着树向上移动，直到遇到一个节点，这个节点是其双亲的左孩子。（例如：上图中节点12的后继节点是16）

下面给出求后继节点的伪代码：

struct BSTNode *successor(BSTNode *x)
{
	if(x->right)
	{
		x = x->right;
		while(x->left)  x=x->left;
		return x;
	}

	parent = x->parent;
	while(parent && parent->right == x)
	{
		x=parent;
		parent = parent->parent;
	}

	return parent;
}

2) x节点的前驱

下面我们考虑如何求解一个节点x的前驱。对于节点x，如果其左子树不为空，那么x的前驱一定是其左孩子。而如果x的左子树为空，并且有一个前驱，那么其前驱必然是x的最底层的祖先，并且前驱的右孩子也是x的祖先，因此为了知道这样的前驱节点，只需要从x沿着树向上移动，直到遇到一个节点，这个节点是其双亲的右孩子。（例如：上图中的节点10的前驱节点是9）

下面给出求前驱节点的伪代码：

struct BSTNode *predecessor(BSTNode *x)
{
	if(x->left)
		return x->left;
	
	parent = x->parent;
	while(parent && parent->left == x)
	{
		x = parent;
		parent = parent->parent;
	}

	return parent;
}

4. BST节点插入

BST节点的插入非常简单，很类似于二叉搜索树的查找过程。当需要插入一个新节点时，从根节点开始，迭代或递归向下移动，直到遇到一个空指针。需要插入的值即被存储在该节点位置。下面给出迭代版插入的伪代码：

struct BSTNode *insert(BSTNode **root, struct BSTNode *node)
{
   BSTNode *p = *root;
   BSTNode *q = NULL;

   node->left = node->right = NULL;

   while(p)
   {
       if(p->key == node->key)
          return p;
       else if(p->key > node->key)
       {
          q = p;
          p = p->left;
       }
       else{
           q = p;
           p = p->right;
       }
   }

   if(!q)
   {
      *root = node;
   }
   else{
      if(q->key > node->key)
        q->left = node;
      else
        q->right = node;
   }

   return node;
}

下图给出插入节点17的示意图：

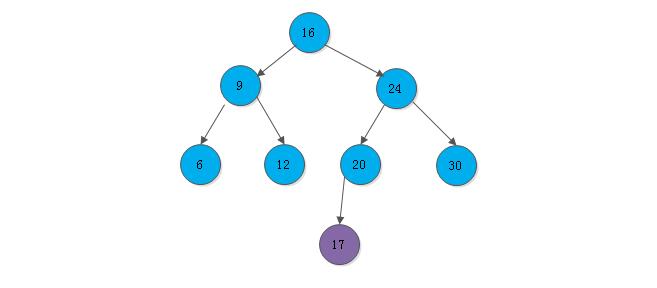
ds-bst-insert

同其他搜索树类似，二叉搜索树（BST）的插入操作的时间复杂度为O(h).

5. BST节点删除

二叉搜索树的节点的删除比插入较为复杂，总体来说，节点的删除可归结为三种情况：

如果节点z没有孩子节点，那么只需要简单的将其删除即可，并修改父节点，用NULL来替换z；
如果节点z只有一个孩子，那么将孩子节点提升到z的位置，并修改z的父节点，用z的孩子替换z；
如果节点z有两个孩子，那么查找z的后继y，此外后继一定在z的右子树中，然后让y替换z

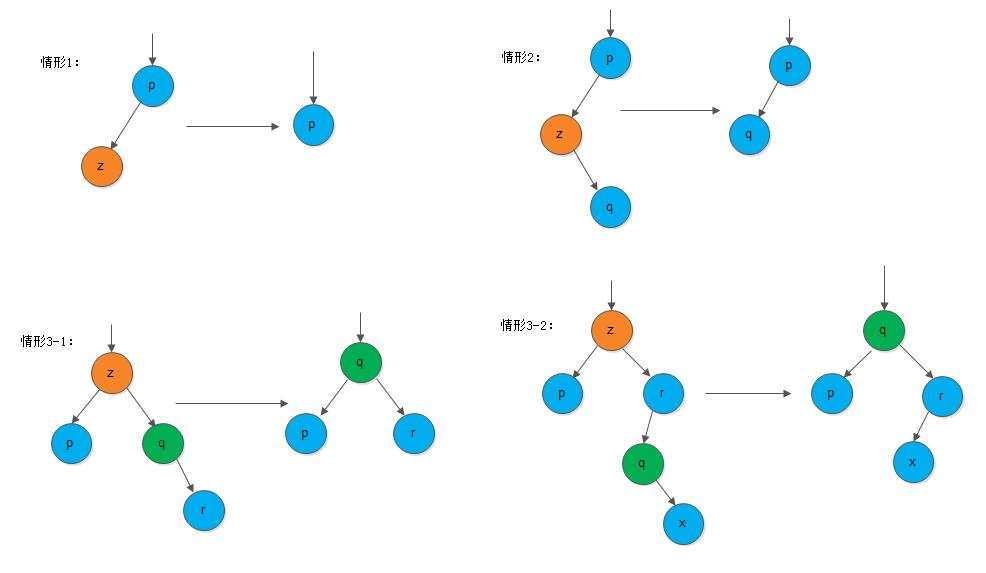
这三种情况中，前两种较为简单，3相对棘手，我们通过示意图描述这几种情况：

ds-bst-delete 从上图我们可以看到，针对情形3，又可以分出两种子情形：

(1) z的后继q位于右子树中，但没有左孩子

(2) z的后继q位于右子树中，但是并不是z的右孩子, 此时要用q的右孩子替换z

下面给出相应删除的伪代码：

int delete(struct BSTNode **root, int key)
{
      int i;
      struct BSTNode *p = *root;
      
      while(p)
      {
         if(p->key == key)
             break;
         else if(p->key < key)
             p = p->right;
          else
             p = p->left;
      }
      if(!p)
          return -1;

      i = (p->left==NULL?0:1) + (p->right==NULL?0:1);
      if(i == 0)
      {
          parent = p->parent;
          if(parent)
          {
              if(parent->left == p)
                   parent->left = NULL;
              else
                   parent->right = NULL;			  
          }		    
          else{
               *root = NULL;
          }
          free(p);
      }
      else if(i == 1)
      {
           parent  = p->parent;
           child = p->left ? p->left : p->right;
           if(parent)
           {
               if(parent->left == p)
                   parent->left = child;
               else
                   parent->right = child;

               child->parent =parent;
           }
           else{
                *root = child;
                child->parent = NULL;
           }
           free(p);
      }
     else{
          q = p->right;
          while(q->left) q=q->left;
          
          r = q->parent;
          child = q->right;
          parent = p->parent;
          left = p->left;

          if(r == p)
          {
               q->left = left;
               left->parent = q;
               if(parent)
               {
                   if(parent->left == p)
                      parent->left = q;
                   else
                      parent->right = q;

                   q->parent = parent;
               }
               else{
                   *root = q;
               }
             
          }
          else{
              q->left = left;
              left->parent = q;
              q->right = p->right;
              p->right->parent = q;
              r->left = child;
              child->parent = r;
              if(parent)
              {
                   if(parent->left == p)
                      parent->left = q;
                   else
                      parent->right = q;

                   q->parent = parent;
              }
              else{
                   *root = q;
              }
          }

          free(p);
     }
}

6. 二叉树的遍历

最后，我们考虑二叉搜索树的遍历。二叉搜索树的性质允许通过简单递归算法来输出树中所有的关键字，有三种方式：先序遍历、中序遍历、后序遍历。下面我们给出递归算法的实现伪代码：

先序遍历

void preorder_tranverse(struct BSTNode *root)
{
     if(!root)
         return;
     
      print_node(root);
      preorder_tranverse(root->left);
      preorder_tranverse(root->right);
}

中序遍历

void inorder_tranverse(struct BSTNode *root)
{
     if(!root)
         return;
     inorder_tranverse(root->left);
     print_node(root);
     inorder_tranverse(root->right);
}

后序遍历

void postorder_tranverse(struct BSTNode *root)
{
    if(!root)
       return;

    postorder_tranverse(root->left);
    postorder_tranverse(root->right);
    print_node(root);
}

6.1 二叉树的非递归遍历

仿照递归算法执行过程中递归工作栈的状态变化状况，可直接写出相应的非递归算法。例如，从中序遍历递归算法执行过程中递归工作栈的状态可见：（1）工作记录中包含两项，其一是递归调用的语句编号，其二是指向根节点的指针，则当栈顶记录中的指针非空时，应遍历左子树，即指向左子树根的指针进栈；（2）若栈顶记录中的指针值为空，则应退至上一层，若是从左子树返回，则应访问当前层即栈顶记录中指针所指的根节点；（3）若是从右子树返回，则表明当前层的遍历结束，应继续退栈。从另一个角度看，这意味着遍历右子树时，不再需要保存当前层的根指针，可直接修改栈顶记录中的指针即可。由此可得两个中序遍历二叉树的非递归算法如算法6.2和算法6.3所示，供读者分析比较，以加深理解。

算法6.2:

void inorder_tranverse(struct BSTNode *root)
{
	//采用二叉链表存储结构，中序遍历二叉树root
	InitStack(S);
	Push(S, root);
	
	while(!StackEmpty(S))
	{
		//向左走到尽头
		while(GetTop(S, p) && p) Push(S, p->left);

		//空指针退栈
		Pop(S, p);
		
		//访问节点，向右一步
		if(!StackEmpty(S))
		{
			Pop(S,p);
			print_node(p);
			Push(S,p->right);
		}
		
	}
}

算法6.3

void inorder_tranverse(struct BSTNode *root)
{
	InitStack(S);
	p = root;
	
	while(p || !StackEmpty(S))
	{
		if(p){
			//根指针进栈，遍历左子树
			
			Push(S, p);
			p = p->left;
		}else{
			//根指针退栈，访问根节点，遍历右子树
			
			Pop(S,p);
			print_node(p);
			p = p->rchild;
		}
	}
}

1) 前序遍历非递归算法

如下是先序遍历的非递归算法实现：

void preorder_tranverse(struct BSTNode *root){
	Stack S;
	struct BSTNode *p = root;
	
	InitStack(s);
	Push(S, p);
	
	while(!StackEmpty(S)){
		Pop(S, p);
		
		if(p){
			print_node(p);
			Push(p->right);
			Push(p->left);
		}
	}
	
}

2) 后序遍历非递归算法

下面我们再给出后序遍历的非递归算法的实现参考：

void postorder_tranverse(struct BSTNode *root)
{
	Stack S;
	struct BSTNode *p, *q, *pRight;
	
	InitStack(S);
	p = root;
	
	while(p || !StackEmpty(S))
	{
		if(p){
			Push(S, p);
			p = p->left;
		}else{
			GetTop(S, p);
			if(p->right){
				p = p->right;
			}else{
				Pop(S, p);
				print_node(p);
				
				pRight =NULL;
				while(!StackEmpty())
				{
					GetTop(S, q);
					
					if(q->right == p){
						Pop(S, q);
						print_node(q);
						p = q;
					}else{
						pRight = q->right;
						break;
					}
				
				}
			}
		
			p = pRight;
		
		}
	
	}

}

后序遍历算法实现2：

void postorder_tranverse(struct BSNode *root)
{
    Stack s;
    struct BSNode *tp, *q;
    int traceback = 0;

    InitStack(&s);
    push(s, root);

    while(!StackEmpty(s)){

        GetTop(s, &tp);
        if(tp){
            if(traceback == 0){
                push(tp->right);
                push(tp->left);
            }else{
                pop(s, &tp);
                print_node(tp);

                GetTop(s, q);
                if(q){
                    if (q->left == tp && q->right == tp){
                        //
                    }else{
                        traceback = 0;
                    }
                }
            }
        }else{
            pop(s, &tp);
            traceback = 1;
        }
    }
}

[参看]:

深入理解二叉搜索树（BST）

Ivanzz

发上等愿，结中等缘，享下等福；择高处立，寻平处住，向宽处行