B-树详解

本文详细介绍一下B树的实现。

1. B-树

B-tree树即B树, 这里B即Balanced的意思。因为B树的原英文名称为B-tree,而国内很多人喜欢把B-tree翻译为B-树, 其实这是个非常不好的直译，很容易让人产生误解。如人们可能会以为B-树是一种树，而B树又是另外一种树。事实上，B-tree就是指的B树，特此说明。

1.1 B-树的定义

B-树是一种平衡的多路查找树，它在文件系统中很有用。我们在这里先介绍一下这种树结构。

一颗m阶的B-树, 或为空树，或为满足下列特性的m叉树:

树中每个节点至多有m颗子树；
若根节点不是叶子节点，则至少有两颗子树
除根以外的所有非终端节点至少有⌈m/2⌉棵子树
所有的非终端节点中包含下列信息数据

     (n, A0, K1, A1, K2, A2, ... , Kn, An)

其中： Ki(i=1, ... ,n)为关键字，且Ki<Ki+1(i=1, ... ,n-1); Ai(i=0, ... ,n)为指向子树根节点的指针，且Ai-1所指子树中所有节点的关键字均小于Ki(i=1, ... ,n)，An所指子树中所有关键字均大于Kn，n(⌈m/2⌉-1 <= n<= m-1)为关键字的个数（n+1为子树个数)

所有的叶子节点都出现在同一层次上，并且不带信息（可以看作是外部节点或查找失败的节点，实际上这些节点不存在，指向节点的指针为空）

下图所示为一颗4阶的B-树, 其深度为4(F为叶子节点）:

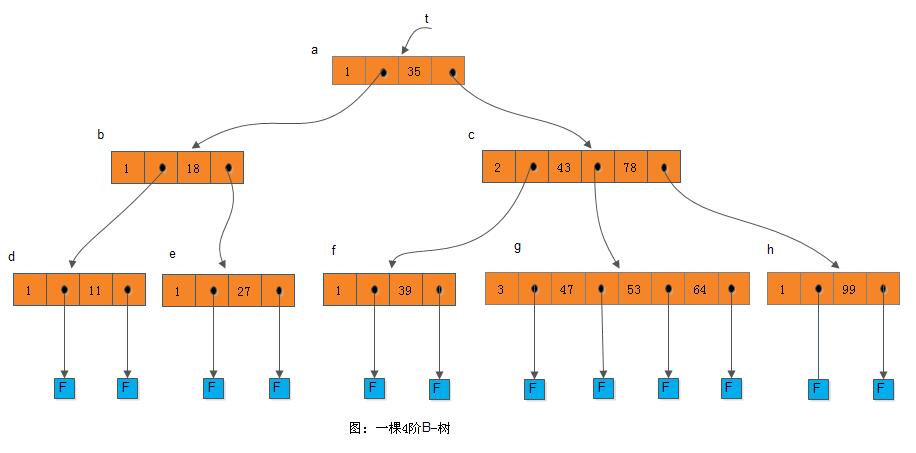
ds-btree

1.2 B-树的特性

由B-树的定义可以知道，其具有如下特性：

关键字集合分布在整棵树中；
任何一个关键字出现且只出现在一个节点中
搜索有可能在非叶子节点结束
其搜索性能等价于在关键字全集内做一次二分查找
自动层次控制：由于限制了除根节点以外的非叶子节点，至少含有⌈m/2⌉个儿子，确保了节点的至少利用率

2. B-树的查找

由B-树的定义可知，在B-树上进行查找的过程和二叉排序树的查找类似。例如，在上图所示的B树中查找关键字47的过程如下：首先从根开始，根据根节点指针t找到*a节点，因*a节点中只有一个关键字，且给定值47大于关键字35, 则若存在必在指针A1所指的子树内；顺指针找到*c节点，该节点有两个关键字(43和78)，而43<47<78,则若存在必在指针A1所指的子树中。同样顺指针找到*g节点，在该节点中顺序查找到关键字47, 由此查找成功。查找不成功的过程也类似，例如在同一棵树中查找23。从根开始，因为23<35，则顺该节点中指针A0找到*b节点，又因为*b节点中只有一个关键字18，且23>18，所以顺节点中第二个指针A1找到*e节点。同理因为23<27,则顺指针往下找，此时因指针所指为叶子节点，说明此棵B-树中不存在关键字23,查找失败而告终。

2.1 查找分析

通过上面可知，在B-树上进行查找包含两种基本操作： 1) 在B-树中找节点； 2) 在节点中找关键字。由于B-树通常存储在磁盘上，则前一查找操作是在磁盘上进行的，而后一查找操作是在内存中进行的，即在磁盘上找到指针p所指节点后，先将节点中的信息读入内存，然后再利用顺序查找或者折半查找查询等于K的关键字。显然，在磁盘上进行一次查找比在内存中进行一次查找耗费时间多得多，因此，在磁盘上进行查找的次数、即待查关键字所在节点在B-树上的层次数，是决定B-树查找效率的首要因素。

现考虑最坏的情况，即待查节点在B-树上的最大层次数。也就是，含有N个关键字的m阶B-树的最大深度是多少？我们先看一棵3阶B-树。按B-树的定义，3阶的B-树上所有非终端节点至多可以有两个关键字，至少有一个关键字（即子树个数为2或3，故又称为2-3树)。因此，若关键字个数<=2时，树的深度为2（即nil叶子节点层次为2）；若关键字个数<=6时，树的深度不超过3。反之，若B-树的深度为4，则关键字个数必须>=7。此时，每个节点都含有可能的关键字的最小数目：

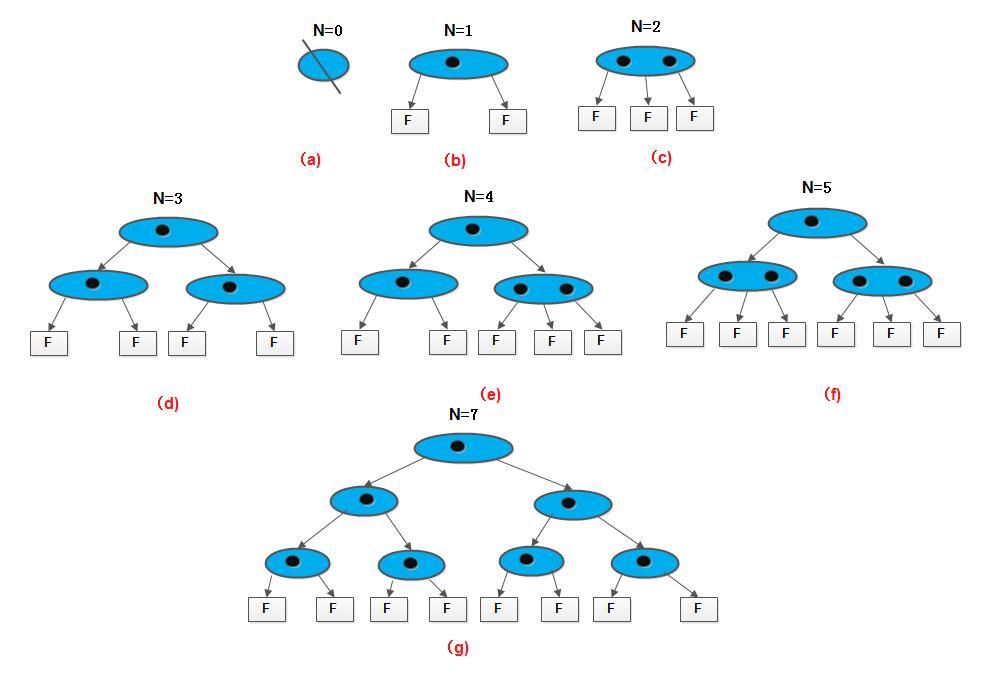
ds-btree-search

一般情况的分析可类似二叉平衡树进行，先讨论深度为l+1的m阶B-树所具有的最少节点数。根据B-树的定义，第一层至少有一个节点；第二层至少有2个节点；由于除根之外的每个非终端节点至少有⌈m/2⌉棵子树，则第三层至少有2⌈m/2⌉个节点， ……，依次类推，第l+1层至少有2⌈m/2⌉^(l-1)个节点。而l+1层的节点为叶子节点。若m阶B-树中具有N个关键字，则叶子节点即查找不成功的节点为N+1，由此有：

         N+1 >= 2⌈m/2⌉^(l-1)

因此可求得l<= log_(⌈m/2⌉)⁡〖(N+1)/2〗 + 1。这就是说，在含有N个关键字的B-树上进行查找时，从根节点到关键字所在节点的路径上涉及的节点数不超过log_(⌈m/2⌉)⁡〖(N+1)/2〗 + 1。

3. B-树的插入

其实B-树的插入是很简单的，它主要分为如下两个步骤：

1）使用之前介绍的查找算法查找出关键字的插入位置，如果我们在B-树中查找到了关键字，则直接返回；否则它一定会失败在某个最低层的终端节点上

2）然后，我们就需要判断那个终端节点上的关键字是否满足n<=m-1, 如果满足的话，就直接在该终端节点上添加一个关键字，否则我们就需要产生节点的分裂。

节点分裂的方法是：生成一个新节点。然后把原节点上的关键字和k(需要插入的值)按升序排列，从中间位置把关键字分成左右两个部分(形成3个部分：左半部分、中间关键字、右半部分)。再接着把左半部分所含关键字放在旧节点中，右半部分所含关键字放在新节点中，中间位置的关键字连同新节点的地址插入到父节点中。如果父节点的关键字个数也超过m-1，则要再分裂，再往上插入，直至这个过程传到根节点为止。

下面我们举个例子进行说明。这里假设这棵B-树的阶为3，树在初始化时如下：

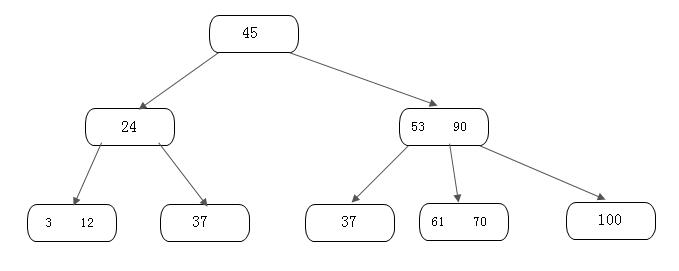
ds-btree-insert0

首先，我们需要插入一个关键字30，可以得到如下结果：

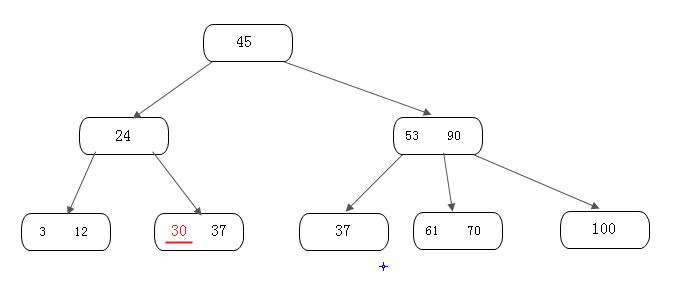
ds-btree-insert1

再插入26，得到如下结果：

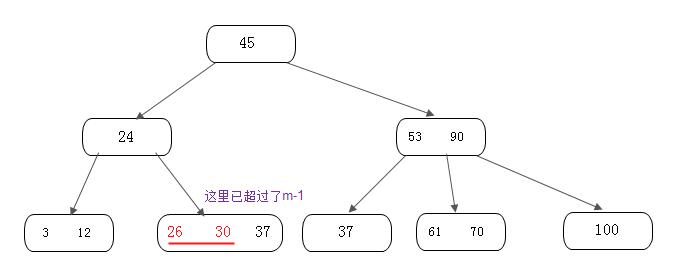
ds-btree-insert2

如上所示，在插入的那个终端节点中，它的关键字数已经超过了m-1，所以我们需要对节点进行分裂。我们先对关键字进行排序，得到：26 30 37，它的左半部分为 26，中间值为30，右半部分是37。然后我们将左半部分放在原来的节点，右半部分放在新的节点，而中间值则插入到父节点，并且父节点会产生一个新的指针，指向新的节点位置，如下图所示：

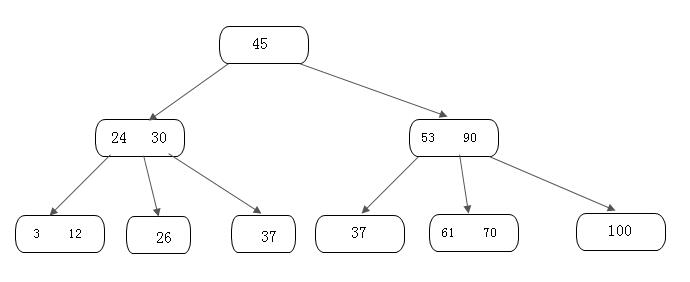
ds-btree-insert3

4. B-树的删除

B-树的删除操作同样分为两个步骤：

1) 利用前述的B-树的查找算法找出该关键字所在的节点，如果没有找到，直接返回；否则根据k(需要删除的关键字)所在的节点是否为叶子节点有不同的处理方法;

2) 若该节点为非叶子节点，且被删关键字为该节点中第i个关键字key[i]，则可以从指针children[i]中找出最小关键字Y, 代替key[i]的位置，然后在叶节点中删去Y;

如果是叶子节点的话，需要分为下面3种情况进行删除：

如果被删关键字所在的节点的原关键字个数n >= ⌈m/2⌉, 说明删去该关键字后该节点仍满足B-树的定义。这种情况最为简单，只需要删除对应的关键字K和指针A即可。

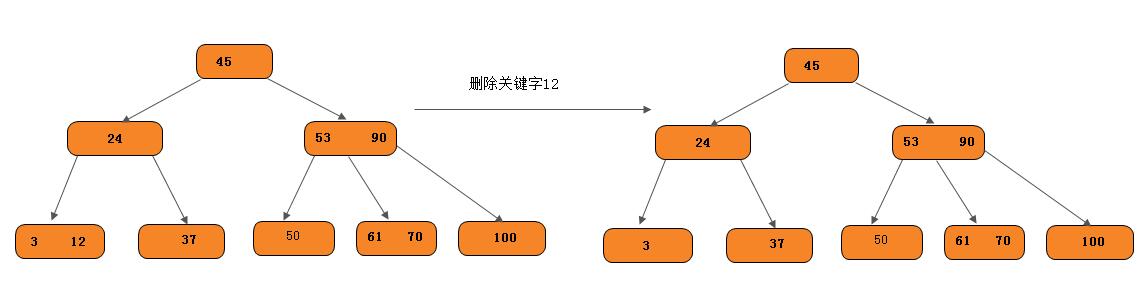
ds-btree-delete1

如果被删关键字所在节点的关键字个数n等于⌈m/2⌉-1, 而与该节点相邻的右兄弟（或左兄弟）节点中关键字数目大于⌈m/2⌉-1,则需将其兄弟节点中最小（或最大）的关键字上移至双亲节点，而将双亲节点中小于（或大于）且紧靠该上移关键字的关键字下移至被删关键字所在的节点中。

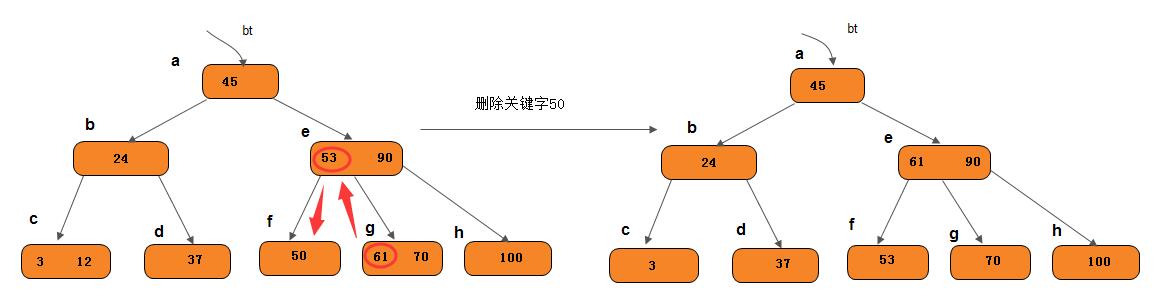
ds-btree-delete2

我们从上图中删除关键字50，需将其右兄弟节点中的61上移至*e节点中，而将*e节点中的53移至*f，从而使*f和*g中关键字数目均不小于⌈m/2⌉-1，而双亲节点中关键字数目不变。

被删关键字所在节点和其相邻的兄弟节点中的关键字数目均等于⌈m/2⌉-1。假设该节点有右兄弟，且其右兄弟节点地址由双亲节点中的指针Ai所指，则在删去关键字之后，它所在节点中剩余的关键字和指针，加上双亲节点中的关键字Ki一起，合并到Ai所指的兄弟节点中（若没有右兄弟，则合并至左兄弟节点中）。

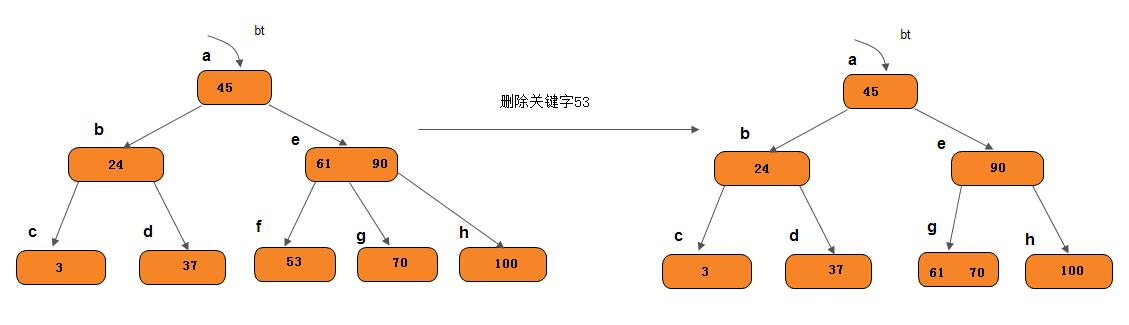
ds-btree-delete31

从上图所示B-树中删去53，则应删去*f节点，并将*f中剩余信息（指针“空”)和双亲节点*e节点中的61一起合并到右兄弟节点*g中。如果因此使双亲节点中的关键字数目小于⌈m/2⌉-1，则依次类推作相应处理。如下图所示：

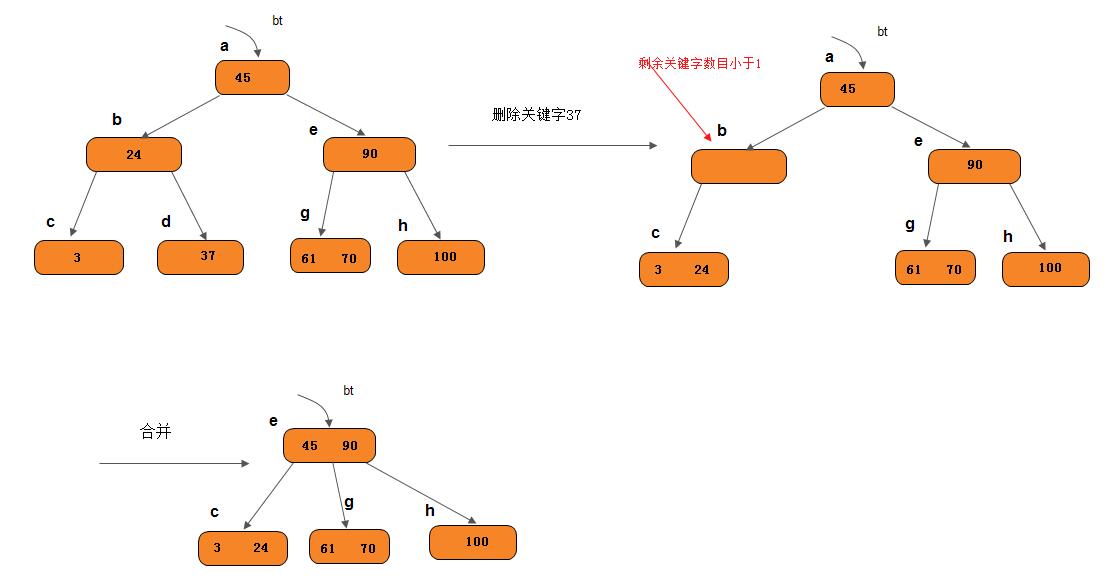
ds-btree-delete32

如上B-树中删去关键字37之后，双亲b节点中剩余信息（“指针”c）应和其双亲*a节点中关键字45一起合并到右兄弟节点*e中。

5. 相关代码参考

5.1 B-树头文件

如下是B-tree头文件btree.h:

#ifndef __BTREE_H_
#define __BTREE_H_



typedef struct bnode_t{
	int key_number;
	int *keys;					//Note: here keys[0] not use
	struct bnode_t **children;
	struct bnode_t *parent;
}BNode;

typedef struct btree_t{
	int m;

	BNode *root;
}BTree;



BTree * create_btree(int m);


void tranverse(BTree *btree);

#endif

5.2 实现文件

如下是B-tree实现源代码文件btree.c:

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "btree.h"


struct TmpBNode{
	int key;
	struct bnode_t *child;
};

BTree * create_btree(int m)
{
	BTree *btree = (BTree *)malloc(sizeof(BTree));
	btree->m = m;
	btree->root = NULL;

	return btree;
}

static BNode *create_bnode(int m)
{
	BNode *bnode = (BNode *)malloc(sizeof(BNode));
	if(!bnode)
		return NULL;

	bnode->keys = (int *)malloc(sizeof(int) * m);
	bnode->children = (BNode **)malloc(sizeof(BNode *) * m);
	if(!bnode->keys || !bnode->children)
	{
		free(bnode->keys);
		free(bnode->children);
		free(bnode);
		return NULL;
	}

	bnode->key_number = 0;
	bnode->parent = NULL;
	memset(bnode->keys, 0x0, sizeof(int) * m);
	memset(bnode->children, 0x0, sizeof(BNode *)*m);
	return bnode;

}


static int insert_combine_node(BTree *btree, BNode *node, struct TmpBNode *tmpNode)
{
	int i,j, insert_pos, middle;
	int right_cnt;
	int flag;

	if(node->key_number < btree->m-1)
	{

		//directly combine
		insert_pos = node->key_number + 1;

		for(i = node->key_number; i>=1;i--)
		{
			if(tmpNode->key > node->keys[i])
				break;
			else{
				node->keys[i+1] = node->keys[i];
				node->children[i+1] = node->children[i];
				insert_pos--;
			}
		}

		node->keys[insert_pos] = tmpNode->key;
		node->children[insert_pos] = tmpNode->child;
		if(tmpNode->child)
			tmpNode->child->parent = node;

		node->key_number = node->key_number + 1;
		return 0x0;

	}

	BNode *newNode = create_bnode(btree->m);
	if(!newNode)
		return -1;


	//calc middle	
	middle = (node->key_number + 1 + 1)/2;
	right_cnt = node->key_number + 1 - middle;
	newNode->key_number = right_cnt;


	flag = 0;
	i = node->key_number;
	while(right_cnt)
	{
		if(!flag && tmpNode->key > node->keys[i])
		{
			newNode->keys[right_cnt] = tmpNode->key;
			newNode->children[right_cnt] = tmpNode->child;
			if(tmpNode->child)
				tmpNode->child->parent = newNode;

			flag = 1;
			right_cnt--;
		}
		else{
			newNode->keys[right_cnt] = node->keys[i];
			newNode->children[right_cnt] = node->children[i];
			right_cnt--;
			i--;
		}
	}

	if(!flag)
	{
		insert_pos = i+1;

		for(i; i>=1;i--)
		{
			if(tmpNode->key > node->keys[i])
				break;
			else{
				node->keys[i+1] = node->keys[i];
				node->children[i+1] = node->children[i];
				insert_pos--;
			}
		}

		node->keys[insert_pos] = tmpNode->key;
		node->children[insert_pos] = tmpNode->child;
		if(tmpNode->child)
			tmpNode->child->parent = node;

	}

	newNode->children[0] = node->children[middle];
	tmpNode->key = node->keys[middle];
	tmpNode->child = newNode;
	node->key_number = middle-1;

	if(node->parent)
	{
		return insert_combine_node(btree, node->parent, tmpNode);
	}
	else{
		BNode * root = create_bnode(btree->m);
		if(!root)
			return -1;
		root->parent = NULL;
		root->key_number = 1;
		root->keys[1] = tmpNode->key;
		root->children[0] = node;
		root->children[1] = tmpNode->child;
		node->parent = root;
		if(tmpNode->child)
			tmpNode->child->parent = root;

		btree->root = root;

		return 0x0;
	}
}

int insert_btree(BTree *btree, int key)
{
	BNode *p = btree->root;
	BNode *q = NULL;
	int i;

	while(p)
	{
		for(i = 0;i<p->key_number;i++)
		{
			if(p->keys[i+1] == key)
				return -1;
			else if(p->keys[i+1] > key)
				break;

		}
		q = p;
		p = p->children[i];
	}
	if(!q)
	{
		btree->root = (BNode *)malloc(sizeof(BNode));
		if(!btree->root)
			return -1;

		BNode *newNode = create_bnode(btree->m);
		if(!newNode)
			return -1;

		newNode->key_number = 1;
		newNode->keys[1] = key;
		newNode->children[0] = newNode->children[1] = NULL;
		newNode->parent = NULL;
		btree->root = newNode;

		return 0x0;

	}

	struct TmpBNode tmpNode;
	tmpNode.key = key;
	tmpNode.child = NULL;

	return insert_combine_node(btree, q, &tmpNode);

}

static void inorder_tranverse(BNode *node)
{
	int i = 0;
	if(!node)
		return;

	for(i = 0;i<= node->key_number; i++)
	{
		inorder_tranverse(node->children[i]);

		if(i < node->key_number)
			printf("%d ", node->keys[i+1]);
	}


}
void tranverse(BTree *btree)
{
	inorder_tranverse(btree->root);
}

5.3 测试

如下是测试源文件main.c:

#include <stdio.h>
#include <stdlib.h>
#include "btree.h"


int main(int argc,char *argv[])
{
	BTree *btree = create_btree(5);

	if(!btree)
	{
		printf("create btree failure\n");
		return -1;
	}

	int a[] = {200, 10, 400, 20, 80, 150, 350, 1000, 250, 180, 220, 500, 650};
	int i = 0;

	for(i = 0;i<sizeof(a)/sizeof(int);i++)
	{
		if(insert_btree(btree, a[i]) != 0)
		{
			printf("insert '%d' failure\n", a[i]);
			return -1;
		}
	}

	printf("inorder tranverse: \n");
	tranverse(btree);
	printf("\n");
	return 0x0;

}

编译运行：

# gcc -o btree *.c
# ./btree
inorder tranverse: 
10 20 80 150 180 250 350 200 220 400 500 650 1000

[参看]:

Ivanzz

发上等愿，结中等缘，享下等福；择高处立，寻平处住，向宽处行