最短路径
本节我们介绍一下如何在一个图中求最短路径。
1. 最短路径
假若要在计算机上建立一个交通咨询系统,则可以采用图的结构来表示实际的交通网络。如下图7.33所示,图中顶点表示城市,边表示城市间的交通联系。这个咨询系统可以回答旅客提出的各种问题。例如,一位旅客要从A城到B城,他希望选择一条途中中转次数最少的路线。假设图中每一站都需要换车,则这个问题反映到图上就是要找一条从顶点A到B所含边的数目最少的路径。
我们只需从顶点A出发对图作广度优先搜索,一旦遇到B就终止。由此所得广度优先生成树上,从根顶点A到顶点B的路径就是中转次数最少的路径,路径上A与B之间的顶点就是途径的中转站数,但是,这只是一类最简单的图的最短路径问题。有时,对于旅客来说,可能更关心的是节省交通费用;而对于司机来说,里程和速度则是他们感兴趣的信息。为了在图上表示有关信息,可对边赋予权,权的值表示两城市间的距离,或途中所需时间,或交通费用等等。此时路径长度的度量就不再是路径上边的数目,而是路径上边的权值之和。考虑到交通图的有向性(如航运,逆水和顺水时的船速就不一样),本节将讨论带权有向图,并称路径上的第一个顶点为源点(Source),最后一个顶点为终点(Destination)。下面讨论两种最常见的最短路径问题。
1.1 从某个源点到其余各顶点的最短路径
我们先来讨论单源点的最短路径问题:给定带权有向图G和源点v,求v到G中其余各顶点的最短路径。
例如,图7.34所示带权有向图G6中从v0到其余各定点之间的最短路径,如图7.35所示。从图中可见,从v0到v3有两条不同的路径: (v0,v2,v3)和(v0,v4,v3),前者长度为60,而后者长度为50。因此,后者是从v0到v3的最短路径;而从v0到v1没有路径。
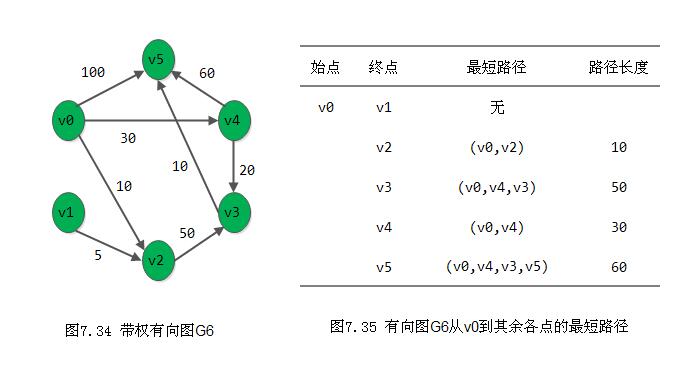
如何求得这些路径?迪杰斯特拉(Dijkstra)提出了一个按路径长度递增的次序产生最短路径的算法。
首先,引进一个辅助向量D,它的每个分量D[i]表示当前所找到的从始点v到每个终点vi的最短路径的长度。它的初态为:若从v到vi有弧,则D[i]为弧上的权值;否则置D[i]为∞。显然,长度为
D[j] = Min{D[i] | vi ∈ V}
i
的路径就是从v出发的长度最短的一条最短路径。此路径为(v,vj)。
那么,下一条长度次短的最短路径是哪一条呢?假设该次短路径的终点是vk,则可想而知,这条路径或者是(v,vk),或者是(v,vj,vk)。它的长度或者是从v到vk的弧上的权值,或者是D[j]和从vj到vk的弧上额权值之和。
一般情况下,假设S为已求得最短路径的终点的集合,则可以证明:下一条最短路径(设其终点为x)或者是弧(v,x),或者是中间只经过S中的顶点而最后到达顶x的路径。这可以用反证法来证明。假设此路径上有一个顶点不在S中,则说明存在一条终点不在S而长度比此路径短的路径。但是,这是不可能的。因为我们是按照路径长度递增的次序来产生各最短路径的,故长度比此路径短的所有路径均已产生,它们的终点必定在S中,即此假设不成立。
因此,在一般情况下,下一条长度次短的最短路径长度必是:
D[j] = Min{D[i] | vi ∈ V-S}
i
其中,D[i]或者是弧(v,vi)上的权值,或者是D[k](vk ∈ S)和弧(vk,vi)上的权值之和。
根据以上分析,可以得到如下描述的算法:
1) 假设使用带权的邻接矩阵arcs来表示带权有向图,arcs[i][j]表示弧<vi,vj>上的权值。若<vi,vj>不存在,则置arcs[i][j]为∞(在计算机上可用允许的最大值代替)。S为已找到从v出发的最短路径的终点的集合,它的初始状态为空集。那么从v出发到图上其余各定点(终点)vi可能达到的最短路径长度的初值为:
D[i] = arcs[LocateVex(G,v)][i] vi ∈ V
2) 选择vj,使得
D[j] = Min{D[i] | vi ∈ V-S}
vj就是当前求得的一条从v出发的最短路径的终点。令
S = S U {j}
3) 修改从v出发到集合V-S上任一顶点vk可达的最短路径长度。如果
D[j] + arcs[j][k] < D[k]则修改D[k]为
D[k] = D[j] + arcs[j][k]
4) 重复操作2)、3)共n-1次,由此求得从v到图上其余各顶点的最短路径是依路径长度递增的序列。
算法7.15为用C语言描述的迪杰斯特拉算法:
void ShortestPath_DIJ(MGraph G, int v0, PathMartix &P, ShortPathTable &D)
{
//用Dijkstra算法求有向网G的v0顶点到其余顶点v的最短路径P[v]及其带权路径长度D[v]
//若P[v][w]为TRUE,则w是从v0到v当前求得最短路径上的顶点
//final[v]为TRUE当且仅当v∈S,即已经求得v0到v的最短路径
for(v = 0; v < G.vexnum; ++v){
final[v] = FALSE;
D[v] = G.arcs[v0][v];
for(w = 0; w < G.vexnum; ++w){
P[v][w] = FALSE; //设空路径
}
if(D[v] < INFINITY){
P[v][v0] = TRUE;
P[v][v] = TRUE;
}
}
D[v0] = 0; final[v0] = TRUE; //初始化,v0顶点属于S集
/*
*开始主循环,每次求得v0到某个v顶点的最短路径,并加v到S集
*/
for(i = 1;i<G.vexnum; ++i){ //其余G.vexnum-1个顶点
min = INFINITY; //当前所知离v0顶点的最近距离
for(w = 0; w < G.vexnum; ++w){
if(!final[w]){ //w顶点在V-S中
if(D[w] < min){
v = w;
min = D[w]; //w顶点离v0更近
}
}
}
final[v] = TRUE; //离v0顶点最近的v加入S集
for(w = 0; w < G.vexnum; ++w){ //更新当前最短路径及距离
if(!final[w] && (min + G.arcs[v][w]) < D[w]){ //修改D[w]和P[w], w ∈ V-S
D[w] = min + G.arcs[v][w];
P[w] = P[v];
P[w][w] = TRUE; //P[w] = P[v] + [w]
}
}
}
}例如,图7.34所示有向网G6的带权邻接矩阵为:
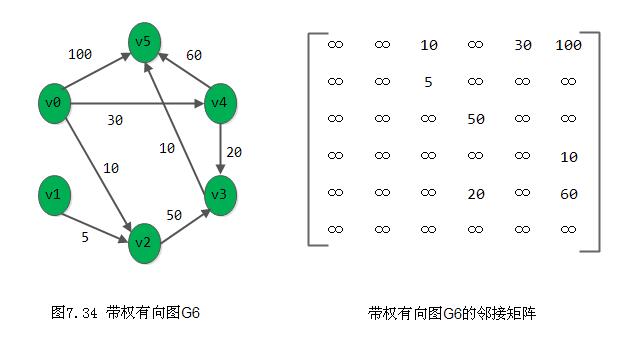
若对G6施行迪杰斯特拉算法,则所得从v0到其余顶点的最短路径,以及运算过程中D向量的变化状况,如下所示:
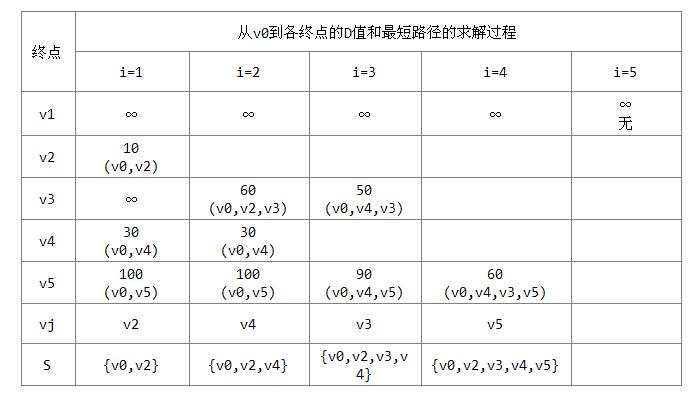
我们分析这个算法的运行时间。第一个FOR循环的时间复杂度是O(n),第二个FOR循环共进行n-1次,每次执行的时间是O(n)。所以总的时间复杂度是O(n^2)。如果用带权的邻接表作为有向图的存储结构,则虽然修改D的时间可以减少,但由于在D向量中选择最小分量的时间不变,所以总的时间复杂度仍为O(n^2)。
人们可能只希望找到从源点到某一特定的终点的最短路径,但是,这个问题和求源点到其他所有顶点的最短路径一样复杂,其时间复杂度也是O(n^2)。
1.2 每一对顶点之间的最短路径
解决这个问题的一个办法是:每次以一个顶点为源点,重复执行迪杰斯特拉算法n次。这样,便可求得每一对顶点之间的最短路径。总的执行时间为O(n^3)。
这里要介绍由弗洛伊德(Floyd)提出的另一个算法。这个算法的时间复杂度也是O(n^3),但形式上简单些。
弗洛伊德算法仍从图的带权邻接矩阵cost出发,其基本思想是:
假设求从顶点vi到vj的最短路径。如果从vi到vj有弧,则从vi到vj存在一条长度为arcs[i][j]的路径,该路径不一定是最短路径,尚需进行n次试探。首先考虑路径(vi,v0,vj)是否存在(即判别弧(vi,v0)和(v0,vj)是否存在)。如果存在,则比较(vi,vj)和(vi,v0,vj)的路径长度,取长度较短者为从vi到vj的中间顶点的序号不大于0的最短路径。假如在路径上再增加一个顶点v1,也就是说如果(vi, …, v1)和(v1, …, vj)分别是当前找到的中间顶点的序号不大于0的最短路径,那么(vi,…, v1, …, vj)就可能是从vi到vj的中间顶点的序号不大于1的最短路径。将它和已经得到的从vi到vj中间顶点序号不大于0的最短路径相比较,从中选出中间顶点的序号不大于1的最短路径之后,再增加一个顶点v2,继续进行试探。依次类推。在一般情况下,若(vi, …, vk)和(vk, …, vj)分别是从vi到vk和从vk到vj的中间顶点的序号不大于k-1的最短路径,则将(vi, …, vk, …, vj)和已经得到的从vi到vj且中间顶点序号不大于k-1的最短路径相比较,其长度较短者便是从vi到vj的中间顶点的序号不大于k的最短路径。这样,在经过n次比较后,最后求得的必是从vi到vj的最短路径。按此方法,可以同时求得各对顶点间的最短路径。

由此,可得算法7.16:
void ShortestPath_FLOYD(MGraph G, PathMatrix &P[], DistanceMatrix &D)
{
//用Floyd算法求有向网G中各对顶点v和w之间的最短路径P[v][w]及其带权长度D[v][w]。
//若P[v][w][u]为TRUE,则u是从v到w当前求得最短路径上的顶点。
for(v = 0; v < G.vexnum; ++v){ //各对节点之间初始已知路径及距离
for(w = 0; w < G.vexnum; ++w){
D[v][w] = G.arcs[v][w];
for(u = 0; u < G.vexnum; ++u){
P[v][w][u] = FALSE;
}
if(D[v][w] < INFINITY){ //从v到w有直接路径
P[v][w][v] = TRUE;
P[v][w][w] = TRUE;
}
}
}
for(u = 0; u < G.vexnum; ++u){ //在路径上插入顶点u时
for(v = 0; v < G.vexnum; ++v){
for(w = 0; w < G.vexnum; ++w){
if(D[v][u] + D[u][w] < D[v][w]){ //从v经u到w的一条路径更短
D[v][w] = D[v][u] + D[u][w];
for(i = 0; i < G.vexnum; ++i)
P[v][w][i] = P[v][u][i] || P[u][w][i];
}
}
}
}
}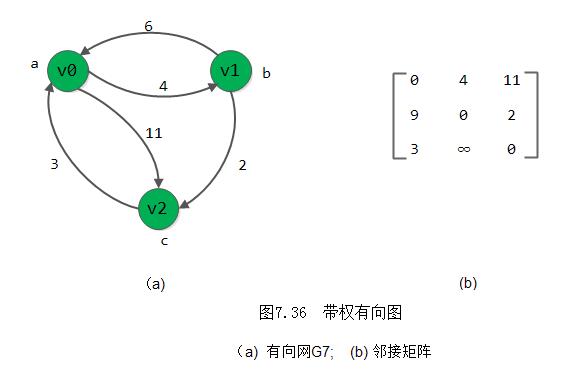
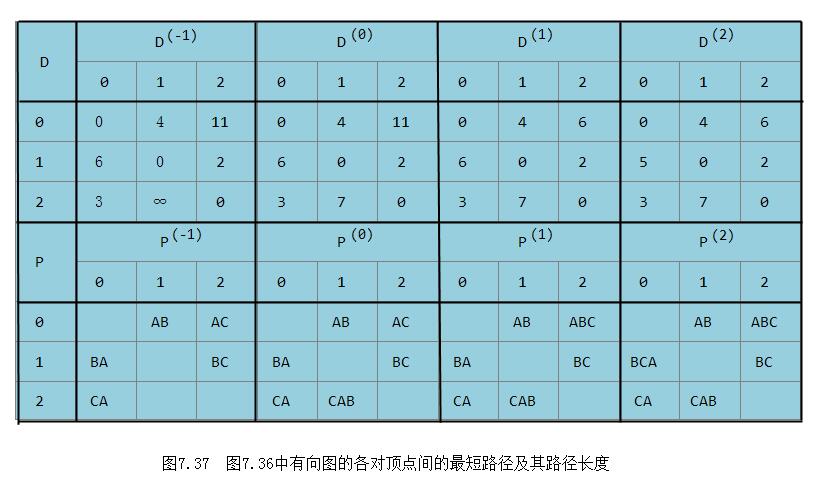
例如,利用上述算法,可求得图7.36所示带权有向图G7的每一对顶点之间的最短路径及其路径长度如图7.37所示。
[参看]:

