哈希表
本文我们主要讲述一下Hash表的基本理论。
1. 哈希表
根据设定的哈希函数H(key)和处理冲突的方法将一组关键字映像到一个有限的连续的地址集(区间)上,并以关键字在地址集中的像作为记录在表中的存储位置,这种表便称为哈希表。这一映像过程称为哈希造表或散列,所得存储位置称为哈希地址或散列地址。
1.1 哈希函数的构造方法
构造哈希函数的方法很多。在介绍各种方法之前,首先需要明确什么是好的哈希函数。若对于关键字集合中任一个关键字,经哈希函数映像到地址集合中任何一个地址的概率是相等的,则称此类哈希函数为均匀的(uniform)哈希函数。换句话说,就是使关键字经过哈希函数得到一个随机的地址,以便使一组关键字的哈希地址均匀分布在整个地址区间中,从而减少冲突。
常用的构造哈希函数的方法有:
-
直接定址法: 取关键字或关键字的某个线性函数值为哈希地址。注: 由于直接定址所得地址集合和关键字集合的大小相同。因此,对于不同的关键字不会发生冲突。但实际中能使用这种哈希函数的情况很少.
-
数字分析法: 假设关键字是以
r为基的数(如: 以10为基的十进制数),并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。 -
平方取中法: 取关键字平方后的中间几位为哈希地址
-
折叠法: 将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址,这种方法称为折叠法(folding)。
-
除留余数法: 取关键字被某个不大于哈希表表长
m的数p除后所得余数为哈希地址。即:
H(key) = key MOD p, p<=m
这是一种最简单,也是最常用的构造哈希函数的方法。它不仅可以对关键字直接取模,也可在折叠、平方取中等运算后取模。
- 随机数法: 选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key) = random(key),其中
random为随机函数。通常,当关键字长度不等时采用此法构造哈希函数较恰当。
实际工作中,需视不同的情况采用不同的哈希函数。通常,考虑的因素有:
-
计算哈希函数所需时间(包括硬件指令的因素)
-
关键字的长度
-
哈希表的大小
-
关键字的分布情况
-
记录的查找频率
1.2 处理冲突的方法
在前面我们提及均匀的哈希函数可以减少冲突,但不能避免,因此如何处理冲突是哈希造表不可缺少的另一方面。假设哈希表的地址集为0~(n-1),冲突是指由关键字得到的哈希地址为 j(0<=j<=n-1)的位置上已存有记录,则处理冲突就是为该关键字的记录找到另一个空的哈希地址。在处理冲突的过程中可能得到一个地址序列Hii=1,2,…k (Hi∈[0,n-1])。即在处理哈希地址冲突时,若得到另一个哈希地址H1仍然发生冲突,则再求下一个H2,若H2仍然冲突,再求H3。依次类推,直至Hk不发生冲突为止。则Hk为记录在表中的地址。
通常用的处理冲突的方法有下列几种:
1) 开放定址法
Hi = (H(key) + di) MOD m i=1,2,...k (k<=m-1)其中: H(key)为哈希函数; m为哈希表表长; di为增量序列,可有下列三种取法:
-
di=1,2,3…m-1, 称为线性探测再散列
-
di=1^2, -1^2, 2^2, -2^2,…, k^2, -k^2(k<=m/2),称为二次探测再散列
-
di=伪随机数序列,称为伪随机探测再散列
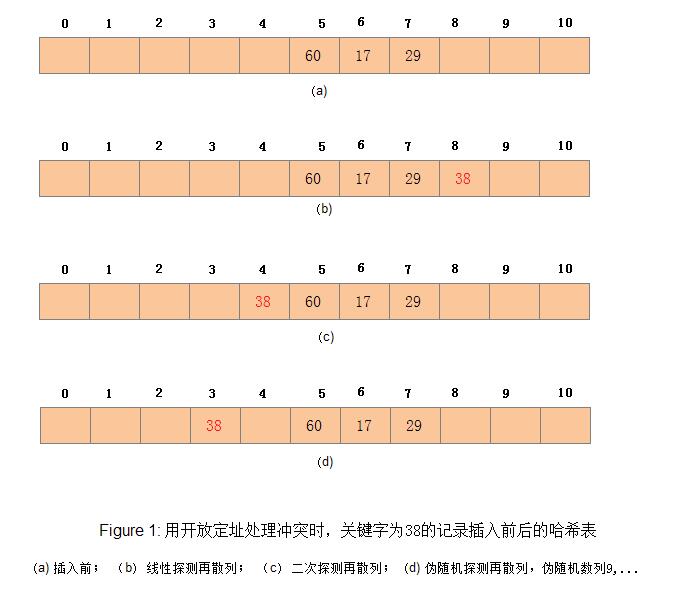
例如,在长度为11的哈希表中已填有关键字分别为17,60,29的记录(哈希函数H(key)=key MOD 11),现有第四个记录,其关键字为38,由哈希函数得到哈希地址为5,产生冲突。若用线性探测再散列的方法处理时,得到下一个地址6,仍冲突; 再求下一个地址7,仍冲突;直到哈希地址为8的位置为“空”时止,处理冲突的过程结束,记录填入哈希表中序号为8的位置。若用二次探测再散列,则应该填入序号为4的位置。类似地可得到伪随机再散列地址。
从上述线性探测再散列的过程中可以看到一个现象: 当表中i, i+1, i+2位置上已填有记录时,下一个哈希地址为i, i+1, i+2和i+3的记录都将填入i+3的位置,这种在处理冲突过程中发生的两个第一个哈希地址不同的记录争夺同一个后继哈希地址的现象称作二次聚集,即在处理同义词的冲突过程中又添加了非同义词的冲突,显然,这种现象对查找不利。但另一方面,用线性探测再散列处理冲突可以保证做到: 只要哈希表未填满,总能找到一个不发生冲突的地址Hk;而二次探测再散列只有在哈希表长m为形如4j+3(j为整数)的素数时才可能;随机探测再散列,取决于伪随机数列。
2)再哈希法
Hi = RHi(key) i=1,2,3...,k
其中,RHi均是不同的哈希函数,即在同义词产生地址冲突时,计算另一个哈希函数地址,直到冲突不再发生。这种方法不易产生聚集,但增加了计算的时间。
3) 链地址法
将所有关键字为同义词的记录存储在同一线性链表中。假设某哈希函数产生的哈希地址在区间[0,m-1]上,则设立一个指针型向量Chain ChainHash[m],其每个分量的初始状态都是空指针。凡哈希地址为i的记录都插入到头指针为ChainHash[i]的链表中。在链表的插入位置可以在表头或表尾; 也可以在中间,以保持同义词在同一线性链表中按关键字有序。
4) 建立一个公共溢出区
这也是处理冲突的一种方法。假设哈希函数的值域为[0,m-1],则向量HashTable[0..m-1]为基本表,每个分量存放一个记录,另设立向量OverTable[0..v]为溢出表。所有关键字和基本表中关键字为同义词的记录,不管它们由哈希函数得到的哈希地址是什么,一旦发送冲突,都填入溢出表。
2. 哈希表的查找
在哈希表上进行查找的过程和哈希造表的过程基本一致。给定K值,根据造表时设定的哈希函数求得哈希地址, 若表中此位置上没有记录,则查找不成功;否则比较关键字,若和给定的值相等,则查找成功;否认根据造表时设定的处理冲突的方法找下一地址,直至哈希表中某个位置为“空”或者表中所填记录的关键字等于给定值时为止。

