内部排序(上)
本节我们介绍一下计算机中各种常用的内部排序算法。
1. 内部排序
排序(sorting)是计算机程序设计中的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个按关键字有序的序列。
内部排序的方法很多,但就其全面性能而言,很难提出一种被认为是最好的方法,每一种方法都有各自的优缺点,适合在不同的环境(如记录的初始排列状态等)下使用。如果按排序过程中依据的不同原则对内部排序方法进行分类,则大致可以分为如下5类:
-
插入排序
-
交换排序
-
选择排序
-
归并排序
-
计数排序
如果按内部排序过程中所需的工作量来区分,则可以分为如下3类:
-
简单排序方法: 其时间复杂度为O(n^2)
-
先进的排序方法: 其时间复杂度为O(nlogn)
-
基数排序: 其时间复杂度为O(d*n)
2. 插入排序
插入排序又可以分为多种。下面我们简单介绍。
2.1 直接插入排序
直接插入排序(Straight Insertion Sort)是一种最简单的排序方法,它的基本操作是将一个记录插入到已排好序的有序表中,从而得到一个新的、记录数增1的有序表。
一般情况下,第i趟直接插入排序的操作为: 在含有i-1个记录的有序子序列r[1..i-1]中插入一个记录r[i],变成含有i个记录的有序子序列r[1..i];并且,和顺序查找类似,为了在查找插入位置的过程中避免数组下标出界,在r[0]处设置监视哨。在自i-1起往前搜索的过程中,可以同时后移记录。整个排序过程为进行n-1趟插入,即: 先将序列中的第一个记录看成是一个有序的子序列,然后从第2个记录起逐个进行插入,直至整个序列变成按关键字非递减有序序列为止。
1) 相关算法
下面给出相关算法伪代码:
//use 'Straight Insertion Sort'
void InsertSort(SqList *L)
{
for(i = 2;i<=L->length;i++)
{
if(LT(L->r[i].key, L->r[i-1].key)
{
L->r[0] = L.r[i]; //L->r[0] as the sentinal
L->r[i]= L->r[i-1];
for(j = i-2;LT(L->r[0].key, L->r[j].key); --j)
L->r[j+1] = L->r[j];
L->r[j+1] = L->r[0];
}
}
}2) 时间及空间复杂度
从上面我们可以看到,直接插入排序的算法简洁,容易实现,那么它的效率如何呢?
从空间来看,它只需要一个记录的辅助空间; 从时间来看,排序的基本操作为:比较两个关键字的大小和移动记录。先分析一趟插入排序的情况。在上面的算法中里层for循环的次数取决于待插记录的关键字与前i-1个记录的关键字之间的关系。若L->r[i].key<L->r[1].key,则内循环中,待插记录的关键字需与有序子序列L.r[1..i-1]中i-1个记录的关键字和监视哨中的关键字进行比较,并将L.r[1..i-1]中i-1个记录后移。则在整个排序过程(进行n-1趟插入排序)中,当待排序列中记录按关键字非递减有序排列(称为”正序”)时,所需进行关键字间比较的次数达最小值n-1,记录不需移动; 反之,当待排序列中记录按关键字非递增有序排列(称为“逆序”)时,总的比较次数达到最大值(n+2)(n-1)/2,记录移动的次数也达到最大值(n+4)(n-1)/2。若待排序记录是随机的,即待排序列中的记录可能出现的各种排列的概率相同, 则我们可取上述最小值和最大值的平均值,作为直接插入排时所需进行关键字比较次数和移动记录的次数,约为n^2/4。由此,直接插入排序的时间复杂度为O(n^2)。
2.2 其他插入排序
上面我们看到,直接插入排序算法简便,且容易实现。当待排记录的数量n很小时,这是一种很好的排序方法。但是,通常待排序列中记录数量n很大,则不宜采用直接插入排序。由此,需要讨论改进的办法。在直接插入排序的基础上,从减少比较和移动这两种操作的次数着眼,可得下列各种插入排序方法。
1) 折半插入排序
由于插入排序的基本操作是在一个有序表中进行查找和插入。因此这个查找操作可以利用折半查找来实现,由此进行的插入排序称之为折半插入排序(Binary Insertion Sort)。
void BInsertSort(SqList *L)
{
for(i=2;i<=L->length;i++)
{
L.r[0] = L.r[i];
low = 1, high = i-1;
while(low <= high)
{
m = (low + high) >> 1;
if(LT(L->r[0].key, L->r[m].key))
high = m -1;
else
low = m+1;
}
for(j=i-1;j>=high+1;j--)
L->r[j+1] = L->r[j];
L->r[high+1] = L->r[0];
}
}从上面可以看出,折半插入排序所需附加存储空间和直接插入排序相同,从时间上比较,折半插入排序仅减少了关键字间的比较次数,而记录的移动次数不变。因此,折半插入排序的时间复杂度仍为O(n^2)。
2) 2-路插入排序
2-路插入排序是在折半插入排序的基础上再改进之,其目的是减少排序过程中移动记录的次数,但为此需要n个记录的辅助空间。具体做法是:另设一个和L.r同类型的数组d,首先将L.r[1]赋值给d[1],并将d[1]看成是在排好序的序列中处于中间位置的记录, 然后从L.r中第2个记录起依次插入到d[1]之前或之后的有序序列中。先将待插记录的关键字和d[1]的关键字进行比较,若L.r[i].key小于d[1].key,则将L.r[i]插入到d[1]之前的有序表中。反之,则将L.r[i]插入到d[1]之后的有序表中。在实现算法时,可将d看成是一个循环向量,并设两个指针first和final分别指示排序过程中得到的有序序列中的第一个和最后一个记录在d中的位置。
void BWInsertSort(SqList *L, SqList *D)
{
int first, last, i;
first = last = 1;
//由于L->r[0]未使用,因此这里我们需要将[first, last]中的数据映射到[1, D->length]位置上
//假设当前下标偏移为n,则映射到[1,D->length]位置的方法为: (n-1 + D->length) % D->length + 1
len = L->length;
D->r[1] = L->r[1];
for(i = 2; i <= L->length; i++){
if(L->r[i] < D->r[1]){
low = first;
high = 1;
while(low <= high){
middle = (low + high) /2;
if(D->r[(middle -1 + len) % len + 1] <= L->r[i]){
low = middle+1;
}else{
high = middle-1;
}
}
for(j = first; j <= low -1; j++)
D->r[((j-1) - 1 + len) % len + 1] = D->r[(j -1 + len) % len + 1];
D->r[((low-1) -1 + len) % len + 1] = L->r[i];
first--;
}else{
low = 1;
high = last;
while(low <= high){
middle = (low + high) >> 1;
if(D->r[(middle -1 + len) % len + 1] <= L->r[i])
low = middle + 1;
else{
high = middle -1;
}
}
for(j = last; j>=high+1; j--){
D->r[((j+1)-1 + len) % len + 1] = D->r[(j -1 + len) % len +1];
}
D->r[((high+1)-1 + len) % len + 1] = L->r[i];
last++;
}
}
}在2-路插入排序中,移动记录的次数约为(n^2)/8。因此,2-路插入排序只能减少移动记录的次数,而不能绝对避免移动记录。并且,当L->r[1]是待排序记录中的最小或最大记录时,2-路插入排序就完全失去它的优越性。因此,若希望在排序过程中不移动记录,只有改变存储结构,进行表插入排序。
3) 表插入排序
#define SIZE 100 //静态链表容量
//表节点类型
typedef struct{
RcdType rc; //记录项
int next; //指针项
}SLNode;
//静态链表类型
typedef struct{
SLNode r[SIZE]; //0号单元为表头节点
int length; //链表当前长度
}SLinkListType;假设以上述说明的静态链表类型作为待排记录序列的存储结构,并且,为了插入方便起见,设数组中下标为0的分量为头节点,并令表头节点记录的关键字取最大整数MAXINT。则表插入排序的过程描述如下: 首先将静态链表中数组下标为1的分量和表头节点构成一个循环链表,然后依次将下标为2至n的分量按记录关键字非递减有序插入到循环链表中。如下图所示:
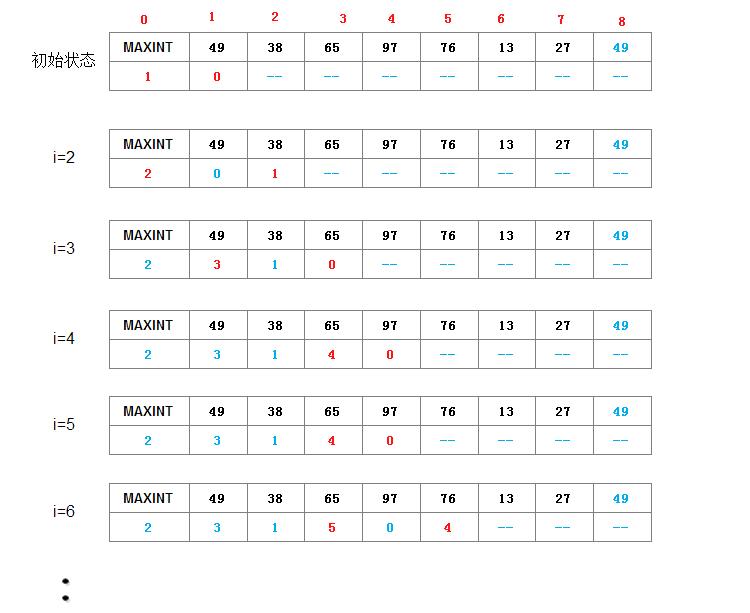
void ListInsertSort(SLinkListType &list)
{
list.r[1].next = 0;
for(i = 2;i<=list.length;i++)
{
current = 0;
while(list.r[current].next)
{
next = list.r[current].next
if(LT(list->r[i].rc,list.r[next].rc))
break;
current = next
}
list.r[i].next = list.r[current].next;
list.r[current].next = i;
}
}从上面表插入排序的过程可见,表插入排序的基本操作仍是将一个记录插入到已排好序的有序表中。和直接插入排序相比,不同之处仅是以修改2n次指针值代替移动记录,排序过程中所需进行的关键字间的比较次数相同。因此,表插入排序的时间复杂度仍是O(n^2)。
另一方面,表插入排序的结果只是求得一个有序链表,则只能对其进行顺序查找,不能进行随机查找,为了能实现有序表的折半查找,尚需对记录进行重新排列。
重排的做法是: 顺序扫描有序链表(6->7->2->1->8->3->5->4),将链表中第i个节点移动至数组的第i个分量中。例如有如下图:
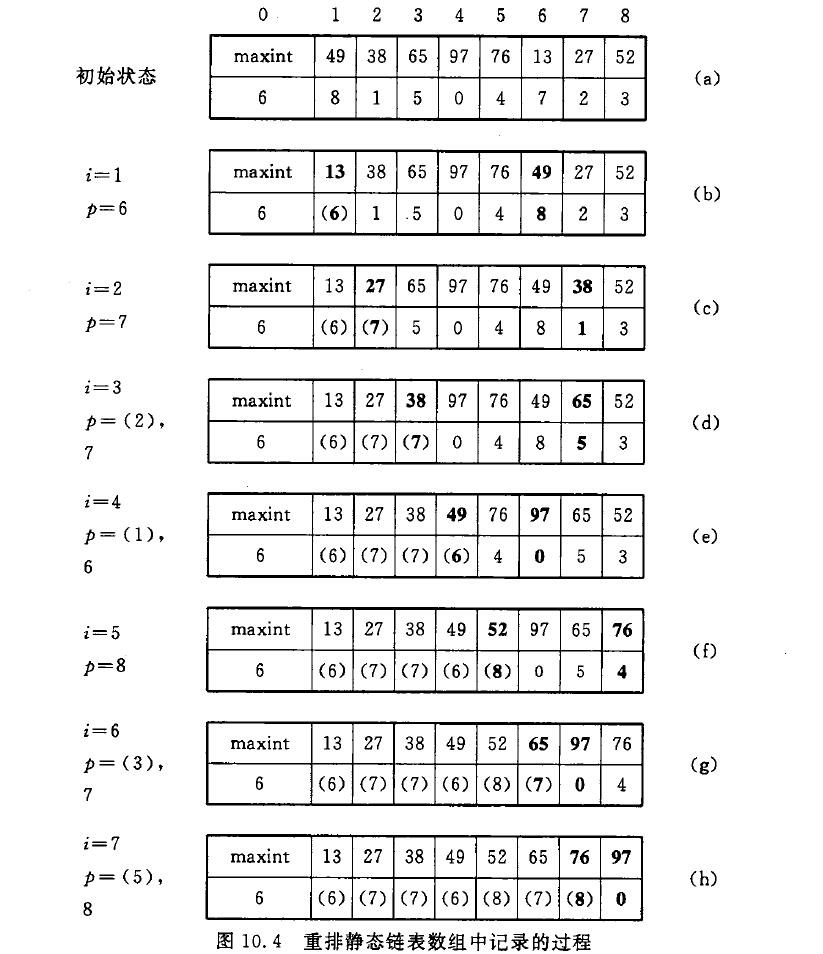
上图是经表插入排序后得到的有序链表SL。根据头节点中指针域的指示,链表的第一个节点,即关键字最小的节点是数组中下标为6的分量,其中记录应移至数组的第一个分量中,则将SL.r[1]和SL.r[6]互换,并且为了不中断静态链表中的“链”, 即在继续顺链扫描时仍能找到之前在SL.r[1]中的节点,令互换之后的SL.r[1]中指针域的值改为“6”(见上图b)。推广至一般情况, 若第i个最小关键字的节点是数组下标为p且p>i的分量,则互换SL.r[i]和SL.r[p],且令SL.r[i]中指针域的值改为p;由于此时数组中所有小于i的分量中已是“到位”的记录,则当p<i时,应顺链继续查找直到p>=i为止。
如下算法描述了上述重排记录的过程。
//根据静态链表SL中各节点的指针值调整记录位置,使得SL中记录按关键字非递减有序顺序排列
void Arrange(SLinkListType &SL)
{
p = SL.r[0].next;
//注意: 这里最后一个SL.length可以不需要调整了
for(i = 1;i<SL.length;i++)
{
while(p < i)
p = SL.r[p].next; //找到第i个记录,并用p指示其在SL中当前位置
q = SL.r[p].next;
if(p != i)
{
tmp = SL.r[i];
SL.r[i] = SL.r[p];
SL.r[p] = tmp;
SL.r[i].next = p;
}
p = q;
}
}容易看出,在重排记录的过程中,最坏情况是每个记录到位都必须经历一次记录的交换,即3次移动记录,所以重排记录至多需进行3(n-1)次记录的移动,它并不增加表插入排序的时间复杂度。
3. 希尔插入排序
3.1 算法描述
希尔排序(Shell’s Sort)又称“缩小增量排序”(Diminishing Increment Sort),它也是一种属插入排序类的方法,但在时间效率上较前述几种排序方法有较大的改进。
从对直接插入排序的分析得知,其算法时间复杂度为O(n^2),但是若待排记录序列为“正序”时,其时间复杂度可提高至O(n)。由此可设想,若待排记录序列按关键字“基本有序”时,直接插入排序的效率就可以大大提高,从另一方面来看,由于直接插入排序算法简单,则在n值很小时效率也比较高。希尔排序正是从这两点出发对直接插入排序进行改进得到的一种插入排序算法。
它的基本思想是: 先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列记录“基本有序”时,再对全体记录进行一次直接插入排序。
如下图所示,我们来看一下希尔排序的过程。初始关键字序列是图中第1行。首先将该序列分成5个子序列:{R1, R6}, {R2, R7}, …, {R5, R10}, 如下图中的第2行至第6行所示,分别对每个子序列进行直接插入排序,排序结果为图中的第7行, 从第1行的初始序列到第7行的序列的过程称为一趟希尔排序。然后进行第二趟希尔排序,即分别对下列3个子序列: {R1,R4,R7,R10}, {R2, R5, R8}和{R3, R6, R9}进行直接插入排序,其结果如图中第11行所示。最后对整个序列进行一趟直接插入排序。至此,整个序列的记录已按关键字非递减有序排列。
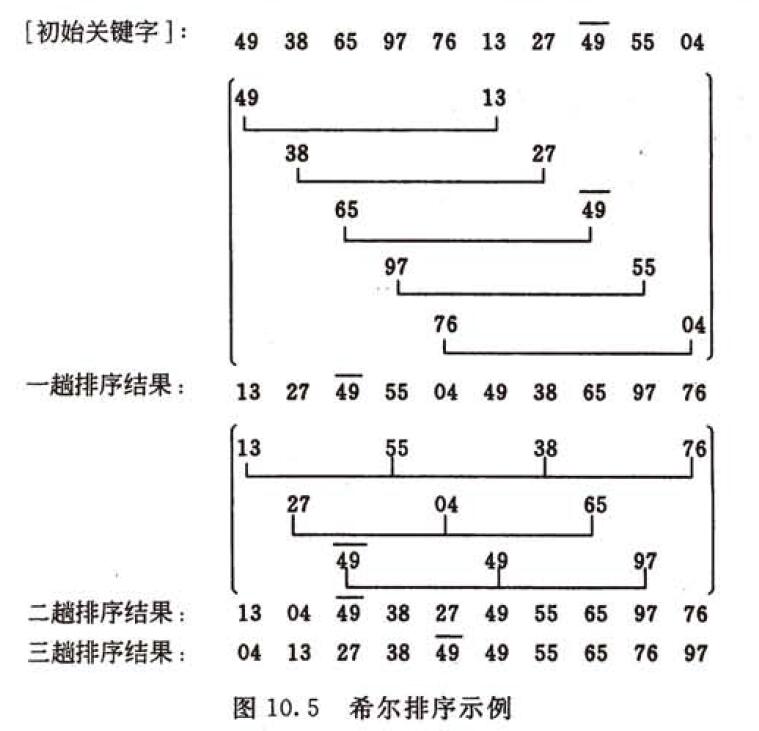
从上述排序过程可见,希尔插入排序的一个特点是: 子序列的构成不是简单地逐段分割,而是将相隔某个增量的记录组成一个子序列。例如上图第一趟排序时的增量是5, 第二趟排序时的增量是3,由于在前两趟的插入排序中记录的关键字是和同一子序列中的前一个记录的关键字进行比较,因此关键较小的记录就不是一步一步地往前挪动,而是跳跃式地往前移,从而使得在进行最后一趟增量为1的插入排序时,序列已基本有序,只要作记录的少量比较和移动即可完成排序,因此希尔排序的时间复杂度较直接插入排序低。一趟希尔插入排序算法如下:
//对顺序表L作一趟希尔插入排序。本算法是和一趟直接插入排序相比,作了以下修改:
// 1) 前后记录位置的增量是dk,而不是1;
// 2) r[0]只是暂存单元,不是哨兵。当j<=0时,插入位置已找到
void ShellInsert(SqList &L, int dk)
{
for(i = dk+1; i<=L.length;i++)
{
if(LT(L.r[i], L.r[i-dk]))
{
L.r[0] = L.r[i];
for(j = i-dk; j > 0 && LT(L.r[0], L.r[j]); j-=dk)
L.r[j+dk] = L.r[j];
L.r[j + dk] = L.r[0];
}
}
}下面是希尔排序算法:
//按增量dlta[0..t-1]对顺序表L作希尔排序
void ShellSort(SqList &L, int dlta[], int t)
{
for(k = 0;k<t;k++)
ShellInsert(L, dlta[k]); //一趟增量为dlta[k]的插入排序
}3.2 希尔插入排序时间复杂度
希尔插入排序的分析是一个复杂的问题,因为它的时间是所取增量序列的函数,这涉及一些数学上尚未解决的难题。因此,到目前为止尚未有人求得一种最好的增量序列, 但大量的研究已得出一些局部结论。如有人指出,当增量序列为dlta=2^(t-k+1) -1时,希尔排序的时间复杂度为O(n^(3/2)),其中t为排序趟数, 1 <= k <= t <= ⌊log2^(n+1)⌋。增量序列有各种取法,但需注意: 应使增量序列中的值没有除1之外的公因子,并且最后一个增量值必须等于1.
最后我们给出希尔排序的另一种写法以作参考:
//对顺序表L作一趟希尔插入排序。本算法是和一趟直接插入排序相比,作了以下修改:
// 1) 前后记录位置的增量是dk,而不是1;
// 2) r[0]只是暂存单元,不是哨兵。当j<=0时,插入位置已找到
void ShellInsert(SqList &L, int dk)
{
for(i = 1; i < dk + 1; i++)
{
for(j = i + dk; j <= L.length; j += dk)
{
if(LT(L.r[j], L.r[j-dk]){
L.r[0] = L.r[j];
for(z = j-dk; z >= 1 && LT(L.r[0], L.r[z]); z -= dk)
L.r[z+dk] = L.r[z];
L.r[z+dk] = L.r[0];
}
}
}
}
//按增量dlta[0..t-1]对顺序表L作希尔排序
void ShellSort(SqList &L, int dlta[], int t)
{
for(k = 0;k<t;k++)
ShellInsert(L, dlta[k]); //一趟增量为dlta[k]的插入排序
}

