栈的使用
本章我们主要介绍一下栈的使用。
1. 栈
1.1 抽象数据类型栈的定义
栈(stack)是限定仅在表尾进行插入或删除操作的线性表。因此,对栈来说,表尾端有其特殊含义,称为栈顶(top),相反地,表头端称为栈底(bottom)。不含元素的空表称为空栈。
假设栈S=(a1, a2, a3, …, an),则称a1为栈底元素,an为栈顶元素。栈中元素按a1, a2, …, an的次序进栈,退栈的第一个元素为栈顶元素。换句话说,栈的修改是按后进先出的原则进行的(如下图3.1(a)所示)。因此,栈又称为后进先出(last in first out)的线性表(简称LIFO结构),它的这个特点可用3.1(b)所示的铁路调度站形象地表示。
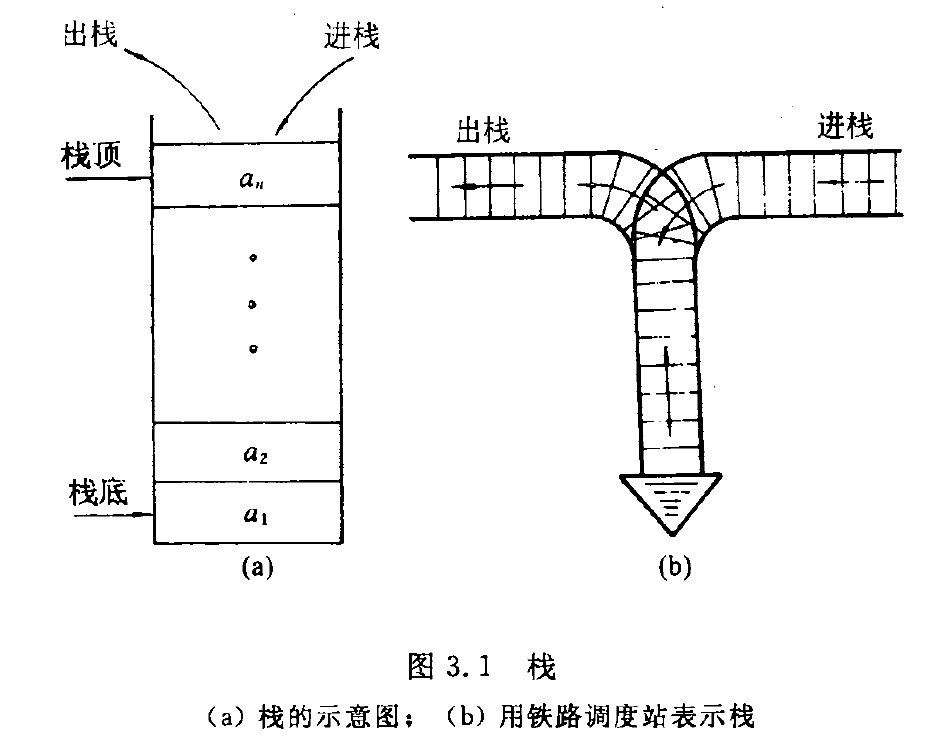
栈的基本操作除了在栈顶进行插入或删除外,还有栈的初始化、判空及取栈顶元素等。下面给出栈的抽象数据类型的定义:

1.2 栈的表示和实现
和线性表类似,栈也有两种存储表示方法。
顺序栈,即栈的顺序存储结构是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针top指示栈顶元素在顺序栈中的位置。通常的习惯做法是以top=0表示空栈,鉴于C语言中数组的下标约定从0开始,则当以C作为描述语言时,如此设定会带来很大的不便;另一方面,由于栈在使用过程中所需最大空间的大小很难估计,因此,一般来说,在初始化设空栈时不应限定栈的最大容量。一个较合理的做法是: 先为栈分配一个基本容量,然后在应用过程中,当栈的空间不够使用时再逐段扩大。为此,可设定两个常量:STACK_INIT_SIZE(存储空间初始分配量)和STACKINCREMENT(存储空间分配增量),并以下述类型说明作为顺序栈的定义。
typedef struct{
SElemType *base;
SElemType *top;
int stacksize;
}SqStack;其中,stacksize指示栈的当前可使用的最大容量。栈的初始化操作为: 按设定的初始分配量进行第一次存储分配,base可称为栈底指针,在顺序栈中,它始终指向栈底的位置,若base的值为NULL,则表明栈结构不存在。称top为栈顶指针,其初值指向栈底,即top == base可作为栈空的标记,每当插入新的栈顶元素时,指针top增1;删除栈顶元素时,指针top减1,因此,非空栈中的栈顶指针始终在栈顶元素的下一个位置上。如下图3.2展示了顺序栈中数据元素和栈顶指针之间的对应关系。
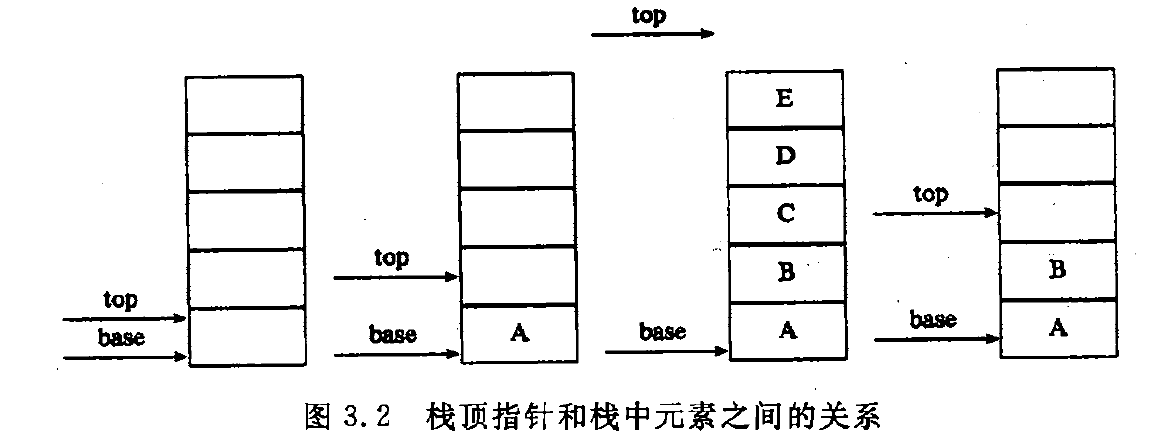
以下是顺序栈的模块说明:
//====== ADT Stack的表示与实现 ======
//----- 栈的顺序存储表示-------------
#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量
typedef struct{
SElemType *base; //在构造之前和销毁之后,base的值为NULL
SElemType *top; //栈顶指针
int stacksize; //当前已分配的存储空间,以元素为单位
}SqStack;
//-------- 基本操作的函数原型说明 -----------------
//构造一个空栈S
Status InitStack(SqStack &S);
//销毁栈S, S不再存在
Status DestroyStack(SqStack &S);
//把S置为空栈
Status ClearStack(SqStack &S);
//若S为空栈,则返回TRUE,否则返回FALSE
Status StackEmpty(SqStack S);
//返回S的元素个数,即栈的长度
int StackLength(SqStack S);
//若栈不空,则用e返回S的栈顶元素,并返回OK; 否则返回ERROR
Status GetTop(SqStack S, SElemType &e);
//插入元素e为新的栈顶元素
Status Push(SqStack &S, SElemType e);
//若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR
Status Pop(SqStack &S, SElemType &e);
//从栈底到栈顶依次对栈中每个元素调用函数visit(),一旦visit()失败,操作失败
Status StackTraverse(SqStack S, Status (*visit)());
//------ 基本操作的算法描述(部分)-------------
Status InitStack(SqStack &S)
{
//构造一个空栈
S.base = (SElemType *)malloc(STACK_INIT_SIZE *sizeof(SElemType));
if(!S.base)
exit(OVERFLOW); //存储分配失败
S.top = S.base;
S.stacksize = STACK_INIT_SIZE;
return OK;
}
Status GetTop(SqStack S, SElemType &e)
{
//若栈不空,则用e返回S的栈顶元素,并返回OK; 否则返回ERROR
if (S.top == S.base)
return ERROR;
e = *(S.top - 1);
return OK;
}
Status Push(SqStack &S, SElemType e)
{
//插入元素e为新的栈顶元素
if(S.top - S.base >= S.stacksize){ //栈满,追加存储空间
S.base = (SElemType *)realloc(S.base, (S.stacksize + STACKINCREMENT) * sizeof(SElemType));
if (!S.base)
exit(OVERFLOW); //存储分配失败
S.top = S.base + S.stacksize;
S.stacksize = S.stacksize + STACKINCREMENT;
}
*S.top++ = e;
return OK;
}
Status Pop(SqStack &S, SElemType &e)
{
//若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR
if (S.top == S.base)
return ERROR;
e = *--S.top;
return OK;
}对于栈的链式表示,如下图3.3所示。由于栈的操作是线性表操作的特例,则链栈的操作易于实现,在此不作详细讨论。
typedef struct SNode{
SElemType data;
struct SNode *prev;
struct SNode *next;
}SNode;
typedef struct{
SNode *base;
SNode *top;
int stacksize;
}LsNode, *LinkStack;
Status InitStack(LinkStack *S)
{
if(!S)
return ERROR;
*S = (LinkStack)malloc(sizeof(LsNode));
if(!*S)
exit(OVERFLOW);
(*S)->base = (*S)->top = NULL;
(*S)-stacksize = 0;
return OK;
}
Status Push(LinkStack *S, SElemType e)
{
SNode *p = (SNode *)malloc(sizeof(SNode));
if(!p)
exit(OVERFLOW);
p->prev = p->next = NULL;
p->data = e;
if((*S)->top == NULL){
(*S)->base = (*S)->top = p;
(*S)->stacksize = 1;
}else{
(*S)->top->next = p;
p->prev = (*S)->top;
(*S)->top = (*S)->top->next;
(*S)->stacksize = (*S)->stacksize+1;
}
return OK;
}
Status Pop(LinkStack *S, SElemType &e)
{
if ((*S)->base == NULL){
return ERROR;
}
if((*S)->base == (*S)->top)
{
e = (*S)->top->data;
free((*S)->top);
(*S)->top = (*S)->base = NULL;
return OK;
}
e = (*S)->top->data;
SNode *p = (*S)->top;
(*S)->top = (*S)->top->prev;
(*S)->top->next = NULL;
free(p);
return OK;
}2. 栈的应用举例
2.1 迷宫求解
求迷宫中从入口到出口的所有路径是一个经典的程序设计问题。由于计算机解迷宫时,通常用的是“穷举求解”的方法,即从入口出发,顺某一方向向前探索,若能走通,则继续往前走;否则沿原路退回,换一个方向再继续探索,直至所有可能的通路都探索到为止。为了保证在任何位置上都能沿原路退回,显然需要用一个后进先出的结构来保存从入口到当前位置的路径。因此,在求迷宫通路的算法中应用“栈”也就是自然而然的事了。
首先,在计算机中可以用如图3.4所示的方块图表示迷宫。图中的每个方块或为通道(以空白方块表示)或为墙(以带影线的方块表示)。所求路径必须是简单路径,即在求得的路径上不能重复出现同一通道块。
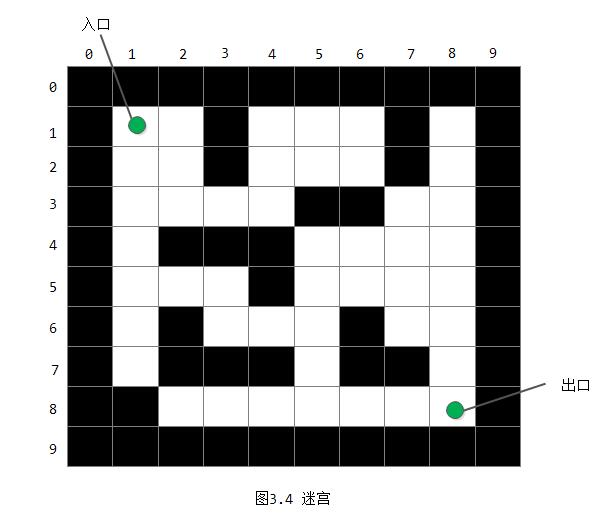
假设“当前位置”指的是“在搜索过程中某一时刻所在图中某个方块位置”,则求迷宫中一条路径的算法的基本思想是: 若当前位置“可通”,则纳入“当前路径”,并继续朝“下一位置”探索,即切换“下一位置”为“当前位置”,如此重复直至到达出口;若当前位置“不可通”,则应顺着“来向”退回到“前一通道块”,然后朝着除“来向”之外的其他方向继续探索;若该通道块的四周4个方块均“不可通”,则应从“当前路径”上删除该通道块。所谓“下一位置”指的是“当前位置”四周4个方向(东南西北)上相邻的方块。
假设以栈S记录“当前路径”,则栈顶中存放的是“当前路径上最后一个通道块”。由此,“纳入路径”的操作即为“当前位置入栈”; “从当前路径上删除前一通道块”的操作即为“出栈”。
求迷宫中一条从入口到出口的路径的算法可简单描述如下:
do{
若当前位置可通,则{
将当前位置插入栈顶; //纳入路径
若该位置是出口位置,则结束;
否则切换当前位置的东方邻块为新的当前位置;
}
否则{
若栈不空,且栈顶位置仍有其他方向未经探索,
则设定新的当前位置为沿顺时钟方向旋转找到的栈顶位置的下一邻块;
若栈不空,但栈顶位置的四周均不可通,则{
删去栈顶位置; //从路径中删去该通道块
若栈不空,则重新测试新的栈顶位置,
直至找到一个可通的相邻块或出栈至栈空;
}
}
}while(栈不空);在此,尚需说明的一点是,所谓当前位置可通,指的是未曾走到过的通道块,即要求该方块位置不仅是通道块,而且既不在当前路径上(否则所求路径就不是简单路径),也不是曾经纳入过路径的通道块(否则只能在死胡同内转圈)。
下面我们给出大体的算法实现:
Status MazePath(MazeType maze, PosType start, PosType end)
{
//若迷宫maze中存在从入口start到出口end的通道,则求得一条存放在栈中(从栈底到栈顶),
//并返回TRUE;否则返回FALSE
InitStack(S);
curpos = start; //设定"当前位置"为"入口位置"
curstep = 1; //探索第一步
do{
if(Pass(curpos)){ //当前位置可以通过,即是未曾走到过的通道块
FootPrint(curpos); //留下足迹
e = (curstep, curpos, 1);
Push(S, e); //加入路径
if(curpos == end)
return TRUE; //到达终点(出口)
curpos = NextPos(curpos, 1); //下一位置是当前位置的东邻
curstep++; //探索下一步
}
else{ //当前位置不能通过
if(!StackEmpty(S)){
Pop(S, e);
while(e.di == 4 && !StackEmpty(S)){
MarkPrint(e.seat);
Pop(S, e); //留下不能通过的标记,并退回一步
}
if(e.di < 4){
e.di++;
Push(S, e); //换下一个方向探索
curpos = NextPos(e.seat, e.di); //设定当前位置是该新方向上的相邻块
}
}
}
}while(!StackEmpty(S));
return FALSE;
}2.2 表达式求值
求值过程描述
表达式求值是程序设计语言编译中的一个最基本问题。它的实现是栈应用的又一个典型例子。这里介绍一种简单直观、广为使用的算法,通常称为算符优先法。
要把一个表达式翻译成正确求值的一个机器指令序列,或者直接对表达式求值,首先要能够正确解释表达式。例如,要对下面的算术表达式求值:
4+2x3-10/5
首先要了解算术四则运算的规则。即:
1) 先乘除,后加减
2) 从左算到右
3) 先括号内,后括号外
由此,这个算术表达式的计算顺序应为:
4+2x3-10/5 = 4+6-10/5 = 10-10/5 = 10-2 = 8
算符优先法就是根据这个运算优先关系的规定来实现对表达式的编译或解释执行的。
任何一个表达式都是由操作数(operand)、运算符(operator)和界限符(delimiter)组成的,我们称它们为单词。一般地,操作数既可以是常数也可以是被说明为变量或常量的标识符;运算符可以分为算术运算符、关系运算符和逻辑运算符3类;基本界限符有左右括号和表达式结束符等。为了叙述简洁,我们仅讨论简单算术表达式的求值问题。这种表达式只含加、减、称、除4种运算符。
我们把运算符和界限符统称为算符,它们构成的集合命名为OP。根据上述3条运算规则,在运算的每一步中,任意两个相继出现的算符θ1和θ2之间的优先关系至多是下面3种关系之一:
-
θ1<θ2: θ1的优先权低于θ2
-
θ1=θ2: θ1的优先权等于θ2
-
θ1>θ2: θ1的优先权高于θ2
下表定义了算符之间的这种优先关系:
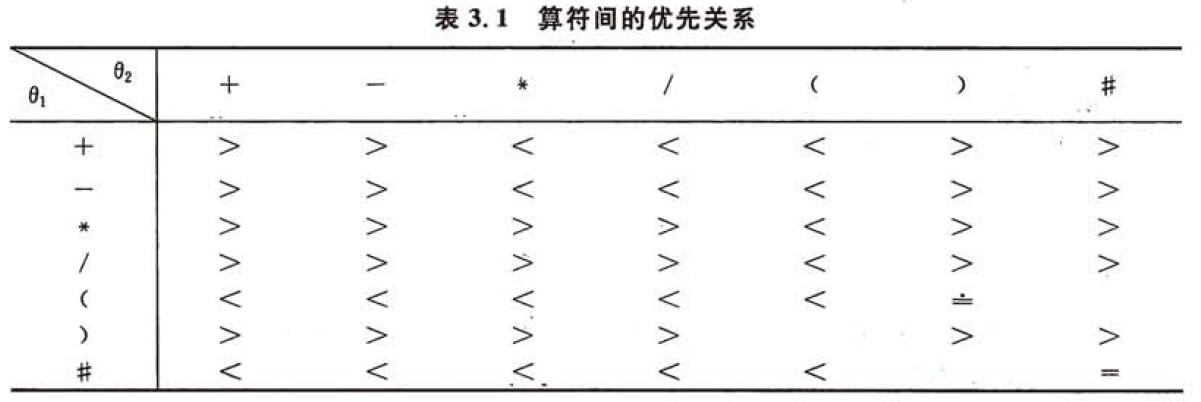
由规则3),+、-、*和/为θ1的优先性均低于(但高于); 由规则2),当θ1=θ2时,令θ1>θ2; #是表达式的结束符。为了算法简洁,在表达式最左边也虚设一个#构成整个表达式的一对括号。表中“(” = “)”表示当左右括号相遇时,括号内的运算已经完成。同理,“#” = “#”表示整个表达式求值完毕。“)”与“(”、“#”与“)” 以及 “(”与“#” 之间无优先关系,这是因为表达式中不允许它们相继出现,一旦遇到这种情况,则可以认为出现了语法错误。在下面的讨论中,我们暂假定所有输入的表达式不会出现语法错误。
为了实现算符优先算法,可以使用两个工作栈。一个称作OPTR,用于寄存运算符;另一个称作OPND,用于寄存操作数或运算结果。算法的基本思想是:
1) 首先置操作数栈为空栈,表达式起始符“#”为运算符栈的栈底元素;
2) 依次读入表达式中每个字符,若是操作数则进OPND栈,若是运算符则和OPTR的栈顶运算符比较优先权后作相应操作,直至整个表达式求值完毕(即OPTR的栈顶元素和当前读入的字符均为“#”)
算法实现
如下描述了表达式求值的过程:
//算术表达式求值的算符优先算法。设OPTR和OPND分别为运算符栈和运算数栈, OP为运算符集合
OperandType EvaluateExpression()
{
InitStack(OPTR);
Push(OPTR,'#');
InitStack(OPND);
c = getchar();
while(c != '#' || GetTop(OPTR) != '#')
{
if(!In(c, OP))
{
//不是运算符则进栈
Push(OPND,c);
c = getchar();
}
else{
switch(Precede(GetTop(OPTR),c))
{
case '<':
{
//栈顶元素优先权低
Push(OPTR,c);
c = getchar();
break;
}
case '=':
{
//脱括号,并接收下一字符
Pop(OPTR,x);
c = getchar();
break;
}
case '>':
{
//退栈并将运算结果入栈
Pop(OPTR,theta);
Pop(OPND,b);
Pop(OPND,a);
Push(OPND,Operate(a,theta,b));
break;
}
}
}
}
return GetTop(OPND);
}上面算法中还调用了两个函数。其中,Precede()函数是判定运算符栈的栈顶运算符θ1与读入的运算符θ2之间优先关系的函数; Operate()函数为进行二元运算a θ b的函数,如果是编译表达式,则产生这个运算的一组相应指令并返回存放结果的中间变量名;如果是解释执行表达式,则直接进行该运算,并返回运算的结果。
运算示例
如下是利用上述算法对算术表达式3*(7-2)求值,操作过程如下所示:
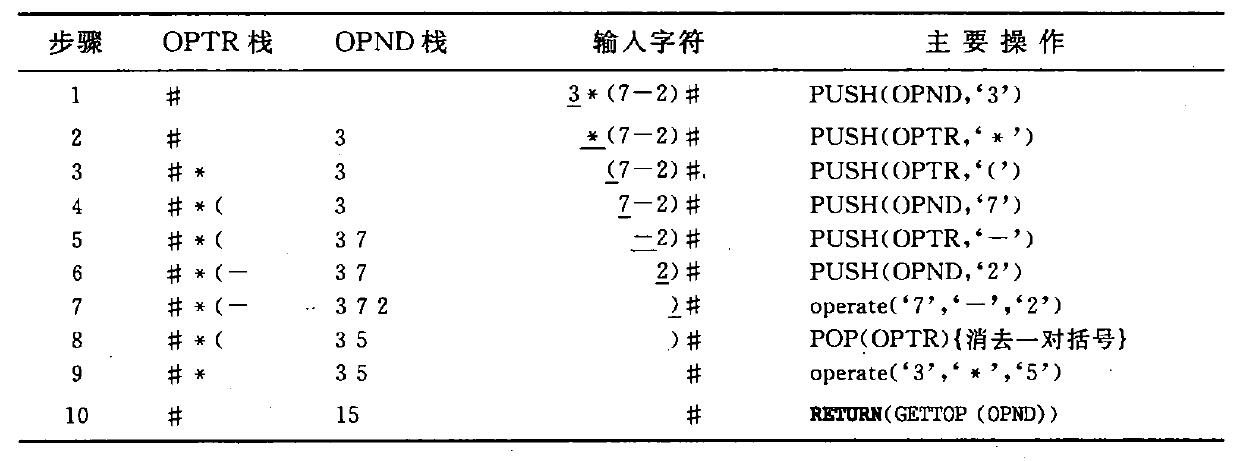
2.3 栈与递归的实现
栈还有一个重要应用是在程序设计语言中实现递归。一个直接调用自己或通过一系列的调用语句间接调用自己的函数,称作递归函数。下面我们来看一个n阶汉诺塔问题。
n阶汉诺塔问题
假设有3个分别命名为X、Y和Z的塔座,在塔座X上插有n个直径大小各不相同、依小到大编号为1、2、…、n的圆盘(如下图所示)。现要求将X轴上的n个圆盘移至塔座Z上并按同样的顺序叠排,圆盘移动时必须遵守如下规则。
1) 每次只能移动一个圆盘;
2) 圆盘可以插在X、Y和Z中的任一塔座上;
3) 任何时刻都不能将一个较大的圆盘压在较小的圆盘之上。
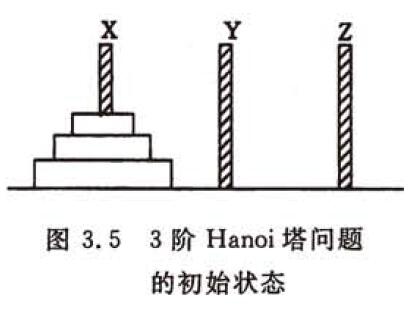
如何实现移动圆盘的操作呢? 当n=1时,问题比较简单,只要将编号为1的圆盘从塔座X直接移至塔座Z上即可;当n>1时,需利用塔座Y作辅助塔座,若能设法将压在编号为n的圆盘之上的n-1个圆盘从塔座X(依照上述法则)移至塔座Y上,则可先将编号为n的圆盘从塔座X移至塔座Z上,然后再将塔座Y上的n-1个圆盘(依照上述法则)移至塔座Z上。而如何将n-1个圆盘从一个塔座移至另一个塔座的问题是一个和原文件具有相同特征属性的问题,只是问题的规模小1,因此可以用同样的方法求解。由此我们可以用如下算法来求解n阶Hanoi塔问题:
//将塔座x上按直径由小到大且自上而下编号为1至n的n个圆盘按规则搬到塔座z上,y可用作辅助塔座
//移动操作move(x,n,z)可定义为(c是初值为0的全局变量,对搬动计数):
void move(char x, int n, char z)
{
printf("%i. Move disk %i from %c to %c\n", ++c, n, x,z);
}
void hanoi(int n,char x,char y, char z)
1 {
2 if(n == 1)
3 move(x,1,z);
4 else{
5 hanoi(n-1,x,z,y); //将x上编号为1至n-1的圆盘移到y,z作辅助塔
6 move(x,n,z); //将编号为n的圆盘从x移到z
7 hanoi(n-1,y,x,z); //将y上编号为1至n-1的圆盘移到z,x作为辅助塔
8 }
9 }函数调用栈分析
上面hanoi()函数是一个递归函数,在函数的执行函数中,需多次进行自我调用。那么,这个递归函数是如何执行的? 先看任意两个函数之间进行调用的情形。
与汇编程序设计中主程序和子程序之间的链接及信息交换类似,在高级语言编制的程序中,调用函数和被调用函数之间的链接及信息交换需通过栈来进行。
通常,当在一个函数的运行期间调用另一个函数时,在运行被调用函数之前,系统需完成3件事:1) 将所有的实际参数、返回地址等信息传递给被调用函数保存; 2) 为被调用函数的局部变量分配存储区; 3) 将控制转移到被调函数的入口。 而从被调函数返回调用函数之前,系统也应完成3件工作: 1) 保存被调函数的计算结果; 2) 释放被调函数的数据区; 3) 依照被调函数保存的返回地址将控制转移到调用函数。当有多个函数构成嵌套调用时,按照“后调用先返回”的原则,上述函数之间的信息传递和控制转移必须通过“栈”来实现,即系统将整个程序运行时所需的数据空间安排在一个栈中,每当调用一个函数时,就为它在栈顶分配一个存储区,每当从一个函数退出时,就释放它的存储区,则当前正运行的函数的数据区必在栈顶。如下图(c)所示主函数main中调用了函数first(),而在函数first()中又调用了函数second(),则下图(a)展示了当前正在执行函数second()中某个语句时栈的状态,而图(b)展示从函数second()退出之后正执行函数first()中某个语句时栈的状态(图中以语句标号表示返回地址):
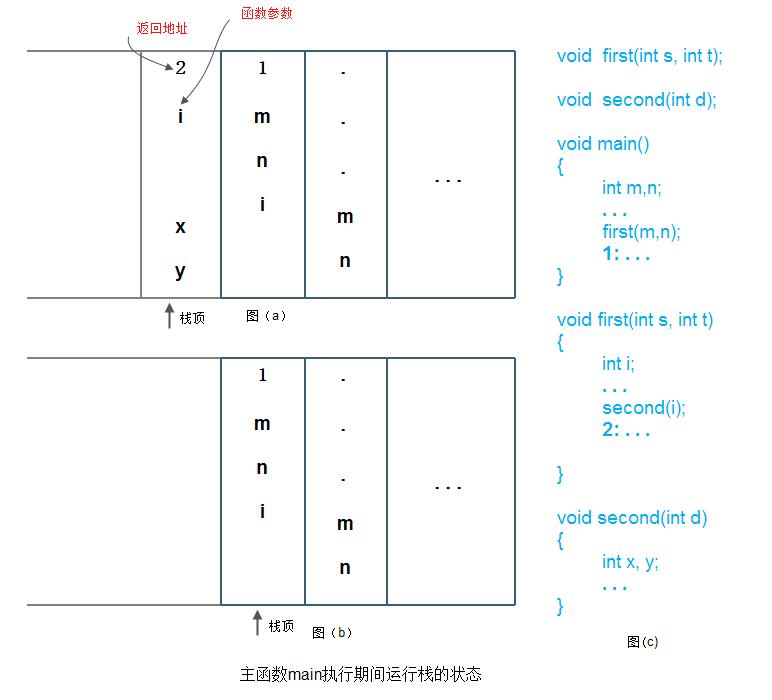
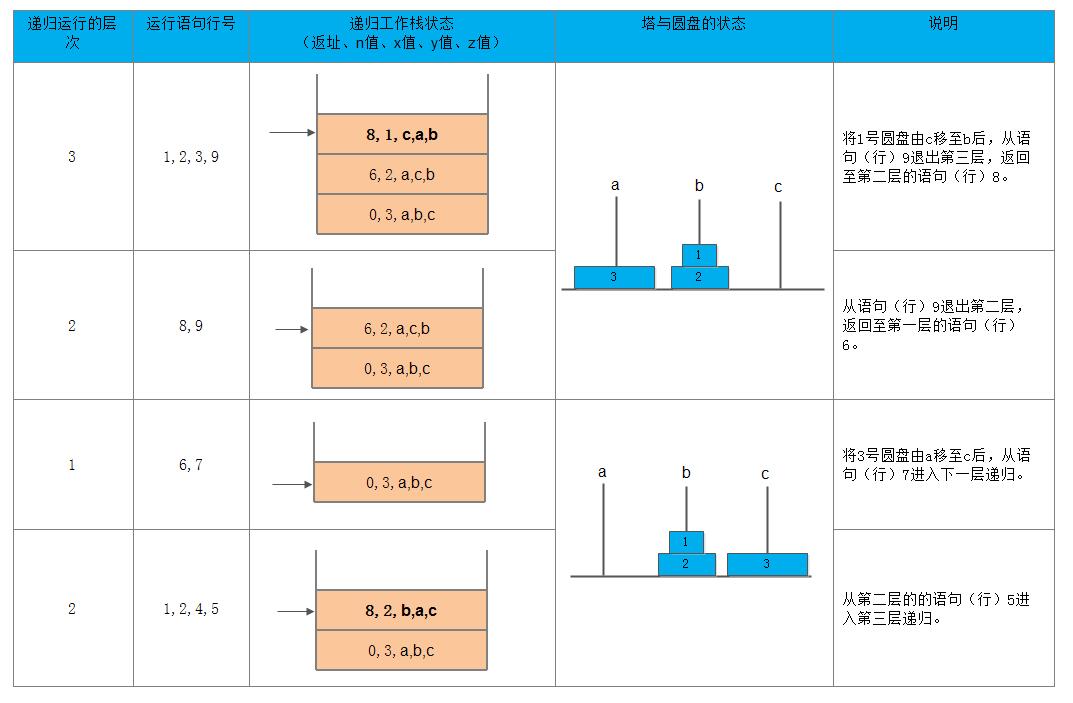
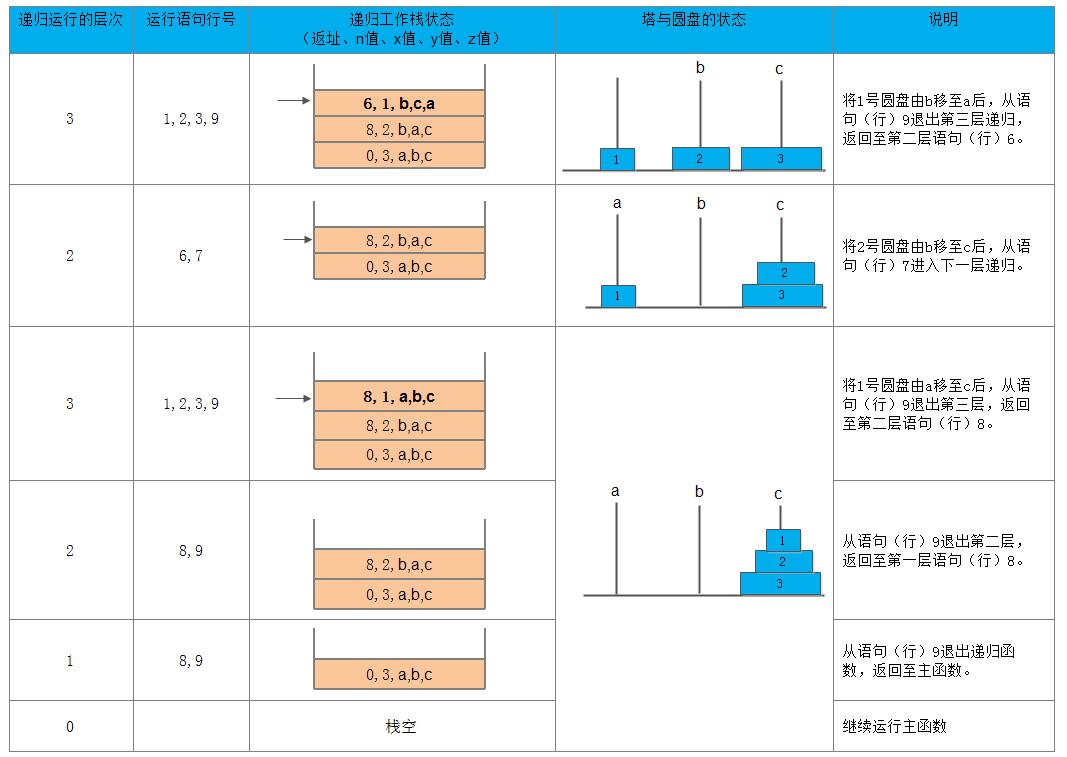
一个递归函数的运行过程类似于多个函数的嵌套调用,只是调用函数和被调用函数是同一个函数,因此,和每次调用相关的一个重要概念是递归函数运行的层次。假设调用该递归函数的主函数为第0层,则从主函数调用递归函数进入第1层;从第i层递归调用本函数为进入“下一层”,即第i+1层。反之,退出第i层递归应返回至上一层,即第i-1层。为了保证递归函数正确执行,系统需设立一个递归工作栈作为整个递归函数运行期间使用的数据存储区。每一层递归所需信息构成一个“工作记录”,其中包括所有实际参数、所有的局部变量以及上一层的返回地址。每进入一层递归,就产生一个新的工作记录压入栈顶。每退出一层递归,就从栈顶弹出一个工作记录,则当前执行层的工作记录必是递归工作栈栈顶的工作记录,称这个记录为“活动记录”,并称指示活动记录的栈顶指针为“当前环境指针”。
例如,下图展示了语句:
hanoi(3,a,b,c);
执行过程(从主函数进入递归函数到退出递归函数而返回主函数)中递归工作栈状态的变化情况。由于上面算法所示的递归函数中只含有4个值参数,则每个工作记录包含5个数据项: 返回地址和4个实际参数,并以递归函数中的语句行号表示返回地址,同时假设主函数的返回地址为0。图中以箭头指示栈顶指针。
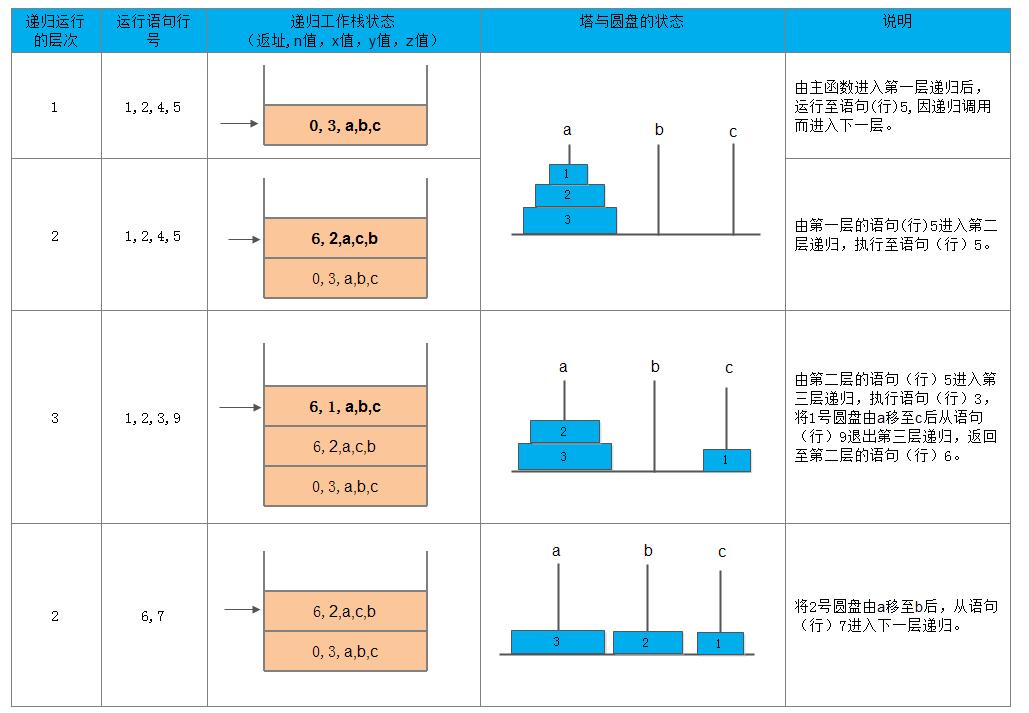
实际上,在调用函数和被调用函数之间不一定传递参数的值,也可以传递参数的地址。通常,每个程序设计语言都有它自己约定的传递方法(包括被调用函数的执行结果如何返回调用函数等)。
由于递归函数结构清晰,程序易读,而且它的正确性容易得到证明,因此,利用允许递归调用的语言(例如C语言)进行程序设计时,给用户编制程序和调试程序带来很大方便。因为对这样一类递归问题编程时,不需用户自己而由系统来管理递归工作栈。

