串的模式匹配算法
本章我们主要介绍一下串的模式匹配算法。
1. 求子串位置的定位函数
子串的定位操作通常称作串的模式匹配(其中T称为模式串),是各种串处理系统中最重要的操作之一。下面我们给出一个采用定长顺序存储结构的子串定位算法:
#define MAXSTRLEN 255 //用户可在255以内定义最大串长
typedef unsigned char SString[MAXSTRLEN+1]; //0号单元存放串的长度
//返回子串T在主串S中第pos个字符起的位置。若不存在,则函数值为0
//其中,T非空, 1<=pos<=StrLen(S)
int Index(SString S, SString T, int pos)
{
i=pos;
j = 1;
while(i <= S[0] && j <= T[0])
{
if(S[i] == T[j]
{
++i;
++j;
}
else{
i = i - j + 2; //指针后退重新开始匹配
j = 1;
}
}
if(j > T[0])
return i-T[0];
else
return 0;
}在上面算法中,分别利用计数指针i和j指示主串S和模式串T中当前正待比较的字符位置。算法的基本思想是: 从主串S的第pos个字符起和模式的第一个字符比较之,若相等,则继续逐个比较后续字符; 否则从主串的下一个字符起再重新和模式的字符比较之。依次类推,直至模式T中的每个字符依次和主串S中的一个连续的字符序列相等,则称匹配成功,函数值为和模式T中第一个字符相等的字符在主串S中的序号;否则称匹配不成功,函数值为0。下图展示了模式T=’abcac’和主串S的匹配过程(pos=1)。
第一趟匹配:
↓i=3
a b a b c a b c a c b a b
a b c
↑j=3
第二趟匹配:
↓i=2
a b a b c a b c a c b a b
a
↑j=1
第三趟匹配:
↓i=7
a b a b c a b c a c b a b
a b c a c
↑j=5
第四趟匹配:
↓i=4
a b a b c a b c a c b a b
a
↑j=1
第五趟匹配:
↓i=5
a b a b c a b c a c b a b
a
↑j=1
第六趟匹配:
↓i=11
a b a b c a b c a c b a b
a b c a c
↑j=6上述算法的匹配过程易于理解,且在某些应用场合,如文本编辑等,效率也较高,例如,在检查模式’STING’是否存在于下列主串中时:
‘A STRING SEARCHING EXAMPLE CONSISTING of SIMPLE TEXT’
上述算法中while循环次数(即进行单个字符比较的次数)为41,恰好为(Index + T[0]-1)+4, 这就是说,除了主串中呈黑色体的4个字符,每个字符比较了两次以外,其他字符均只和模式进行一次比较。在这种情况下,此算法的时间复杂度为O(n+m)。其中,n和m分别为主串和模式的长度。然而,在有些情况下,该算法的效率却很低。例如,当模式串为’00000001’,而主串为’00000000000000000000000000000000000000000000000000001’时,由于模式中前7个字符均为’0’,主串中前52个字符均为0,每趟比较都在模式的最后一个字符出现不等,此时需将指针i回溯到i-6的位置上,并从模式的第一个字符开始重新比较,这个匹配过程中指针i需回溯45次,则while循环次数为46 * 8(index * m)。可见,上述算法在最坏情况下的时间复杂度为O(n*m)。这种情况在只有0、 1两种字符的文本串处理中经常出现,因为在主串中可能存在多个和模式串“部分匹配”的子串,因而引起指针i的多次回溯。01串可以用在许多应用之中。比如一些计算机的图形显示就是把画面表示为一个01串,一页书就是一个几百万个0和1组成的串。在二进位计算机上实际处理的都是01串。一个字符的ASCII码也可以看成是8个二进位01串。包括汉字存储在计算机中处理时也是作为一个01串和其他的字符串一样看待。因此下面我们会介绍另一种较好的模式匹配算法。
2. 模式匹配的一种改进算法
这种改进算法是D.E.Knuth与V.R.Pratt和J.H.Morris同时发现的,因此人们称它为克努特-莫里斯-普拉特操作(简称KMP算法)。此算法可以在O(n+m)的时间数量级上完成串的模式匹配操作。其改进在于: 每当一趟匹配过程中出现字符比较不等时,不需要回溯i指针,而是利用已经得到的部分匹配的结果将模式向右“滑动”尽可能远的一段距离后,继续进行比较。下面我们先从具体的例子看起。
回顾我们上一节的匹配过程示例,在第三趟的匹配中,当i=7、j=5字符比较不等时,又从i=4、j=1重新开始比较。然后,经仔细观察可发现,在i=4和j=1, i=5和j=1以及i=6和j=1这3次比较都是不必进行的。因为从第三趟部分匹配的结果就可得出,主串中第4、5和6个字符必然是’b’、’c’和’a’(即模式串中第2、3和4个字符)。因为模式中的第一个字符是a,因此它无需再和这3个字符进行比较,而仅需将模式向右滑动3个字符的位置继续进行i=7、j=2时的字符比较即可。同理,在第一趟匹配中出现字符不等时,仅需将模式向右移动两个字符的位置继续进行i=3,j=1时的字符比较。由此,在整个匹配过程中,i指针没有回溯。如下图所示为改进算法的匹配过程示例:
第一趟匹配:
↓i=3
a b a b c a b c a c b a b
a b c
↑j=3
第二趟匹配:
↓i ---> ↓i=7
a b a b c a b c a c b a b
a b c a c
↑ ----> ↑
j=1 j=5
第三趟匹配:
↓i ---> ↓i=11
a b a b c a b c a c b a b
(a)b c a c
↑ ----> ↑
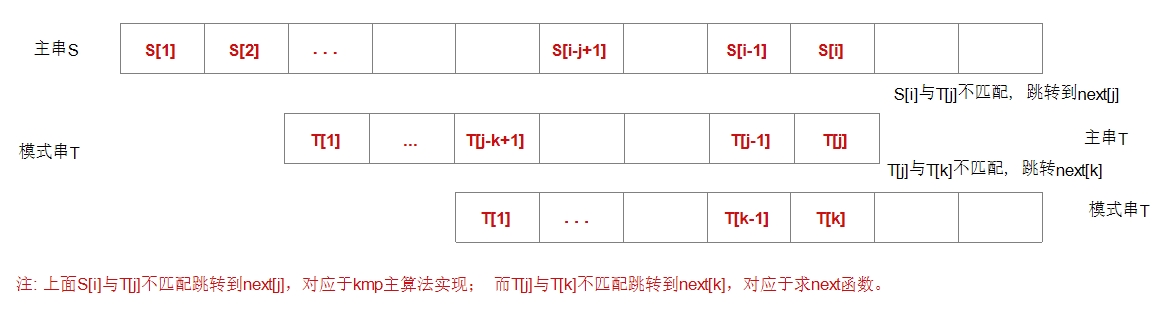
j=2 j=6现在讨论一般情况。假设主串为’S1S2…Sn’, 模式串为’P1P2…Pm’, 从上面分析可知,为了实现改进算法,需要解决下述问题: 当匹配过程中产生“失配”(及Si != Pj)时,模式串“向右滑动”可行的距离多远,换句话说,当主串中第i个字符与模式中第j个字符“失配”(即比较不等)时,主串中第i个字符(i指针不回溯)应与模式中哪个字符再比较?
假设此时应与模式中第k(k<j)个字符继续比较,则模式中前k-1个字符的子串必须满足如下关系式(4-2),且不可能存在k’>k满足如下关系式(4-2):
'P1P2...Pk-1' = 'Si-k+1Si-k+2...Si-1' (4-2)而已经得到的部分匹配的结果是:
'Pj-k+1Pj-k+2...Pj-1' = 'Si-k+1Si-k+2...Si-1' (4-3)由上式(4-2)和式(4-3)推得下列等式:
'P1P2...Pk-1' = 'Pj-k+1Pj-k+2...Pj-1' (4-4)反之,若模式串中存才满足式(4-4)的两个子串,则当匹配过程中,主串中第i个字符与模式中第j个字符比较不相等时,仅需将模式向右滑动至模式中第k个字符和主串中第i个字符对齐,此时,模式中头k-1个字符的子串'P1P2...Pk-1'必定与主串中第i个字符之前长度为k-1的子串'Si-k+1Si-k+2...Si-1'相等,由此,匹配仅需从模式中第k个字符与主串中第i个字符比较起继续进行。
若令next[j]=k,则next[j]表明当模式中第j个字符与主串中相应字符“失配”时,在模式中需重新和主串中该字符进行比较的字符的位置。由此,可引出模式串的next函数的定义:
 由此定义可推出下列模式串的next函数值:
由此定义可推出下列模式串的next函数值:
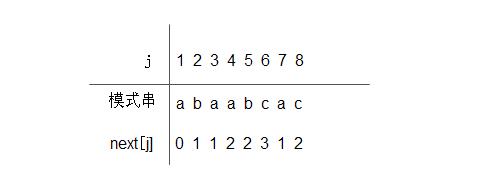
在求得模式的next函数之后,匹配可如下进行: 假设以指针i和j分别指示主串和模式中正待比较的字符,令i的初值为pos,j的初值为1。若在匹配过程中si=pj,则i和j分别增1;否则,i不变,而j退到next[j]的位置再比较,若相等,则指针各自增1,否则j再退到下一个next值的位置,依次类推,直至下列两种可能:
-
1) j退到某个next值(next[next[…next[j]..]])时字符比较相等,则指针各自增1,继续进行匹配;
-
2) j退到值为0(即模式的第一个字符失配),此时需将模式继续向右滑动一个位置,即从主串的下一个字符
Si+1起和模式重新开始匹配。
如下图是上述匹配过程的一个例子(模式为’abaabcac’):
↓i=2
主串 a c a b a a b a a b c a c a a b c
第一趟匹配
模式 a b
↑j=2 next[2]=1
↓i=2
主串 a c a b a a b a a b c a c a a b c
第二趟匹配
模式 a b
↑j=1 next[1] = 0
↓i=3 ---> ↓i=8
主串 a c a b a a b a a b c a c a a b c
第三趟匹配
模式 a b a a b c
↑j=1 ---->↑j=6 next[6] = 3
↓i=8 -----> ↓i=14
主串 a c a b a a b a a b c a c a a b c
第四趟匹配
模式 (a b)a a b c a c
↑j=3 ------>↑j=9 2.1 KMP算法
KMP算法如下所示,它在形式上与开头介绍的直接定位函数类似。不同之处仅在于:当匹配过程中产生失配时,指针i不变,指针j退回到next[j]所指示的位置上重新进行比较,并且当指针j退至零时,指针i和指针j需同时增1.即若主串的第i个字符和模式的第1个字符不等,应从主串的第i+1个字符起重新进行匹配。
//利用模式串T的next函数求T在主串S中第pos个字符之后的位置的
//KMP算法。其中,T非空,1<=pos<=StrLength(S)
int Index_KMP(SString S, SString T, int pos)
{
i = pos;
j = 1;
while(i <= S[0] && j <= T[0])
{
if(j == 0 || s[i] == s[j])
{
++i;
++j;
}
else{
j = next[j];
}
}
if(j > T[0])
return i-T[0];
else
return 0;
}2.2 求next函数
KMP算法是在已知模式串的next函数值的基础上执行的,那么,如何求得模式串的next函数值呢? 从上述讨论可见,此函数值仅取决于模式串本身而和相匹配的主串无关。我们可从分析其定义出发用递推的方法求得next函数值。
由定义得知,
next[1] = 0 (4-6)
设next[j] = k,这表明在模式串中存在下列关系:
'P1P2..Pk-1' = 'Pj-k+1Pj-k+2...Pj-1' (4-7)
其中k为满足1<k<j的某个值,并且不可能存在k'>k满足等式(4-7)。此时next[j+1]=?可能有两种情况:
1) 情形1: Pk=Pj
若Pk=Pj,则表明在模式串中
'P1P2...Pk = 'Pj-k+1Pj-k+2...Pj' (4-8)
并且不可能存在k'>k满足上式,这也就是说next[j+1] = k+1,即:
next[j+1] = next[j] + 1 (4-9)
2) 情形2: Pk!=Pj
若Pk!=Pj,则表明在模式串中
'P1P2...Pk' != 'Pj-k+1Pj-k+2...Pj'
此时可把求next函数值的问题看成是一个模式匹配的问题。整个模式串既是主串又是模式串,而当前在匹配的过程中,已有P1=Pj-k+1, P2=Pj-k+2,…, Pk-1=Pj-1,则当Pj!=Pk时应将模式向右滑动至以模式中的第next[k]个字符和主串中的第j个字符相比较。若next[k]=k',且Pj=Pk',则说明在主串中第j+1个字符之前存在一个长度为k'(即next[k])的最长子串,和模式串中从首字母起长度为k'的子串相等,即:
'P1P2..Pk'' = 'Pj-k'+1Pj-k'+2...Pj' (1<k'<k<j) (4-10)也就是说next[j+1] = k’+1,即:
next[j+1] = next[k] + 1 (4-11)
同理,若Pj!=Pk',则将模式继续向右滑动直至将模式中第next[k’]个字符和Pj对齐, …, 依次类推,直至Pj和模式中某个字符匹配成功或者不存在任何k'(1<k’<j)满足等式(4-10),则:
next[j] = 1 (4-12)
例如,下图所示的模式串,以求得前6个字符的next函数值,现求next[7],因为next[6]=3,又P6!=P3,则需比较P6和P1(因为next[3]=1),这相当于将子串模式向右滑动。由于P6 != P1,而且next[1] = 0,所以next[7]=1,而因P7=P1,则next[8]=2。

下面根据上述分析所得结果(式(4-6)、(4-9)、(4-11)和(4-12)),仿照KMP算法,可得到求next函数值的算法:
//求模式串T的next函数值并存入数组next
void get_next(SString T, int next[])
{
i = 1;
next[1] = 0;
j = 0;
while(i < T[0])
{
if(j == 0 || T[i] == T[j])
{
++i;
++j;
next[i] = j;
}
else{
j = next[j];
}
}
}2.3 kmp算法时间复杂度
上面求next的算法时间复杂度为O(m)。通常,模式串的长度m比主串的长度n要小的多,因此,对整个匹配算法来说,所增加的这点时间是值得的。最后要说明两点:
1) 虽然串的直接模式匹配算法Index()的时间复杂度是O(n*m),但在一般情况下,其实际的执行时间近似于O(n+m),因此至今仍被采用。KMP算法仅当模式与主串之间存在"部分匹配"的情况下才显得比直接模式匹配Index()快得多。但是KMP算法的最大特点是指示主串的指针不需要回溯,整个匹配过程中,对主串仅需从头至尾扫描一遍,这对处理从外设输入的庞大文件很有效,可以边读入边匹配,而无需回头重读。
2)前面定义的next函数在某些情况下尚由缺陷。例如模式'aaaab'在和主串'aaabaaaab'匹配时,当i=4、j=4时,S.ch[4] != T.ch[4],由next[j]的指示还需进行i=4、j=3, i=4、j=2和i=4、j=1这三次比较。

实际上,因为模式中第1、2、3个字符和第4个字符都相等,因此不需要再和主串中第4个字符相比较,而可以将模式一气向右滑动4个字符的位置直接进行i=5、j=1时的字符比较。这就是说,若按上述定义得到next[j]=k,而模式中Pj=Pk,则当主串中字符Si和Pj比较不相等时,不需要再和Pk进行比较,而直接和Pnext[k]进行比较,换句话说,此时的next[j]应和next[k]相同。由此可得计算next函数修正值的算法如下。此时匹配算法不变:
//求模式串T的next函数修正值并存入数组nextval
void get_nextval(SString T, int nextval[])
{
i = 1;
nextval[1] = 0;
j = 0;
while(i < T[0])
{
if(j == 0 || T[i] == T[j])
{
++i;
++j;
if(T[i] != T[j])
nextval[i] = j;
else
nextval[i] = nextval[j];
}
else{
j = nextval[j];
}
}
}参看如下图示:

[参考]

