跳跃表的实现

本章我们主要介绍以下跳跃表的实现。

1. Skip List介绍

skip list在wiki中介绍如下：在计算机科学中，skip list是一种允许对有序序列进行快速查找的数据结构。通过维持一个链式层级结构，每一个后继序列都会跳过比上层更少的元素，这样就使得快速查找成为可能，请参看下图。查找一般会从最顶层的稀疏序列开始，直到找到两个元素，其中一个小于等于所查找元素，另一个大于等于所查找元素。

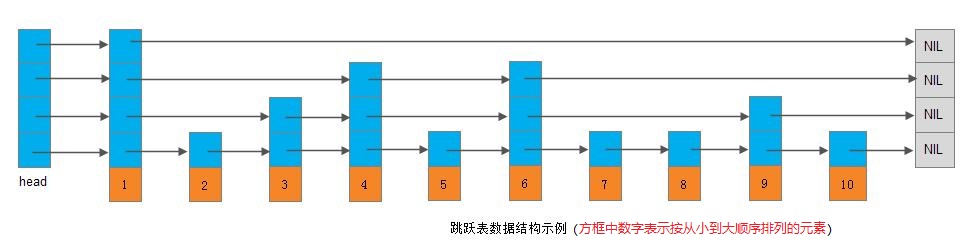
ds-skip-list

skip list是一种随机化的数据结构，其效率可比拟于二叉查找树（对于大多数操作需要O(logn)平均时间）。跳跃表是在很多应用中有可能替代平衡树而作为实现方法的一种数据结构。跳跃表的算法有同平衡树一样的渐进的预期时间边界，并且更简单、更快速和使用更少的空间。目前开源的Redis和LevelDB都有用到它，它的效率和红黑树以及AVL树不相上下，但是跳跃表的原理相当简单，只要能熟练操作链表，就能轻松实现一个Skip List。跳跃表是有Pugh在1990年提出的。

2. skip list定义及构造步骤

2.1 跳跃表的性质

首先应该了解跳跃表的性质：

一个跳跃表应该由多个层(level)组成；
每一层都是一个有序的链表，排列顺序为由高层到底层，都至少包含两个链表节点，分别是前面的head节点和后面的nil节点；
最底层（level 1)的链表包含了所有元素；
如果一个元素出现在某一层的链表中，那么在该层之下的链表也全都会出现;
每个节点包含两个指针，一个指向同一层链表中的下一个元素，另一个指向下面一层具有相同值的元素；

参照上面所示的跳跃表，可以看到总共有4层，最上面一层是最高层（Level4)，最下面一层是最底层（level1)，然后每一列中的链表节点的值都相同，用指针来链接着。跳跃表的层数跟结构中最高节点的高度相同。理想情况下，跳跃表结构中第一层存在所有节点，第二层只有一半的节点，而且是均匀间隔的，第三层则存在1/4的节点，并且是均匀间隔的，以此类推，这样理想的层数就是logN。

2.2 跳跃表数据结构

typedef struct skiplist_node{
	double score;
	void *obj;
	struct skiplist_node *backward;

	int levels;
	struct skiplist_node_level{
		struct skiplist_node *forward;
		//unsigned int span;
	}level[];
}skiplist_node;

typedef struct skiplist{
	struct skiplist_node *header;
	struct skiplist_node *tail;

	int level;
	int length;

	void (*free)(void *obj);
	int (*match)(void *obj1, void *obj2);
};

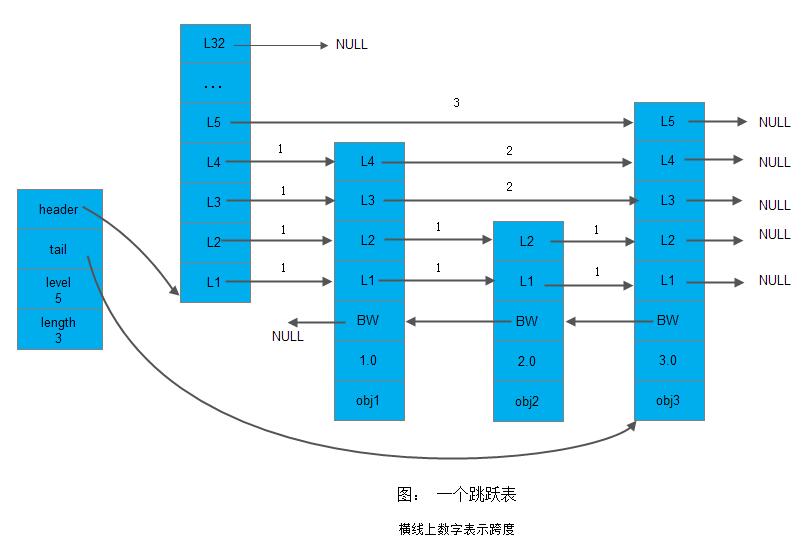
下面先给出跳跃表数据结构的一个示意图：

ds-skip-list

下面我们分别讲述一下上面两个数据结构各字段含义：

1) struct skiplist数据结构

skiplist是表示跳跃表的数据结构，其各属性字段含义如下：

header: 指向跳跃表的表头节点；
tail: 指向跳跃表的表尾节点；
level: 记录目前跳跃表内，层数最大的那个节点的层数（表头节点的层数不计算在内）。
length: 记录跳跃表的长度，也即是，跳跃表目前包含节点的数量（表头节点不计算在内)。
free: 用于释放obj对象的回调函数
match: 用于比较两个obj对象的函数

在skiplist结构中，obj按score有序。

2) struct skiplist_node数据结构

skiplist_node代表跳跃表的一个节点，其各属性的含义如下：

levels: 用于保存节点的层数。比如上边score为1.0的节点，层数为4； score为2.0的节点，层数为2； score为3.0的节点，层数为5.
level: 代表着各层，节点中L1、L2、L3等字样标记节点的各个层。L1代表第一层， L2代表第二层，以此类推。每个层有一个前进指针和跨度(注：上面数据结构中我们注释了span,暂未使用）。前进指针用于访问位于表尾方向的其他节点，而跨度则记录了前进指针所指向节点和当前节点的距离。在上面图中，连线上带有数字的箭头就代表前进指针，而那个数字就是跨度。当程序从表头向表尾进行遍历时，访问会沿着层的前进指针进行。注意这里level定义的是一个零长度数组，因此需要放在结构体的最后。实际上，我们可以定义为level[1]，因为对于一个节点至少有一个前进指针，这样我们就可以把该字段存放在任何位置了。
backward指针：节点中用BW字样标记节点的后退指针，它指向位于当前节点的前一个节点。后退指针在程序从表尾向表头遍历时使用。
score: 各个节点中的1.0、2.0和3.0是节点所保存的分值。在跳跃表中，节点按各自所保存的分值从小到大排列。
obj: 各个节点中的obj1、obj2和obj3是节点所保存的成员对象。

注意表头节点和其他节点的构造是一样的：表头节点也有后退指针、分值和成员对象，不过表头节点的这些属性都不会被用到，所以上图省略了这些部分，只显示了表头节点的各个层。

2.3 跳跃表的初始化

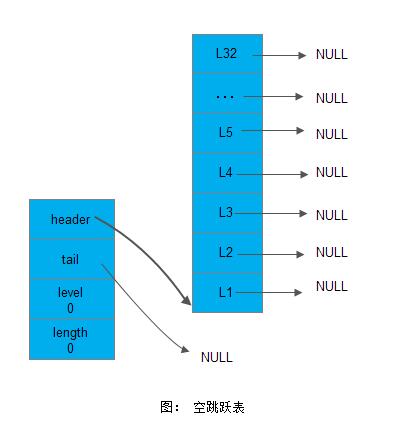
如下图所示是一个初始化的空跳跃表：

ds-skip-list-empty

下面给出相应的代码实现：

// create skiplist node
skiplist_node *create_skiplist_node(int levels, double score, void *obj)
{
	skiplist_node *node = (skiplist_node *)malloc(sizeof(skiplist_node) + levels * sizeof(struct skiplist_node_level));
	if(!node)
		return NULL;

	node->levels = levels;
	node->score = score;
	node->obj = obj;
	node->backward = NULL;

	while(levels)
	{
		node->level[--levels].forward = NULL;
	}

	return node;

}

//Init skiplist
skiplist *skiplist_create()
{
	skiplist *sl = (skiplist *)malloc(sizeof(skiplist));
	if(!sl)
		return NULL;
	sl->header = create_skiplist_node(SKIPLIST_MAX_LEVEL,0.0,NULL);
	if(!sl->header)
	{
		free(sl);
		return NULL;
	}

	sl->tail = NULL;
	sl->level = 0x0;
	sl->length = 0x0;
	sl->free = NULL;
	sl->match = NULL;

	srandom(time(0));   //for later used
	return sl;
}

2.4 跳跃表的搜索

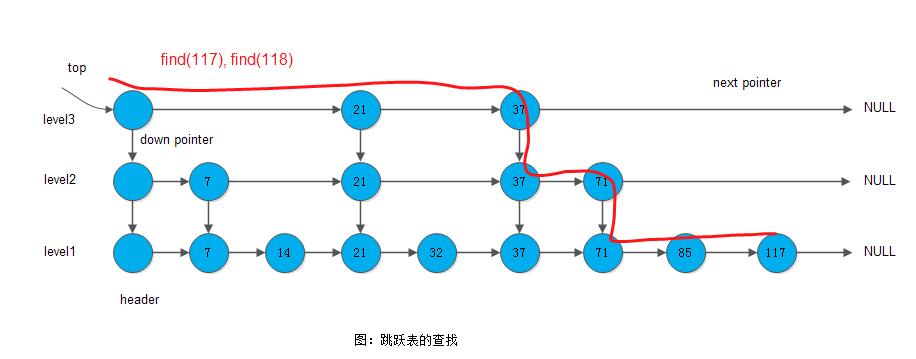
在跳跃表中查找一个元素x，按照如下几个步骤进行：

1) 从最上层的链的开头开始；

2)  假设当前位置为p，它向右指向的节点为q，且q的值为y，将 y 与 x 作比较：
    2.1) x == y，输出查询成功及相关信息；
    2.2) x > y, 从p向右移动到q的位置；
    2.3) x < y, 从p向下移动一格；

3) 如果当前位置在最底层的链中，且还要往下移动的话，则输出查询失败；

参看下图所示：

ds-skip-list-search

下面我们给出跳跃表搜索的代码(注：当score相等时，如下搜索代码其实存在一些问题)：

//这里我们参照相关代码，添加了一个内部使用的队列（实际上，我们不需要这样一个队列)
//For internal use
typedef struct s_queue{
	int matches;
	int slots;
	void **objs;
}s_queue;

s_queue *s_queue_init()
{
	int slots = 4;
	s_queue *queue = (s_queue *)malloc(sizeof(s_queue));
	if(!queue)
		return NULL;
	queue->objs = (void **)malloc(sizeof(void *)*slots);
	if(!queue->objs)
	{
		free(queue);
		return NULL;
	}
	queue->slots = slots;
	queue->matches = 0x0;
	return queue;
}

int s_queue_push(s_queue *queue, void *obj)
{
	if(queue->matches >= queue->slots)
	{
		int slots = queue->slots >> 1;
		void **objs = (void **)realloc(queue->objs, slots * sizeof(void *));
		if(!objs)
			return -1;

		queue->objs = objs;
		queue->slots = slots;
	}

	queue->objs[queue->matches++] = obj;
	return 0x0;

}

static skiplist_node **skiplist_search_all(skiplist *sl, double score, int *count)
{
	int i;
	skiplist_node *p = sl->header;
	skiplist_node **result = NULL;
	s_queue *queue = s_queue_init();
	if(!queue)
		return NULL;

	for(i = sl->level-1; i >= 0; i--)
	{
		while(p->level[i].forward && (p->level[i].forward->score <= score))
		{
			if(p->level[i].forward->score == score)
			{
				s_queue_push(queue, p->level[i].forward);
			}
			p = p->level[i].forward;
		}
	}

	if(*count = queue->matches)
	{
		result = queue->objs;
	}
	else{
		//have no matched object, 
		free(queue->objs);		
	}
	free(queue);
	
	return result;
}


void skiplist_search(skiplist *sl, double score, int *count, void *filter, void ***search_result)
{
	int matches = 0x0;
	int i;
	s_queue *queue = s_queue_init();
	if(!queue)
	{
		*count = 0;
		*search_result = NULL;
		return;
	}
	
	skiplist_node ** nodes = skiplist_search_all(sl, score, &matches);
	
	for(i = 0;i<matches;i++)
	{
		if(filter)
		{
			if(sl->match)
			{
				if(sl->match(nodes[i]->obj, filter))
					s_queue_push(queue, nodes[i]->obj);
			}
			else{
				if(nodes[i]->obj == filter)
					s_queue_push(queue, nodes[i]->obj);
			}
		}
	}

	if(*count = queue->matches)
	{
		*search_result = queue->objs;
	}
	else{
		free(queue->objs);
		*search_result = NULL;
		
	}

	free(queue);
}

2.5 跳跃表的插入

在插入时首先确定要占据的层数K，这里通常会用到如下两种方法：

抛硬币方式：即采用类似于抛硬币的方式，只要是正面就累加，直到遇到反面才停止，最后记录正面的次数并将其作为要添加新元素的层。

int get_random_level()
{
	int level = 1;

	while(random() % 2)
		level++;

	if(level > MAX_LEVEL)
		level = MAX_LEVEL;
	return level;
}

统计概率方式：先给定一个概率p,产生一个0到1之间的随机数，如果这个随机数小于p，则将高度加1，直到产生的随机数大于概率p才停止，根据给出的结论，当概率为1/2或者1/4的时候，整体的性能会比较好（其实当p=1/2时，也就是抛硬币的方法）

int get_random_level(double p)
{
	int level = 1;
	double convert = p * RANDMAX;

	while((double)random() < convert)
		level++;
	
	if(level > MAX_LEVEL)
		level = MAX_LEVEL;

	return level;
}

确定好层数K之后，然后在level 1...level K各个层的链表都插入元素。参看如下示例：

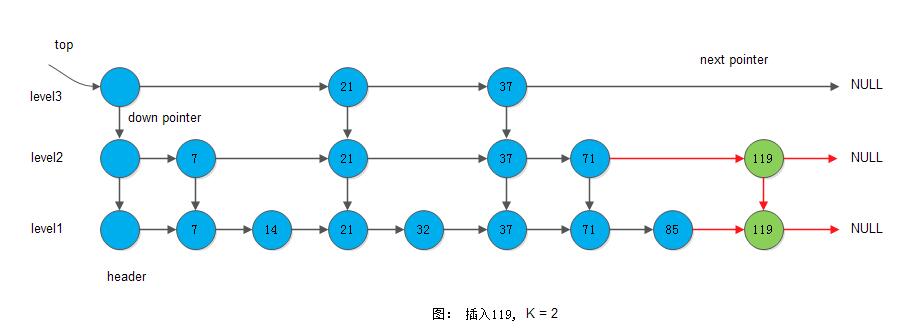
1）插入119， K=2

下图显示在插入119， K=2时的情形：

ds-skiplist-insert1

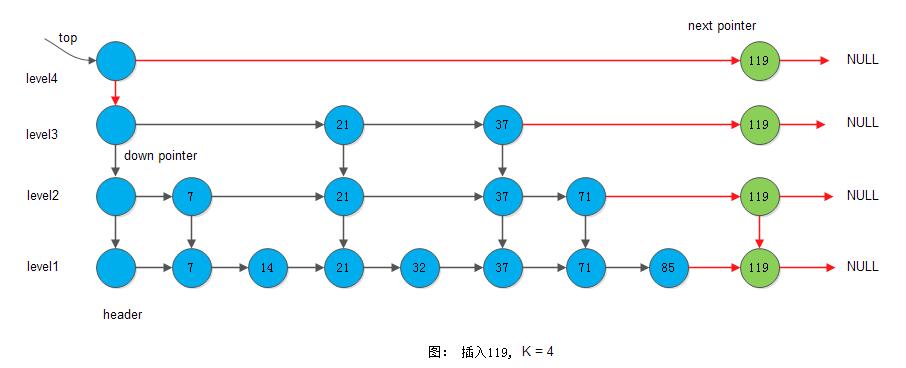
2) 插入119, K=4

下图显示在插入119， K=2时的情形：

ds-skiplist-insert2

下面我们给出跳跃表插入算法：

int get_random_level(double p)
{
	int level = 1;
	double convert = p * RAND_MAX;

	while((double)random() < convert)
		level++;

	if(level > SKIPLIST_MAX_LEVEL)
		level = SKIPLIST_MAX_LEVEL;

	return level;
}

//本函数用于找出小于等于node->score，离node距离最近且level高度各不相等的节点
static void skiplist_get_update(skiplist *sl, skiplist_node *node, skiplist_node ***update)
{
	int max_level = SKIPLIST_MAX_LEVEL;
	skiplist_node **update_origin = (skiplist_node **)malloc(sizeof(skiplist_node *) * max_level);
	if(!update_origin)
	{
		*update = NULL;
		return;
	}

	skiplist_node *p = sl->header;
	int i = 0;

	while(i < max_level)
	{
		update_origin[i++] = sl->header;	/*初始值设置为头结点*/
	}

	//search from top to bottom
	for(i = sl->level -1; i>=0;i--)
	{
		while(p->level[i].forward && (p->level[i].forward->score <= node->score))
		{
			p = p->level[i].forward;
		}

		update_origin[i] = p;
	}

	*update = update_origin;
}



/*
 * Insert status code
 *
 * insert success/refuse(has the same node)/insert failure
 */
#define INSERT_CODE_SUCCESS 1
#define INSERT_CODE_REFUSE  2
#define INSERT_CODE_FAILURE -1

int skiplist_insert(skiplist *sl, double score, void *obj)
{
	int i;
	int matches;
	void **search_result = NULL;
	skiplist_search(sl,score, &matches, obj,&search_result);
	if(matches > 0)
	{
		free(search_result);
		return INSERT_CODE_REFUSE;		/*duplicated node*/
	}

	int level = get_random_level(0.25);
	skiplist_node *node = create_skiplist_node(level, score, obj);
	skiplist_node **update = NULL;		/*存放每一层插入节点*/

	skiplist_get_update(sl,node,&update);
	if(!update)
		return INSERT_CODE_FAILURE;

	//insert from top to bottom
	for(i = level -1; i>=0;i--)
	{
		node->level[i].forward = update[i]->level[i].forward;
		update[i]->level[i].forward = node;
	}

	//update backward
	//if backward node is header,then set it to NULL
	node->backward = (update[0] == sl->header) ? NULL : update[0];

	//update node
	if(node->level[0].forward)
		node->level[0].forward->backward = node;
	else
		sl->tail = node;

	//update the skiplist's maxt level
	if(sl->level < level)
		sl->level = level;

	sl->length++;

	//free update
	free(update);
	return INSERT_CODE_SUCCESS;
}

2.6 跳跃表的删除

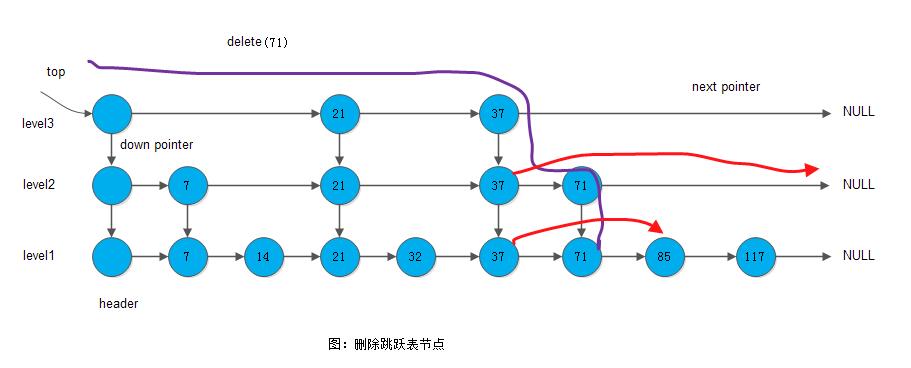
在各个层中找到包含x的节点，使用标准的delete from list方法删除该节点。请参看下图删除71:

ds-skiplist-delete

下面给出相应的代码实现：

static void skiplist_get_update_new(skiplist *sl, skiplist_node *node, skiplist_node ***update)
{
	int max_level = SKIPLIST_MAX_LEVEL;
	skiplist_node **update_origin = (skiplist_node **)malloc(sizeof(skiplist_node *)*max_level);
	if(!update_origin)
	{
		*update = NULL;
		return;
	}

	skiplist_node *p = sl->header;
	int i = 0;
	while(i < max_level)
	{
		update_origin[i++] = sl->header;   //init update_origin
	}

	for(i = sl->level-1;i>=0;i--)
	{
		while(p->level[i].forward && (p->level[i].forward->score <= node->score))
		{
			if(p->level[i].forward->score == node->score)
			{
				if(sl->match)
				{
					if(sl->match(node->obj,p->level[i].forward->obj))
						break;
				}
				else{
					if(node->obj == p->level[i].forward->obj)
						break;
				}
			}

			p = p->level[i].forward;
		}

		update_origin[i] = p;
	}

	*update = update_origin;
}


static void skiplist_remove_node(skiplist *sl, skiplist_node *node)
{
	if(!node)
		return;

	skiplist_node *pre = node->backward;
	skiplist_node *next = node->level[0].forward;

	if(pre)
	{
		int i;

		//update 'pre' node
		skiplist_node **update = NULL;
		skiplist_get_update_new(sl, node, &update);
		if(!update)
			return;

		for(i = node->levels-1;i>=0;i--)
		{
			update[i]->level[i].forward = node->level[i].forward;
		}

		//update 'next'
		if(next)
			next->backward = pre;
		else
			sl->tail = pre;

		//update the node's level, tranverse the skiplist
		#if 0
			if(node->levels >= sl->level)
			{
				skiplist_node *p = sl->header;
				while(p->level[0].forward)
				{
					if(p->level[0].forward->levels > sl->level)
						sl->level = p->level[0].forward->levels;
					p = p->level[0].forward;
				}
			}
		#else
			//the following is more efficient
			for(i = sl->level-1;i>=0;i--)
			{
				if(sl->header->level[i].forward == NULL)
					sl->level--;
			}
		#endif
			sl->length--;

			if(sl->free)
			sl->free(node->obj);
			free(node);
	}

}


void skiplist_remove(skiplist *sl, double score, int *count, void *filter)
{
	int matches;
	int i;
	skiplist_node **nodes = skiplist_search_all(sl,score, &matches);

	for(i = 0;i<matches;i++)
	{
		/*如果传递了过滤的对象,则根据这个对象来进行过?/
		if(filter)
		{
			if(sl->match)
			{
				if(sl->match(nodes[i]->obj, filter))
					skiplist_remove_node(sl, nodes[i]);
			}
			else{
				if(nodes[i]->obj == filter)
					skiplist_remove_node(sl, nodes[i]);
			}
		}
		else{
			skiplist_remove_node(sl, nodes[i]);
		}
	}
}

2.7 跳跃表的销毁

如下给出跳跃表销毁代码：

/*
 * Description: destroy skip list
 */
void skiplist_destroy(skiplist *sl)
{
	skiplist_node *p = sl->header->level[0].forward;
	skiplist_node *next;

	while(p)
	{
		next = p->level[0].forward;
		if(sl->free)
			sl->free(p->obj);
		free(p);
		p = next;
	}

	free(sl->header);
	free(sl);
}

3. 跳跃表完整实现

下面我们给出跳跃表的完整实现代码。分为如下三个部分：

头文件（skiplist.h)
源文件(skiplist.c)
测试文件(skiplist_test.c)

3.1 跳跃表实现头文件

如下是头文件skiplist.h:

#ifndef __SKIPLIST_H_
#define __SKIPLIST_H_
#include <stdio.h>
#include <stdlib.h>

typedef struct skiplist_node{
	double score;
	void *obj;
	struct skiplist_node *backward;

	int levels;
	struct skiplist_node_level{
		struct skiplist_node *forward;
		//unsigned int span;
	}level[];
}skiplist_node;

typedef struct skiplist{
	struct skiplist_node *header;
	struct skiplist_node *tail;

	int level;
	int length;

	void (*free)(void *obj);
	int (*match)(void *obj1, void *obj2);
}skiplist;

#define SKIPLIST_MAX_LEVEL 32


skiplist *skiplist_create();
#define skiplist_is_empty(sl)       ((sl)->length==0)
#define skiplist_max_level(sl)      ((sl)->level)


/*
 * Description: insert
 * 1: score 可以相同
 * 2: score和obj都相同则拒绝插入
 */
int skiplist_insert(skiplist *sl, double score, void *obj);

/*
 * Description: search by score
 *  1: 如果没有过滤 返回score相同所有obj
  * 2: 如果加了filter过滤， 则返回与filter匹配的结果(match返回1)
 */
void skiplist_search(skiplist *sl, double score, int *count, void *filter, void ***search_result);

/*
 * Description: remove node by score
 * 1: 如果没有过滤 返回score相同所有obj
 * 2: 如果加了filter过滤, 则返回与filter匹配的结果(match返回1)
 */
void skiplist_remove(skiplist *sl, double score, int *count, void *filter);


/*
 * Description: destroy skiplist
 */
void skiplist_destroy(skiplist *sl);


/*
 * Description: Get the first N elements in skip list
 */
void skiplist_first_n(skiplist *sl, int n, int *count, void ***objs);


/*
 * Description: Get the last N elements in skip list
 */
void skiplist_last_n(skiplist *sl, int n, int *count, void ***objs);



//set skiplist destroy function
#define skiplist_set_free(sl,func)   ((sl)->free = func)

//set skiplist match function
#define skiplist_set_match(sl,func)  ((sl)->match=func)



/*
 * Description: print skiplist status
 */
void skiplist_status(skiplist *sl);


#endif

3.2 跳跃表实现源文件

如下是头文件skiplist.c:

#include "skiplist.h"


//For internal use
typedef struct s_queue{
	int matches;
	int slots;
	void **objs;
}s_queue;

s_queue *s_queue_init()
{
	int slots = 4;
	s_queue *queue = (s_queue *)malloc(sizeof(s_queue));
	if(!queue)
		return NULL;
	queue->objs = (void **)malloc(sizeof(void *)*slots);
	if(!queue->objs)
	{
		free(queue);
		return NULL;
	}
	queue->slots = slots;
	queue->matches = 0x0;
	return queue;
}

int s_queue_push(s_queue *queue, void *obj)
{
	if(queue->matches >= queue->slots)
	{
		int slots = queue->slots >> 1;
		void **objs = (void **)realloc(queue->objs, slots * sizeof(void *));
		if(!objs)
			return -1;

		queue->objs = objs;
		queue->slots = slots;
	}

	queue->objs[queue->matches++] = obj;
	return 0x0;

}



// create skiplist node
skiplist_node *create_skiplist_node(int levels, double score, void *obj)
{
	skiplist_node *node = (skiplist_node *)malloc(sizeof(skiplist_node) + levels * sizeof(struct skiplist_node_level));
	if(!node)
		return NULL;

	node->levels = levels;
	node->score = score;
	node->obj = obj;
	node->backward = NULL;

	while(levels)
	{
		node->level[--levels].forward = NULL;
	}

	return node;

}


//Init skiplist
skiplist *skiplist_create()
{
	skiplist *sl = (skiplist *)malloc(sizeof(skiplist));
	if(!sl)
		return NULL;
	sl->header = create_skiplist_node(SKIPLIST_MAX_LEVEL,0.0,NULL);
	if(!sl->header)
	{
		free(sl);
		return NULL;
	}

	sl->tail = NULL;
	sl->level = 0x0;
	sl->length = 0x0;
	sl->free = NULL;
	sl->match = NULL;

	srandom(time(0));   //for later used
	return sl;
}

static skiplist_node **skiplist_search_all(skiplist *sl, double score, int *count)
{
	int i;
	skiplist_node *p = sl->header;
	skiplist_node **result = NULL;
	s_queue *queue = s_queue_init();
	if(!queue)
		return NULL;

	for(i = sl->level-1; i >= 0; i--)
	{
		while(p->level[i].forward && (p->level[i].forward->score <= score))
		{
			if(p->level[i].forward->score == score)
			{
				s_queue_push(queue, p->level[i].forward);
			}
			p = p->level[i].forward;
		}
	}


	if(*count = queue->matches)
	{
		result = (skiplist_node **)queue->objs;
	}
	else{
		//have no matched object,
		free(queue->objs);
	}
	free(queue);

	return result;
}


void skiplist_search(skiplist *sl, double score, int *count, void *filter, void ***search_result)
{
	int matches = 0x0;
	int i;
	s_queue *queue = s_queue_init();
	if(!queue)
	{
		*count = 0;
		*search_result = NULL;
		return;
	}

	skiplist_node ** nodes = skiplist_search_all(sl, score, &matches);

	for(i = 0;i<matches;i++)
	{
		if(filter)
		{
			if(sl->match)
			{
				if(sl->match(nodes[i]->obj, filter))
					s_queue_push(queue, nodes[i]->obj);
			}
			else{
				if(nodes[i]->obj == filter)
					s_queue_push(queue, nodes[i]->obj);
			}
		}
		else{
			s_queue_push(queue, nodes[i]->obj);
		}
	}

	if(*count = queue->matches)
	{
		*search_result = queue->objs;
	}
	else{
		free(queue->objs);
		*search_result = NULL;
	}

	free(queue);
}


int get_random_level(double p)
{
	int level = 1;
	double convert = p * RAND_MAX;

	while((double)random() < convert)
		level++;

	if(level > SKIPLIST_MAX_LEVEL)
		level = SKIPLIST_MAX_LEVEL;

	return level;
}


static void skiplist_get_update(skiplist *sl, skiplist_node *node, skiplist_node ***update)
{
	int max_level = SKIPLIST_MAX_LEVEL;
	skiplist_node **update_origin = (skiplist_node **)malloc(sizeof(skiplist_node *) * max_level);
	if(!update_origin)
	{
		*update = NULL;
		return;
	}

	skiplist_node *p = sl->header;
	int i = 0;

	while(i < max_level)
	{
		update_origin[i++] = sl->header;	/*初始值设置为头结点*/
	}

	//search from top to bottom
	for(i = sl->level -1; i>=0;i--)
	{
		while(p->level[i].forward && (p->level[i].forward->score <= node->score))
		{
			p = p->level[i].forward;
		}

		update_origin[i] = p;
	}

	*update = update_origin;
}



/*
 * Insert status code
 *
 * insert success/refuse(has the same node)/insert failure
 */
#define INSERT_CODE_SUCCESS 1
#define INSERT_CODE_REFUSE  2
#define INSERT_CODE_FAILURE -1

int skiplist_insert(skiplist *sl, double score, void *obj)
{
	int i;
	int matches;
	void **search_result = NULL;
	skiplist_search(sl,score, &matches, obj,&search_result);
	if(matches > 0)
	{
		free(search_result);
		return INSERT_CODE_REFUSE;		/*duplicated node*/
	}

	int level = get_random_level(0.25);
	skiplist_node *node = create_skiplist_node(level, score, obj);
	skiplist_node **update = NULL;		/*存放每一层插入节点*/

	skiplist_get_update(sl,node,&update);
	if(!update)
		return INSERT_CODE_FAILURE;

	//insert from top to bottom
	for(i = level -1; i>=0;i--)
	{
		node->level[i].forward = update[i]->level[i].forward;
		update[i]->level[i].forward = node;
	}

	//update backward
	//if backward node is header,then set it to NULL
	node->backward = (update[0] == sl->header) ? NULL : update[0];

	//update node
	if(node->level[0].forward)
		node->level[0].forward->backward = node;
	else
		sl->tail = node;

	//update the skiplist's maxt level
	if(sl->level < level)
		sl->level = level;

	sl->length++;

	//free update
	free(update);
	return INSERT_CODE_SUCCESS;

}



static void skiplist_get_update_new(skiplist *sl, skiplist_node *node, skiplist_node ***update)
{
	int max_level = SKIPLIST_MAX_LEVEL;
	skiplist_node **update_origin = (skiplist_node **)malloc(sizeof(skiplist_node *)*max_level);
	if(!update_origin)
	{
		*update = NULL;
		return;
	}

	skiplist_node *p = sl->header;
	int i = 0;
	while(i < max_level)
	{
		update_origin[i++] = sl->header;   //init update_origin
	}

	for(i = sl->level-1;i>=0;i--)
	{
		while(p->level[i].forward && (p->level[i].forward->score <= node->score))
		{
			if(p->level[i].forward->score == node->score)
			{
				if(sl->match)
				{
					if(sl->match(node->obj,p->level[i].forward->obj))
						break;
				}
				else{
					if(node->obj == p->level[i].forward->obj)
						break;
				}
			}

			p = p->level[i].forward;
		}

		update_origin[i] = p;
	}

	*update = update_origin;
}


static void skiplist_remove_node(skiplist *sl, skiplist_node *node)
{
	if(!node)
		return;

	skiplist_node *pre = node->backward;
	skiplist_node *next = node->level[0].forward;

	if(pre)
	{
		int i;

		//update 'pre' node
		skiplist_node **update = NULL;
		skiplist_get_update_new(sl, node, &update);
		if(!update)
			return;

		for(i = node->levels-1;i>=0;i--)
		{
			update[i]->level[i].forward = node->level[i].forward;
		}

		//update 'next'
		if(next)
			next->backward = pre;
		else
			sl->tail = pre;

		//update the node's level, tranverse the skiplist
		#if 0
			if(node->levels >= sl->level)
			{
				skiplist_node *p = sl->header;
				while(p->level[0].forward)
				{
					if(p->level[0].forward->levels > sl->level)
						sl->level = p->level[0].forward->levels;
					p = p->level[0].forward;
				}
			}
		#else
			//the following is more efficient
			for(i = sl->level-1;i>=0;i--)
			{
				if(sl->header->level[i].forward == NULL)
					sl->level--;
			}
		#endif
		sl->length--;

		if(sl->free)
			sl->free(node->obj);
		free(node);
	}

}


void skiplist_remove(skiplist *sl, double score, int *count, void *filter)
{
	int matches;
	int i;
	skiplist_node **nodes = skiplist_search_all(sl,score, &matches);

	for(i = 0;i<matches;i++)
	{
		/*如果传递了过滤的对象,则根据这个对象来进行过*/
		if(filter)
		{
			if(sl->match)
			{
				if(sl->match(nodes[i]->obj, filter))
					skiplist_remove_node(sl, nodes[i]);
			}
			else{
				if(nodes[i]->obj == filter)
					skiplist_remove_node(sl, nodes[i]);
			}
		}
		else{
			skiplist_remove_node(sl, nodes[i]);
		}
	}
}

void skiplist_status(skiplist *sl)
{
	skiplist_node *p = sl->header;
	int i = 1;
	printf("skiplist: length=%d, max_level=%d\n",sl->length, sl->level);
	while(p->level[0].forward)
	{
		printf("node[%d], score=%f, level=%d\n", i++, p->level[0].forward->score, p->level[0].forward->levels);
		p = p->level[0].forward;
	}
}

/*
 * Description: get skiplist first N elements
 */
void skiplist_first_n(skiplist *sl, int n, int *count, void ***objs)
{
	skiplist_node *p = sl->header;
	s_queue *queue = s_queue_init();
	if(!queue)
	{
		*count = 0;
		*objs = NULL;
		return;
	}

	while(n--)
	{
		if(p->level[0].forward)
		{
			s_queue_push(queue, p->level[0].forward);
		}
		else{
			break;
		}

		p = p->level[0].forward;
	}

	*count = queue->matches;
	*objs = queue->objs;

	if(queue->matches == 0)
	{
		*objs = NULL;
		free(queue->objs);
	}
	free(queue);
}


/*
 * Description: get skiplist last N elements
 */
void skiplist_last_n(skiplist *sl, int n, int *count, void ***objs)
{
	skiplist_node *p = sl->tail;
	s_queue *queue = s_queue_init();
	if(!queue)
	{
		*count = 0;
		*objs = NULL;
		return;
	}

	while(n--)
	{
		if(p)
		{
			s_queue_push(queue, p);
		}
		else{
			break;
		}
		p = p->backward;
	}

	*count = queue->matches;
	*objs = queue->objs;

	if(queue->matches == 0)
	{
		*objs = NULL;
		free(queue->objs);
	}
	free(queue);
}


/*
 * Description: destroy skip list
 */
void skiplist_destroy(skiplist *sl)
{
	skiplist_node *p = sl->header->level[0].forward;
	skiplist_node *next;

	while(p)
	{
		next = p->level[0].forward;
		if(sl->free)
			sl->free(p->obj);
		free(p);
		p = next;
	}

	free(sl->header);
	free(sl);
}

3.3 跳跃表测试

如下是跳跃表测试代码(注：当前在score相同时，跳跃表插入、搜索等操作有些问题)：

#include <stdio.h>
#include <stdlib.h>
#include "skiplist.h"



typedef struct demo{
	int id;
}demo;

#define MAX_OBJS 40

int match(void *obj_1, void *obj_2)
{
	demo *obj1 = (demo *)obj_1;
	demo *obj2 = (demo *)obj_2;

	return (obj1->id == obj2->id);
}


int main(int argc,char *argv[])
{
	skiplist *sl = skiplist_create();
	skiplist_set_match(sl, match);
	
	demo demo_objs[MAX_OBJS];
	int i;
	
	for(i = 0; i<MAX_OBJS; i++)
	{
		demo_objs[i] = i+1;
		skiplist_insert(sl,i,&demo_objs[i]);
	}
	
	
	//1) find
	printf("search...\n");
	int matches;
	void **search_result;
	skiplist_search(sl, 2, &matches, NULL, &search_result);
	
	printf("matches=%d\n",matches);
	for(i=0; i<matches; i++)
	{
		printf("id: %d\n",((demo*)search_result[i])->id);
	}
	
	if(matches)
	free(search_result);
	printf("\n");
	
	
	//2) delete
	printf("remove 5 elements \n");
	int removes;
	for(i=5; i<10; i++)
		skiplist_remove(sl,i,&removes,NULL);
	
	
	//3) print first 5
	printf("print the first 5 elements\n");
	void **objs;
	skiplist_node  *obj;
	skiplist_first_n(sl,5,&matches,&objs);
	for(i=0;i<matches;i++)
	{
		obj = (skiplist_node*)objs[i];
		printf("%f\n",obj->score);
	}
	printf("\n");
	
	
	//4) print last 5
	printf("print the last 5 element\n");
	skiplist_last_n(sl,5,&matches,&objs);
	for(i=0;i<matches;i++){
		obj = (skiplist_node*)objs[i];
		printf("%f\n",obj->score);
	}
	printf("\n");
	
	
	skiplist_status(sl);
	
	
	//5) destroy
	skiplist_destroy(sl);
}

编译运行：

# gcc -o skiplist_test *.c
# ./skiplist_test 
search...
matches=1
id: 1

remove 5 elements 
print the first 5 elements
0.000000
1.000000
2.000000
3.000000
4.000000

print the last 5 element
19.000000
18.000000
17.000000
16.000000
15.000000

skiplist: length=15, max_level=6
node[1], score=0.000000, level=2
node[2], score=1.000000, level=1
node[3], score=2.000000, level=1
node[4], score=3.000000, level=1
node[5], score=4.000000, level=2
node[6], score=10.000000, level=1
node[7], score=11.000000, level=1
node[8], score=12.000000, level=1
node[9], score=13.000000, level=6
node[10], score=14.000000, level=1
node[11], score=15.000000, level=1
node[12], score=16.000000, level=2
node[13], score=17.000000, level=1
node[14], score=18.000000, level=2
node[15], score=19.000000, level=2

Ivanzz

发上等愿，结中等缘，享下等福；择高处立，寻平处住，向宽处行