By

本章主要介绍一下variable-precision SWAR算法的实现原理，之后再对redis中相关位计数操作的实现做简单说明。

1. variable-precision SWAR算法

variable-precision SWAR算法通常用于统计一个数组中非0位的数量，数学上被称为计算汉明重量（Hamming Weight)。

因为汉明重量经常被用于信息论、编码理论和密码学，所以研究人员针对计算汉明重量开发了多种不同的算法，一些处理器甚至直接带有计算汉明重量的指令，而对于不具备这种特殊指令的普通处理器来说，目前已知效率最好的通用算法为variable-precision SWAR算法，该算法通过一系列位移和位运算操作，可以在常数时间内计算多个字节的汉明重量，并且不需要使用额外的内存。

1.1 算法实现

下面给出的是一个处理32位长度位数的variable-precision SWAR算法实现：

//计算32位二进制的汉明重量
uint32_t swar(uint32_t i)
{
	i = (i & 0x55555555) + ((i >> 1) & 0x55555555);			//步骤1
	i = (i & 0x33333333) + ((i >> 2) & 0x33333333);			//步骤2
	i = (i & 0x0F0F0F0F) + ((i >> 4) & 0x0F0F0F0F);			//步骤3
	i = (i * (0x01010101) >> 24);							//步骤4

	return i;
}

1.2 算法分析

我们对上面算法的实现进行分析。首先看上面几个特殊的16进制数：

ds-bit

下面我们分析每一个步骤：

  • 步骤1
i = (i & 0x55555555) + ((i >> 1) & 0x55555555);

其中: (i & 0x55555555)得到j，j的偶数位全为0，奇数位与i的奇数位相对应； (i >> 1) & 0x55555555)得到q，q的偶数位全为0，奇数位与i的偶数位相对应。

通过上面(i & 0x55555555) + ((i >> 1) & 0x55555555)，即j+q得到z，z第1位和第2位的二进制表示(00或01或10)就是i的第1、2位中值为1的数量。这样z中每两位一组的二进制记录了i中对应的两位上的非0的个数。

其实这一步骤也可以写成:

i = i - ((i >> 1) & 0x55555555)

具体原理如下：

    i           j         i - j
----------------------------------
0 = 0b00    0 = 0b00    0 = 0b00
1 = 0b01    0 = 0b00    1 = 0b01
2 = 0b10    1 = 0b01    1 = 0b01
3 = 0b11    1 = 0b01    2 = 0b10
  • 步骤2
i = (i & 0x33333333) + ((i >> 2) & 0x33333333);

该步中的i即上一步中得到的z，如果该步骤中得到的结果是y，那么y中每四位一组的二进制表示记录了i(原始数据）中对应的四位上的非0的个数。

  • 步骤3
i = (i & 0x0F0F0F0F) + ((i >> 4) & 0x0F0F0F0F);

同上，结果是分成4组，每组8个二进制位来表示。

  • 步骤4
i = (i * (0x01010101) >> 24);

在步骤三计算完成后，其实已经分成4组，每组8个二进制位，只要求出每组上二进制表示的值，相加的结果就是汉明重量。

假如i=0b0010 0101 0110 0000 1010 0001 0001 0110，我们来看一下是如何相乘的：

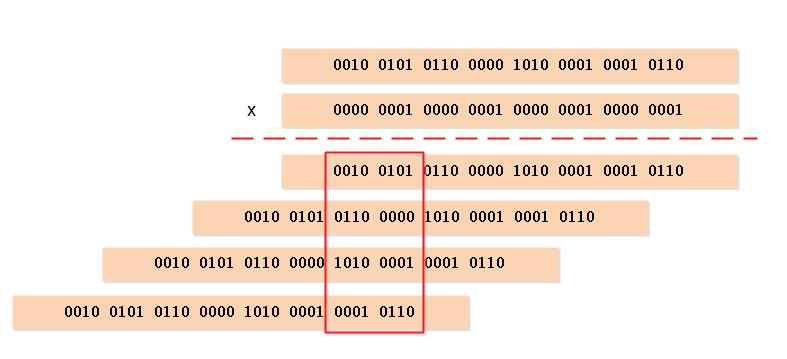
ds-bit

通过上面我们可以看到上面乘法算出的结果刚好是各组中位位1的数目。

2. Redis中求bit count的实现

Redis中求bit count，用到了查表和variable-precision SWAR两种算法：

  • 查表算法使用键长为8位的表，表中记录了从0x00 ~ 0xFF在内的所有二进制位的汉明重量；

  • 至于variable-precision SWAR算法方面，Redis会每次处理128个二进制位，这128个bit会通过调用4次32位variable-precision SWAR算法来计算其汉明重量。

下面给出相应的代码实现：

/* -----------------------------------------------------------------------------
 * Helpers and low level bit functions.
 * -------------------------------------------------------------------------- */

/* Count number of bits set in the binary array pointed by 's' and long
 * 'count' bytes. The implementation of this function is required to
 * work with a input string length up to 512 MB. */
size_t redisPopcount(void *s, long count) {
    size_t bits = 0;
    unsigned char *p = s;
    uint32_t *p4;
	
    static const unsigned char bitsinbyte[256] = {
		0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4,
		1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,
		1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,
		2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
		1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,
		2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
		2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
		3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
		1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,
		2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
		2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
		3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
		2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,
		3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
		3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,
		4,5,5,6,5,6,6,7,5,6,6,7,6,7,7,8
	};

    /* Count initial bytes not aligned to 32 bit. */
    while((unsigned long)p & 3 && count) {
        bits += bitsinbyte[*p++];
        count--;
    }

    /* Count bits 28 bytes at a time */
    p4 = (uint32_t*)p;
    while(count>=28) {
        uint32_t aux1, aux2, aux3, aux4, aux5, aux6, aux7;

        aux1 = *p4++;
        aux2 = *p4++;
        aux3 = *p4++;
        aux4 = *p4++;
        aux5 = *p4++;
        aux6 = *p4++;
        aux7 = *p4++;
        count -= 28;

        aux1 = aux1 - ((aux1 >> 1) & 0x55555555);
        aux1 = (aux1 & 0x33333333) + ((aux1 >> 2) & 0x33333333);
        aux2 = aux2 - ((aux2 >> 1) & 0x55555555);
        aux2 = (aux2 & 0x33333333) + ((aux2 >> 2) & 0x33333333);
        aux3 = aux3 - ((aux3 >> 1) & 0x55555555);
        aux3 = (aux3 & 0x33333333) + ((aux3 >> 2) & 0x33333333);
        aux4 = aux4 - ((aux4 >> 1) & 0x55555555);
        aux4 = (aux4 & 0x33333333) + ((aux4 >> 2) & 0x33333333);
        aux5 = aux5 - ((aux5 >> 1) & 0x55555555);
        aux5 = (aux5 & 0x33333333) + ((aux5 >> 2) & 0x33333333);
        aux6 = aux6 - ((aux6 >> 1) & 0x55555555);
        aux6 = (aux6 & 0x33333333) + ((aux6 >> 2) & 0x33333333);
        aux7 = aux7 - ((aux7 >> 1) & 0x55555555);
        aux7 = (aux7 & 0x33333333) + ((aux7 >> 2) & 0x33333333);
        bits += ((((aux1 + (aux1 >> 4)) & 0x0F0F0F0F) +
                    ((aux2 + (aux2 >> 4)) & 0x0F0F0F0F) +
                    ((aux3 + (aux3 >> 4)) & 0x0F0F0F0F) +
                    ((aux4 + (aux4 >> 4)) & 0x0F0F0F0F) +
                    ((aux5 + (aux5 >> 4)) & 0x0F0F0F0F) +
                    ((aux6 + (aux6 >> 4)) & 0x0F0F0F0F) +
                    ((aux7 + (aux7 >> 4)) & 0x0F0F0F0F))* 0x01010101) >> 24;
    }
	
    /* Count the remaining bytes. */
    p = (unsigned char*)p4;
    while(count--) bits += bitsinbyte[*p++];
	
    return bits;
}



[参看]

  1. variable-precision SWAR算法“计算汉明重量”

  2. variable-precision SWAR算法解析