数据结构之Radix Tree
本文我们简要介绍一下Radix Tree的相关概念及实现原理。
1. radix tree定义
在计算机科学中,radix tree(也被称为radix trie,或者compact prefix tree)用于表示一种空间优化的trie(prefix tree)数据结构。 假如树中的一个节点是父节点的唯一子节点(the only child)的话,那么该子节点将会与父节点进行合并,这样就使得radix tree中的每一个内部节点最多拥有r个孩子, r为正整数且等于2^n(n>=1)。不像是一般的trie树,radix tree的边沿(edges)可以是一个或者多个元素。参看如下:
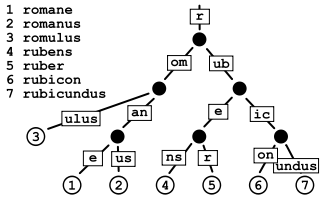
在radix tree的wiki中说到如下场景也很适合使用此数据结构来存储:
This makes radix trees much more efficient for small sets (especially if the strings are long) and for sets of strings that share long prefixes. 即元素个数不是太多,但是元素之间通常有很长的相同前缀时很适合采用radix tree来存储
不像是平常的树结构(在进行key的比较时,是整个key从头到尾进行比较),radix key在每个节点进行key的比较时是以bit组(chunk-of-bits)为单位来进行的,每一个chunk中的bit数目等于radix tree的基数r。
2. radix tree使用场景举例
我们经常使用Radix tree来构建key为字符串的关联数组(associative arrays);在构建IP路由(ip-routing)的应用方面radix tree也使用广泛,因为IP通常具有大量相同的前缀; 另外radix tree在倒排索引方面也使用广泛。
3. radix tree操作
Radix tree支持插入、删除、搜索等方面的操作。插入操作是添加一个新的字符串到trie树中并尝试最小化数据存储(即对某些节点进行合并); 删除操作是从trie树中移除一个字符串; 而搜索操作包括严格查找(exact lookup)、前缀查找、后缀查找以及查询某个前缀的所有字符串。所有这些操作的时间复杂度为O(k)(k为字符串集合中最长的字符串长度)。
3.1 查找
查找操作用于判定一个字符串是否存在于trie树中。本操作与普通的trie树查找相似,除了某些edges可能会包含多个元素之外。
如下的伪代码我们假设这些类已经存在:
Edge
-
Node targetNode
-
string label
Node
-
Array of Edges edges
-
function isLeaf()
关于edge与node的关系,参看如下图示:
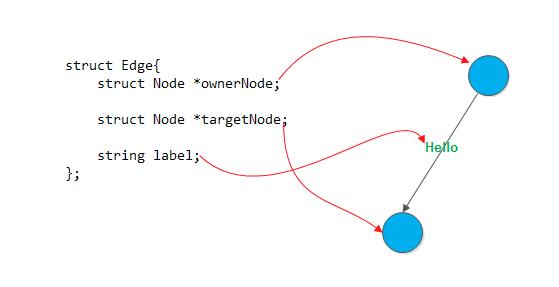
function lookup(string x)
{
// Begin at the root with no elements found
Node traverseNode := root;
int elementsFound := 0;
// Traverse until a leaf is found or it is not possible to continue
while (traverseNode != null && !traverseNode.isLeaf() && elementsFound < x.length)
{
// Get the next edge to explore based on the elements not yet found in x
Edge nextEdge := select edge from traverseNode.edges where edge.label is a prefix of x.suffix(elementsFound)
// x.suffix(elementsFound) returns the last (x.length - elementsFound) elements of x
// Was an edge found?
if (nextEdge != null)
{
// Set the next node to explore
traverseNode := nextEdge.targetNode;
// Increment elements found based on the label stored at the edge
elementsFound += nextEdge.label.length;
}
else
{
// Terminate loop
traverseNode := null;
}
}
// A match is found if we arrive at a leaf node and have used up exactly x.length elements
return (traverseNode != null && traverseNode.isLeaf() && elementsFound == x.length);
}下面给出radix tree查找的一个过程图:
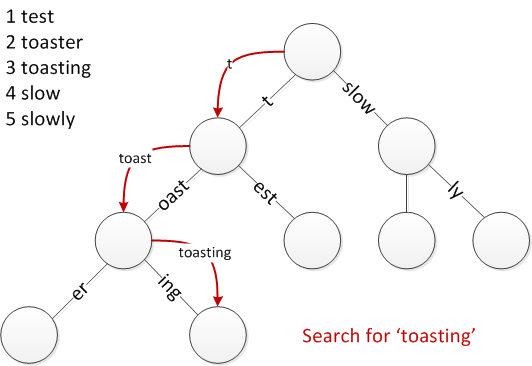
3.2 插入操作
要插入一个字符串,首先我们需要执行查找,直到查找到某个节点处停止。此时,我们或者可以直接将input string的剩余部分添加到一个新的Edge中; 或者有一个edge与我们的input string的剩余部分有相同的前缀,此种情况下我们需要将该edge分裂成两个edge(其中第一个edge存储common prefix)然后再进行处理。这里分裂edge确保了一个节点的孩子(children)数目不会超过总的字符串的个数。
如下我们展示了插入时的多种情况(仍有部分未列出)。下图中r代表的是根节点(root)。这里我们假设edge以空字符串(empty string)作为结尾。
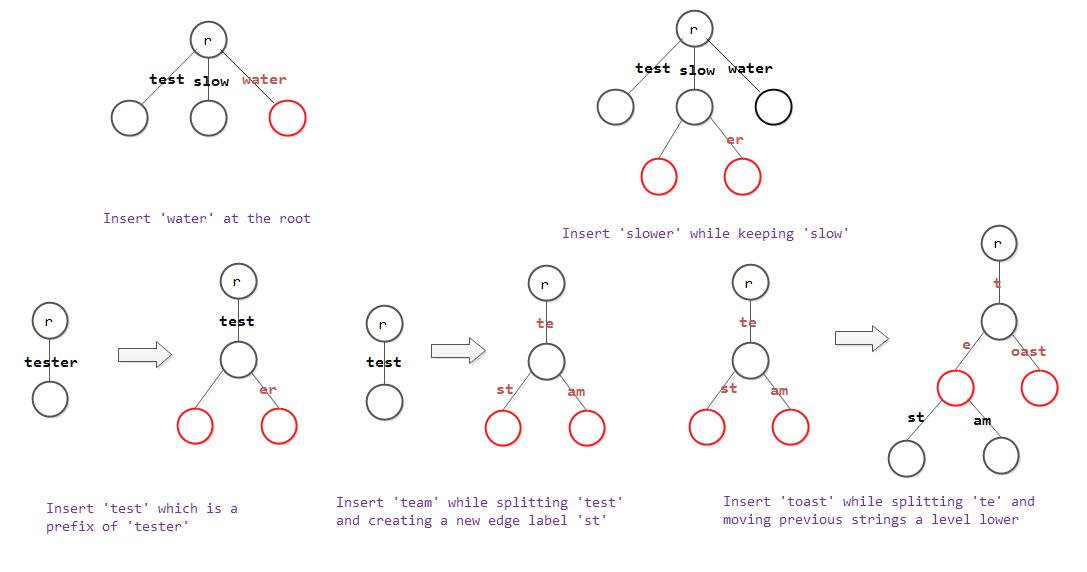
3.3 删除节点
要从radix tree中删除一个字符串x,我们必须首先定位到代表x的叶子节点。假设该叶子节点存在,我们就移除该叶子节点。此时,我们需要检查该被删节点的父节点,假如父节点只剩下一个孩子节点的话,则将该孩子节点的incomming label追加到父节点的incomming label上并将该孩子节点移除。
3.4 与其他数据结构的比较
(说明: 如下的比较,我们假设key的长度为k,数据结构中元素的数目为n)
radix tree允许在O(k)的时间复杂度内进行查找、插入、删除等操作,而balanced trees在进行这些操作时时间复杂度一般为O(logn)。这看起来并不像是一个优势,因为通常情况下k>=log(n),但是在平衡树中key的比较通常是字符串的完整比较,时间复杂度是O(k),并且在实际使用过程中很多key可能还拥有相同的前缀。假如使用trie数据结构来进行存储,所有key的比较都是constant time,但是如果我们查询的字符串长度为m,那么也必须执行m次的比较。使用radix tree数据结构时,则需要更少的比较操作,并且使用的节点个数也更少。
当然,radix tree也与trie树一样有相同的劣势,然而:因为它们只能被应用于字符串元素或者能够高效映射为字符串的元素,它们缺少了平衡查找树那样的通用性,平衡查找树可以应用于任何类型以及任何比较顺序。
而Hashtables通常被认为具有O(1)时间复杂度的插入与删除操作,但先决条件是我们认为计算hash key的操作可以在constant-time内完成。当我们把计算hash key的时间也考虑在内的话,hashtables的插入和删除时间复杂度就变为O(k),并且在key碰撞的情况下,可能会有更差的时间复杂度。radix tree的插入和删除的时间复杂度为O(k)。此外,hashtables也不支持Find predecessor与Find successor操作。
Find predecessor: Locates the largest string less than a given string, by lexicographic order. Find successor: Locates the smallest string greater than a given string, by lexicographic order.
3.5 示例代码
下面我们给出一个radix tree实现的示例代码(注意,这里edges我们并没有按字典序来进行存储):
typedef struct radix_node_s radix_node_t;
struct radix_edge_t{
radix_node_t *incommingNode;
char *label;
struct radix_edge_t *next;
};
struct radix_node_s{
struct radix_edge_t *head;
};
char *global_empty_str = ""
int init_radix_tree(radix_node_t *root)
{
root->head = NULL;
}
int is_leaf(radix_node_t *node)
{
if(node->head == NULL)
return 1;
return 0;
}
/*
* description: check wether 'pre' is prefix of label
*
* return: 0---not prefix 1---is prefix and but not equal 2 --- equal
*/
int is_prefix(char *pre, char *label, char **out)
{
*out = label;
while(*pre && *pre++ == *label++);
if(*pre)
return 0;
else{
*out = label;
if (*label)
return 1;
else
return 2;
}
}
int insert_radix_tree(radix_node_t *root, char *label)
{
radix_node_t *p = root;
radix_node_t *prev = root;
struct radix_edge_t *edge;
char *s = label;
int a;
while(p && !is_leaf(p) && *s){
edge = p->head;
while(edge){
a = is_prefix(edge->label,s, &s);
if(a = 1){
prev = p;
p = edge->incommingNode;
break;
}else if(a == 2){
return 0;
}
edge = edge->next;
}
if (!edge)
break;
}
if (prev->head)
{
struct radix_edge_t *new_edge = (struct radix_edge_t *)malloc(sizeof(struct radix_edge_t));
new_edge.incommingNode = NULL;
new_edge.label = strdup(s);
new_edge.next = prev->head;
prev->head = new_edge;
}else{
struct radix_edge_t *empty_edge = (struct radix_edge_t *)malloc(sizeof(struct radix_edge_t));
struct radix_edge_t *new_edge = (struct radix_edge_t *)malloc(sizeof(struct radix_edge_t));
empty_edge.label = global_empty_str
empty_edge.incommingNode = NULL;
empty_edge.next = new_edge;
new_edge.label = strdup(s);
new_edge.incommingNode = NULL;
new_edge.next = NULL;
prev->head = empty_edge;
}
return 0x0;
}注意,此示例代码给出的数据结构定义并不符合3.1节介绍的结构。本示例设计的数据结构不好,可忽略。
2. Linux基数树
对于长整型数据的映射,怎样解决Hash冲突和Hash表大小的设计是一个非常头疼的问题。radix树就是针对这对这样的稀疏长整型数据查找,能高速且节省空间地完成映射。借助于Radix树,我们能够实现对于长整型数据类型的路由。利用radix树能够依据一个长整型(比如一个长ID)高速的找到其相应的对象指针。这比用hash映射来的简单,也更节省空间,使用Hash映射hash函数难以设计,不恰当的hash函数可能增大冲突,或浪费空间。
radix tree是一种多叉搜索树,树的叶子节点是实际的数据条目。每一个节点有一个固定的、2^n指针指向子节点(每一个指针称为slot,n为划分的基的大小)。
2.1 插入、删除
radix tree事实上就几乎与传统的二叉树相同。仅仅是在寻找方式上,利用比如一个unsigned int类型的每个比特位作为树节点的推断。例如,我们有一个数据:
1000101010101010010101010010101010
那么依照radix树的插入就是在根节点开始,假如遇到0,就指向左节点;遇到1就指向右节点。在插入过程中构造树节点,在删除过程中删除树节点。如果认为有太多的malloc()调用的话,可以采用池化技术,预先分配多个节点。
每一个节点使用1个bit位的话,会使树的高度过高,非叶节点过多。故在实际应用中,每一个节点通常使用多个bit位,但多bit位会使节点的子节点slot变多,增大节点的体积,一般选用2个或4个bit位作为树节点就可以。如下图所示:
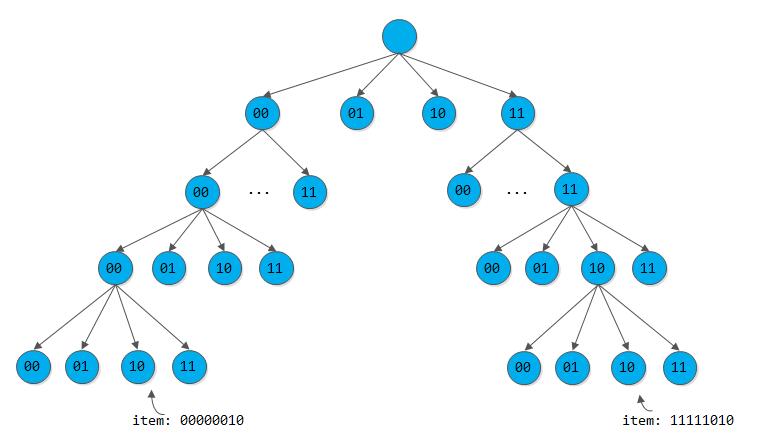
1) 插入
我们在插入一个新节点时,我们依据数据的比特位,在树中向下查找,若没有对应的节点则生成对应节点,直到数据的bit位访问完,则建立叶节点映射对应的对象。
2) 删除
我们可以惰性删除,即沿着路径查找到叶节点后,直接删除叶节点,中间的非叶节点不删除。
2.2 radix树与trie树的比较
Radix树与Trie树的思想有点类似,甚至能够把Trie树看成是一个基为26的Radix树(也可以把radix树看做是Trie树的变异)。Trie树一般用于字符串到对象的映射,而radix树一般用于长整数到对象的映射。
trie树主要问题是树的层高。假设要索引的字符串长度非常长非常变态,我们也要建一颗非常高非常变态的树么? radix树能固定层高(对于较长的字符串,能够用数学公式计算出其特征值,再用radix树存储这些特征值)。
3. Radix树实现示例
如下我们给出一个radix树的实现参考。
1) 头文件
如下是头文件util_radix_tree.h:
#ifndef _UTIL_RADIX_TREE_H_
#define _UTIL_RADIX_TREE_H_
#define MASK32 0xFFFFFFFF
#define MASK64 0xFFFFFFFFFFFFFFFF
void *util_radix_tree_create(int preallocate);
void util_radix_tree_destroy(void *vtree);
int util_radix32tree_insert(void *vtree, uint32_t key, uint32_t mask, uintptr_t value);
int util_radix32tree_delete(void *vtree, uint32_t key, uint32_t mask);
uintptr_t util_radix32tree_find(void *vtree, uint32_t key);
int util_radix64tree_insert(void *vtree, uint64_t key, uint64_t mask, uintptr_t value);
int util_radix64tree_delete(void *vtree, uint64_t key, uint64_t mask);
uintptr_t util_radix64tree_find(void *vtree, uint64_t key);
int util_radix128tree_insert(void *vtree, uint8_t *key, uint8_t *mask, uintptr_t value);
int util_radix128tree_delete(void *vtree, uint8_t *key, uint8_t *mask);
uintptr_t util_radix128tree_find(void *vtree, uint8_t *key);
#endif // _UTIL_RADIX_TREE_H_2) 源文件
如下是源文件util_radix_tree.c:
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#define UTIL_RADIX_NO_VALUE (uintptr_t) -1
typedef struct util_radix_node_s util_radix_node_t;
struct util_radix_node_s {
util_radix_node_t *right;
util_radix_node_t *left;
util_radix_node_t *parent;
uintptr_t value;
};
typedef struct {
util_radix_node_t *root;
util_radix_node_t *free;
} util_radix_tree_t;
int util_radix32tree_insert(void *vtree, uint32_t key, uint32_t mask, uintptr_t value);
static util_radix_node_t *util_radix_alloc(util_radix_tree_t *tree)
{
util_radix_node_t *p;
if (tree->free) {
p = tree->free;
tree->free = tree->free->right;
return p;
}
p = malloc(sizeof(util_radix_node_t));
if (p == NULL) {
return NULL;
}
return p;
}
static void util_radix_free(util_radix_node_t *node)
{
if (node == NULL) {
return;
}
free(node);
}
void *util_radix_tree_create(int preallocate)
{
uint32_t key, mask, inc;
util_radix_tree_t *tree;
tree = malloc(sizeof(util_radix_tree_t));
if (tree == NULL) {
return NULL;
}
tree->free = NULL;
tree->root = util_radix_alloc(tree);
if (tree->root == NULL) {
return NULL;
}
tree->root->right = NULL;
tree->root->left = NULL;
tree->root->parent = NULL;
tree->root->value = UTIL_RADIX_NO_VALUE;
if (preallocate <= 0) {
return tree;
}
mask = 0;
inc = 0x80000000;
while (preallocate--) {
key = 0;
mask >>= 1;
mask |= 0x80000000;
do {
if (util_radix32tree_insert(tree, key, mask, UTIL_RADIX_NO_VALUE)
!= 0)
{
return NULL;
}
key += inc;
} while (key);
inc >>= 1;
}
return tree;
}
static util_radix_node_t *radix_tree_postorder(util_radix_node_t *node)
{
util_radix_node_t *p;
if (NULL != node->left) {
p = radix_tree_postorder(node->left);
if (NULL != p) {
return p;
}
}
if (NULL != node->right) {
p = radix_tree_postorder(node->right);
if (NULL != p) {
return p;
}
}
util_radix_free(node);
return NULL;
}
void util_radix_tree_destroy(void *vtree)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
util_radix_node_t *p;
radix_tree_postorder(tree->root);
while (tree->free) {
p = tree->free;
tree->free = tree->free->right;
util_radix_free(p);
}
}
int util_radix32tree_insert(void *vtree, uint32_t key, uint32_t mask,
uintptr_t value)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
uint32_t bit;
util_radix_node_t *node, *next;
bit = 0x80000000;
node = tree->root;
next = tree->root;
while (bit & mask) {
if (key & bit) {
next = node->right;
} else {
next = node->left;
}
if (next == NULL) {
break;
}
bit >>= 1;
node = next;
}
if (next) {
if (node->value != UTIL_RADIX_NO_VALUE) {
return -3;
}
node->value = value;
return 0;
}
while (bit & mask) {
next = util_radix_alloc(tree);
if (next == NULL) {
return -1;
}
next->right = NULL;
next->left = NULL;
next->parent = node;
next->value = UTIL_RADIX_NO_VALUE;
if (key & bit) {
node->right = next;
} else {
node->left = next;
}
bit >>= 1;
node = next;
}
node->value = value;
return 0;
}
int util_radix32tree_delete(void *vtree, uint32_t key, uint32_t mask)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
uint32_t bit;
util_radix_node_t *node;
bit = 0x80000000;
node = tree->root;
while (node && (bit & mask)) {
if (key & bit) {
node = node->right;
} else {
node = node->left;
}
bit >>= 1;
}
if (node == NULL) {
return -1;
}
if (node->right || node->left) {
if (node->value != UTIL_RADIX_NO_VALUE) {
node->value = UTIL_RADIX_NO_VALUE;
return 0;
}
return -3;
}
for ( ;; ) {
if (node->parent->right == node) {
node->parent->right = NULL;
} else {
node->parent->left = NULL;
}
node->right = tree->free;
tree->free = node;
node = node->parent;
if (node->right || node->left) {
break;
}
if (node->value != UTIL_RADIX_NO_VALUE) {
break;
}
if (node->parent == NULL) {
break;
}
}
return 0;
}
uintptr_t util_radix32tree_find(void *vtree, uint32_t key)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
uint32_t bit;
uintptr_t value;
util_radix_node_t *node;
bit = 0x80000000;
value = UTIL_RADIX_NO_VALUE;
node = tree->root;
while (node) {
if (node->value != UTIL_RADIX_NO_VALUE) {
value = node->value;
}
if (key & bit) {
node = node->right;
} else {
node = node->left;
}
bit >>= 1;
}
return value;
}
int util_radix64tree_insert(void *vtree, uint64_t key, uint64_t mask,
uintptr_t value)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
uint64_t bit;
util_radix_node_t *node, *next;
bit = 0x8000000000000000;
node = tree->root;
next = tree->root;
while (bit & mask) {
if (key & bit) {
next = node->right;
} else {
next = node->left;
}
if (next == NULL) {
break;
}
bit >>= 1;
node = next;
}
if (next) {
if (node->value != UTIL_RADIX_NO_VALUE) {
return -3;
}
node->value = value;
return 0;
}
while (bit & mask) {
next = util_radix_alloc(tree);
if (next == NULL) {
return -1;
}
next->right = NULL;
next->left = NULL;
next->parent = node;
next->value = UTIL_RADIX_NO_VALUE;
if (key & bit) {
node->right = next;
} else {
node->left = next;
}
bit >>= 1;
node = next;
}
node->value = value;
return 0;
}
int util_radix64tree_delete(void *vtree, uint64_t key, uint64_t mask)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
uint64_t bit;
util_radix_node_t *node;
bit = 0x8000000000000000;
node = tree->root;
while (node && (bit & mask)) {
if (key & bit) {
node = node->right;
} else {
node = node->left;
}
bit >>= 1;
}
if (node == NULL) {
return -1;
}
if (node->right || node->left) {
if (node->value != UTIL_RADIX_NO_VALUE) {
node->value = UTIL_RADIX_NO_VALUE;
return 0;
}
return -1;
}
for ( ;; ) {
if (node->parent->right == node) {
node->parent->right = NULL;
} else {
node->parent->left = NULL;
}
node->right = tree->free;
tree->free = node;
node = node->parent;
if (node->right || node->left) {
break;
}
if (node->value != UTIL_RADIX_NO_VALUE) {
break;
}
if (node->parent == NULL) {
break;
}
}
return 0;
}
uintptr_t util_radix64tree_find(void *vtree, uint64_t key)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
uint64_t bit;
uintptr_t value;
util_radix_node_t *node;
bit = 0x8000000000000000;
value = UTIL_RADIX_NO_VALUE;
node = tree->root;
while (node) {
if (node->value != UTIL_RADIX_NO_VALUE) {
value = node->value;
}
if (key & bit) {
node = node->right;
} else {
node = node->left;
}
bit >>= 1;
}
return value;
}
int util_radix128tree_insert(void *vtree, uint8_t *key, uint8_t *mask,
uintptr_t value)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
uint8_t bit;
uint32_t i;
util_radix_node_t *node, *next;
i = 0;
bit = 0x80;
node = tree->root;
next = tree->root;
while (bit & mask[i]) {
if (key[i] & bit) {
next = node->right;
} else {
next = node->left;
}
if (next == NULL) {
break;
}
bit >>= 1;
node = next;
if (bit == 0) {
if (++i == 16) {
break;
}
bit = 0x80;
}
}
if (next) {
if (node->value != UTIL_RADIX_NO_VALUE) {
return -3;
}
node->value = value;
return 0;
}
while (bit & mask[i]) {
next = util_radix_alloc(tree);
if (next == NULL) {
return -1;
}
next->right = NULL;
next->left = NULL;
next->parent = node;
next->value = UTIL_RADIX_NO_VALUE;
if (key[i] & bit) {
node->right = next;
} else {
node->left = next;
}
bit >>= 1;
node = next;
if (bit == 0) {
if (++i == 16) {
break;
}
bit = 0x80;
}
}
node->value = value;
return 0;
}
int util_radix128tree_delete(void *vtree, uint8_t *key, uint8_t *mask)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
uint8_t bit;
uint32_t i;
util_radix_node_t *node;
i = 0;
bit = 0x80;
node = tree->root;
while (node && (bit & mask[i])) {
if (key[i] & bit) {
node = node->right;
} else {
node = node->left;
}
bit >>= 1;
if (bit == 0) {
if (++i == 16) {
break;
}
bit = 0x80;
}
}
if (node == NULL) {
return -1;
}
if (node->right || node->left) {
if (node->value != UTIL_RADIX_NO_VALUE) {
node->value = UTIL_RADIX_NO_VALUE;
return 0;
}
return -1;
}
for ( ;; ) {
if (node->parent->right == node) {
node->parent->right = NULL;
} else {
node->parent->left = NULL;
}
node->right = tree->free;
tree->free = node;
node = node->parent;
if (node->right || node->left) {
break;
}
if (node->value != UTIL_RADIX_NO_VALUE) {
break;
}
if (node->parent == NULL) {
break;
}
}
return 0;
}
uintptr_t util_radix128tree_find(void *vtree, uint8_t *key)
{
util_radix_tree_t *tree = (util_radix_tree_t*)vtree;
uint8_t bit;
uintptr_t value;
uint32_t i;
util_radix_node_t *node;
i = 0;
bit = 0x80;
value = UTIL_RADIX_NO_VALUE;
node = tree->root;
while (node) {
if (node->value != UTIL_RADIX_NO_VALUE) {
value = node->value;
}
if (key[i] & bit) {
node = node->right;
} else {
node = node->left;
}
bit >>= 1;
if (bit == 0) {
i++;
bit = 0x80;
}
}
return value;
}3) 测试文件
如下是测试源文件util_radix_test.c:
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#include "util_radix_tree.h"
#define MASK 0xFFFFFFFF
int main(int argc, char *argv[])
{
void *tree;
int a = 1, b = 2, c = 3, d = 0;
uintptr_t ptr = 0;
int ret;
tree = util_radix_tree_create(0);
ret = util_radix32tree_insert(tree, 1, MASK, (uintptr_t)&a);
ret = util_radix32tree_insert(tree, 2, MASK, (uintptr_t)&b);
ret = util_radix32tree_insert(tree, 3, MASK, (uintptr_t)&c);
ptr = util_radix32tree_find(tree, 1);
printf("**************a:%p, b:%p, c:%p, ptr:%p-%p\n", &a, &b, &c, &ptr, ptr);
ptr = util_radix32tree_find(tree, 2);
printf("**************a:%p, b:%p, c:%p, ptr:%p-%p\n", &a, &b, &c, &ptr, ptr);
ptr = util_radix32tree_find(tree, 3);
printf("**************a:%p, b:%p, c:%p, ptr:%p-%p\n", &a, &b, &c, &ptr, ptr);
util_radix32tree_delete(tree, 3, MASK);
ptr = util_radix32tree_find(tree, 3);
ret = ptr;
if (ret == -1) {
printf("not find\n");
} else {
d = *(int*)ptr;
}
printf("**************a:%p, b:%p, c:%p, d:%d, ptr:%p-%p\n", &a, &b, &c, d, &ptr, ptr);
util_radix_tree_destroy(tree);
return 0;
}编译运行:
# gcc -o util_radix_test util_radix_tree.c util_radix_test.c # ./util_radix_test **************a:0x7ffc5aee9b98, b:0x7ffc5aee9b94, c:0x7ffc5aee9b90, ptr:0x7ffc5aee9b88-0x7ffc5aee9b98 **************a:0x7ffc5aee9b98, b:0x7ffc5aee9b94, c:0x7ffc5aee9b90, ptr:0x7ffc5aee9b88-0x7ffc5aee9b94 **************a:0x7ffc5aee9b98, b:0x7ffc5aee9b94, c:0x7ffc5aee9b90, ptr:0x7ffc5aee9b88-0x7ffc5aee9b90 not find **************a:0x7ffc5aee9b98, b:0x7ffc5aee9b94, c:0x7ffc5aee9b90, d:0, ptr:0x7ffc5aee9b88-0xffffffffffffffff
[参看]:

