数据结构之广义表
本节我们介绍一下广义表的定义及使用。
1. 广义表的定义
顾名思义,广义表是线性表的推广,也有人称其为列表(lists,用复数形式以示与统称的表list的区别)。广泛的用于人工智能等领域的表处理语言LISP语言。把广义表作为基本的数据结构,就连程序也表示为一系列的广义表。
抽象数据类型广义表的定义如下:
ADT GList{
数据对象: D={ei | i=1,2,...,n; n>0; ei∈AtomSet 或ei∈GList,
AtomSet为某个数据对象 }
数据关系: R1={<ei-1,ei> | ei-1,ei∈D, 2<=i<=n}
基本操作:
InitGList(&L);
操作结果: 创建空的广义表L。
CreateGList(&L, S);
初始条件: S是广义表的书写形式串。
操作结果: 由S创建广义表L。
DestroyGList(&L);
初始条件: 广义表L存在
操作结果: 销毁广义表L。
CopyGList(&T, L);
初始条件: 广义表L存在
操作结果: 由广义表L复制得到广义表T。
GListLength(L);
初始条件: 广义表L存在
操作结果: 求广义表L的长度
GListenDepth(L);
初始条件: 广义表L存在
操作结果: 求广义表L的深度
GListEmpty(L);
初始条件: 广义表L存在
操作结果: 判定广义表L是否为空
GetHead(L);
初始条件: 广义表L存在
操作结果: 取广义表L的头
GetTail(L);
初始条件: 广义表L存在
操作结果: 取广义表L的尾
InsertFirst_GL(&L, e);
初始条件: 广义表L存在
操作结果: 插入元素e作为广义表L的第一元素
DeleteFirst_GL(&L, &e);
初始条件: 广义表L存在
操作结果: 删除广义表L的第一元素,并用e返回其值
Traverse_GL(L, Visit());
初始条件: 广义表L存在
操作结果: 遍历广义表L,用函数Visit处理每个元素
}ADT GList;广义表一般记作:
LS = (α1, α2, ..., αn)其中,LS是广义表(α1, α2, …, αn)的名称,n是它的长度。在线性表的定义中, ai(1≤i≤n)只限于是单个元素。而在广义表的定义中,αi可以是单个元素,也可以是广义表,分别称为广义表LS的原子和子表。习惯上,用大写字母表示广义表的名称,用小写字母表示原子。当广义表LS非空时,称第一个元素α1为LS的表头(Head),称其余元素组成的表(α2, α3, …, αn)是LS的表尾(Tail)。
显然,广义表的定义是一个递归的定义,因为在描述广义表时又用到了广义表的概念。下面举一些广义表的例子。
(1) A = () ------- A是一个空表,它的长度为零 (2) B = (e) ------- 列表B只有一个原子e,B的长度为1 (3) C = (a, (b, c, d)) ------- 列表C的长度为2,两个元素分别为原子a和子表(b,c,d) (4) D = (A, B, C) -------- 列表D的长度为3, 其3个元素都是列表。显然,将子表的值代入后,择优D=((),(e), (a,(b,c,d))) (5) E = (α, E) ------- 这是一个递归的表,它的长度为2。 E相当于一个无限的列表E=(α, (α, (α, ...)))
从上述的定义和例子可推出列表的3个重要结论:
1) 列表的元素可以是子表,而子表的元素还可以是子表……由此,列表是一个多层次的结构,可以用图形象地表示。例如图5.7表示的列表D。图中以圆圈表示列表,以方块表示原子。
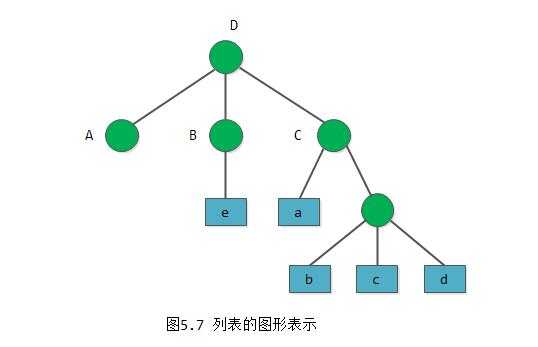
2) 列表可为其他列表所共享。例如,在上述例子中,列表A、B、C为D的子表,则在D中可以不必列出子表的值,而是通过子表的名称来引用。
3) 列表可以是一个递归的表,即列表也可以是其本身的一个子表。例如,列表E就是一个递归的表。
根据前述对表头、表尾的定义可知: 任何一个非空列表其表头可能是原子,也可能是列表,而其表尾必定为列表。例如:
GetHead(B) = e, GetTail(B) = () GetHead(D) = A, GetTail(D) = (B, C)
由于B、C为非空列表,则可以继续分解得到:
GetHead((B, C)) = B, GetTail((B, C)) = (C)
值得提醒的是列表()和(())不同。前者为空表,长度n=0;后者长度n=1,可分解得到其表头、表尾均为空表()。
2. 广义表的存储结构
由于广义表(α1, α2, …, αn)中的数据元素可以具有不同的结构(或是原子,或是列表),因此难以用顺序存储结构表示,通常采用链式存储结构,每个数据元素可用一个结点表示。
如何设定结点的结构?由于列表中的数据元素可能为原子或列表, 由此需要两种结构的结点: 一种是表结点,用于表示列表;一种是原子结点,用以表示原子。从上节得知,若列表不空,则可分解成表头和表尾;反之,一对确定的表头和表尾可唯一确定列表。由此,一个表结点可由3个域组成: 标志域、指示表头的指针域和指示表尾的指针域; 而原子结点只需两个域: 标志域和值域(如图5.8所示)。
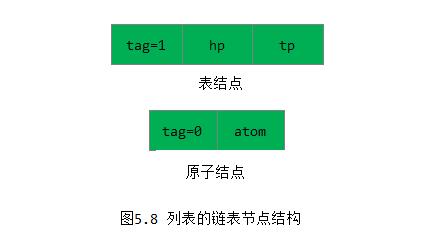
其形式定义说明如下:
//------ 广义表的头尾链表存储表示 -------
typedef enum{
ATOM, //ATOM == 0: 原子
LIST //LIST == 1: 子表
}ElemTag;
typedef GLNode{
ElemTag tag; //公共部分,用于区分原子结点和表结点
union{ //原子结点和表结点的联合部分
AtomType atom; //atom是原子结点的值域,AtomType由用户定义
struct{
struct GLNode *hp;
struct GLNode *tp;
}ptr; //ptr是表节点的指针域,ptr.hp和ptr.tp分别指向表头和表尾
}
}*GList; //广义表类型上节中曾列举了广义表的例子,它们的存储结构如图5.9所示。
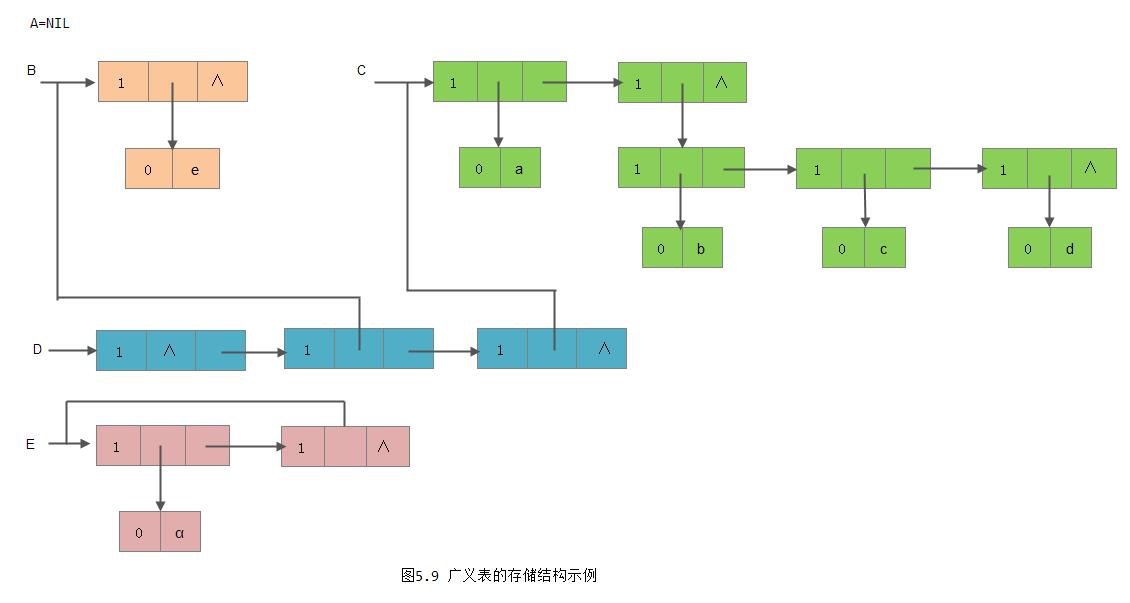
在这种存储结构中有几种情况:
1) 除空表的表头指针为空外,对任何非空列表,其表头指针均指向一个表结点,且该结点中的hp域指示列表表头(或为原子结点,或为表结点),tp域指向列表表尾(除非表尾为空,则指针为空,否则必为表结点);
2)容易分清列表中原子和子表所在层次。如在列表D中,原子a和e在同一层次上,而b、c和d在同一层次且比a和e低一层, B和C是同一层的子表;
3) 最高层的表节点个数即为列表的长度。
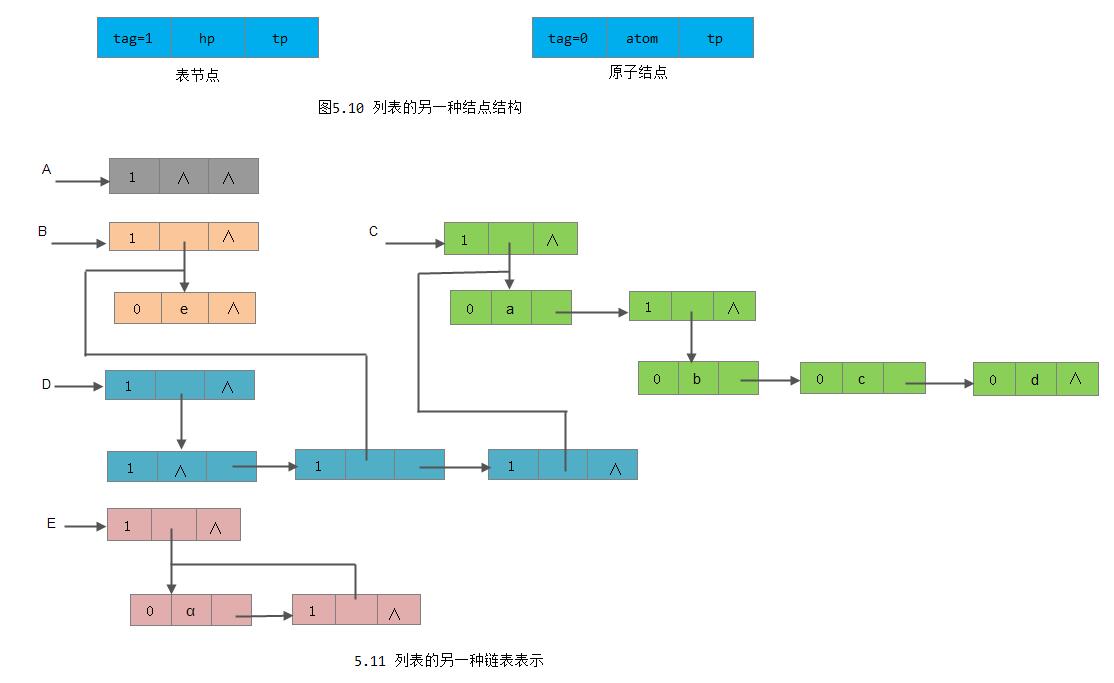
以上3个特点在某种程度上给列表的操作带来方便。也可采用另一种节点结构的链表表示列表,如图5.10和图5.11所示。其形式定义说明如下:
//------ 广义表的扩展线性链表存储表示 -------
typedef enum{
ATOM, //ATOM == 0: 原子
LIST //LIST == 1: 子表
}ElemTag;
typedef GLNode{
ElemTag tag; //公共部分,用于区分原子结点和表结点
union{ //原子结点和表结点的联合部分
AtomType atom; //atom是原子结点的值域,AtomType由用户定义
struct GLNode *hp; //表结点的表头指针
};
struct GLNode *tp; //相当于线性链表的next,指向下一个元素结点
}*GList; 对于列表的这两种存储结构,读者只要根据自己的习惯掌握其中一种结构即可。
3. m元多项式的表示
在一般情况下使用的广义表多数既非是递归表,也不为其他表所共享。对广义表可以这样来理解,广义表中的一个数据元素可以是另一个广义表,一个m元多项式的表示就是广义表的这种应用的典型实例。
在第2章中,我们曾作为线性表的应用实例讨论了一元多项式,一个一元多项式可以用一个长度为m且每个数据元素有两个数据项(系数项和指数项)的线性表来表示。
这里,将讨论如何表示m元多项式。一个m元多项式的每一项最多有m个变元。如果用线性表来表示,则每个数据元素需要m+1个数据项,以存储一个系数值和m个指数值。这将产生两个问题: 一是无论多项式中各项的变元数是多少,若都按m个变元分配存储空间,则将造成浪费;反之,若按各项实际的变元数分配存储空间,就会造成节点的大小不均,给操作带来不便。二是对m值不同的多项式,线性表中的结点大小也不同,这同样会引起存储管理的不便。因此,由于m元多项式中每一项的变化数目的不均匀性和变元信息的重要性,故不适于用线性表表示。例如三元多项式:

情况就不同了。现在,我们再来看这个多项式P,它是变元z的多项式,即Az² + Bz + 15z,只是其中A和B本身又是一个(x,y)的二元多项式,15是z的零次幂的系数。进一步考察A(x,y),又可把它看成是y的多项式。Cy³ + Dy²,而其中C和D为x的一元多项式。循此以往,每个多项式都可以看作是一个变量加上若干个系数指数偶对组成。
任何一个m元多项式都可如此做: 先分解出一个主变元,随后再分解出第二个变元,等等。由此,一个m元的多项式首先是它的主变元的多项式,而其系数又是第二变元的多项式,由此可用广义表来表示m元多项式。例如上述三元多项式可用式(5-7)的广义表表示,广义表的深度即为变元个数。
P = z((A,2), (B, 1), (15, 0)) (5-7)
其中:
A = y((C,3), (D,2))
C = x((1, 10), (2,6))
D = x((3,5))
B = y((E,4), (F,1))
E = x((1,4), (6,3))
F = x((2,0))
可类似于广义表的第二种存储结构来定义表示m元多项式的广义表的存储结构。链表的结点结构为:

其中,exp为指数域,coef为系数域,hp指向其系数子表,tp指向同一层的下一结点。其形式定义说明如下:
typedef struct MPNode{
ElemTag tag; //区分原子结点和表节点
int exp; //指数域
union{
float coef; //系数域
struct MPNode *hp; //表节点的表头指针
};
struct MPNode *tp; //相当于线性链表的next,指向下一个元素节点
}*MPList; //m元多项式广义表类型式(5-7)的广义表的存储结构如图5.12所示,在每一层上增设一个表头结点并利用exp指示该层的变元,可用一维数组存储多项式中所有变元,故exp域存储的是该变元在一维数组中的下标。头指针p所指表结点中的exp的值3为多项式中变元的个数。可见,这种存储结构可表示任何元的多项式。
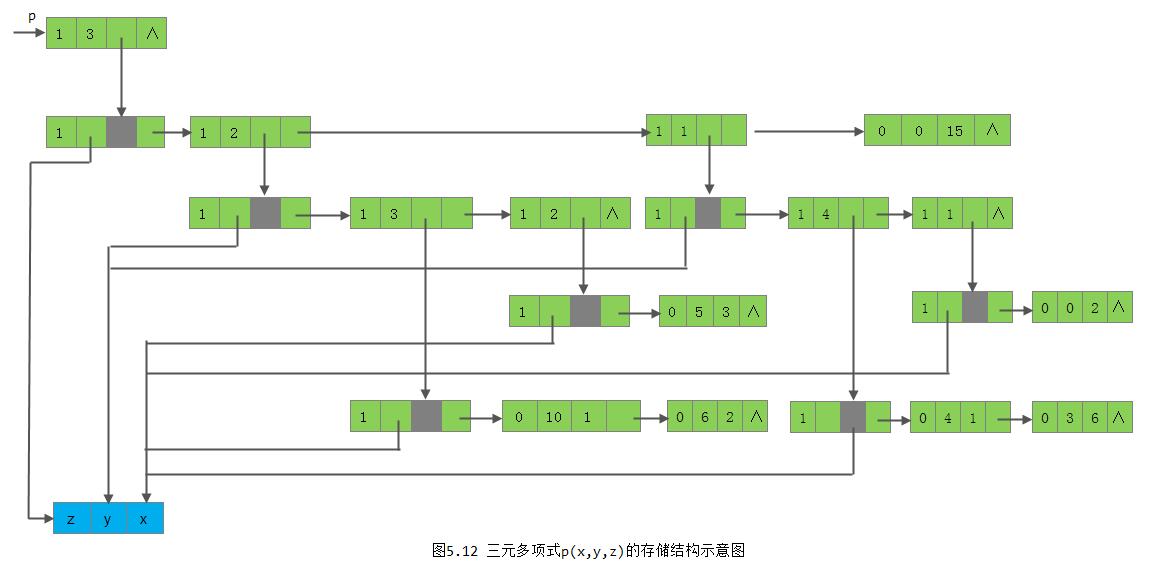
4. 广义表的递归算法
在第3章中曾提及,递归函数结构清晰、程序易读,且容易证明正确性,因此是程序设计的有力工具,但有时递归函数的执行效率很低,因此使用递归应扬长避短。在程序设计的过程中,我们并不一味追求递归。如果一个问题的求解过程有明显的递推规律,我们也很容易写出它的递推过程(如求阶乘函数f(n)=n!的值),则不必要使用“递归”。反之,在对问题进行分解、求解的过程中得到的是和原问题性质相同的子问题(如Hanoi塔问题),由此自然得到一个递归算法,且它比利用栈实现的非递归算法更符合人们的思维逻辑,因而更易于理解。但是要熟练掌握递归算法的设计方法也不是件轻而易举的事情。在本节中,我们不打算全面讨论如何设计递归算法,只是以广义表为例,讨论如何利用“分治法”(Divide and Conquer)进行递归算法设计的方法。
对这类问题设计递归算法时,通常可以先写出问题求解的递归定义。和第二数学归纳法类似,递归定义由基本项和归纳项两部分组成。
递归定义的基本项描述了一个或几个递归过程的终结状态。虽然一个有限的递归(且无明显的迭代)可以描述一个无限的计算过程,但任何实际应用的递归过程,除错误情况外,必定能经过有限层次的递归而终止。所谓终结状态指的是不需要继续递归而可直接求解的状态。例如3-3的n阶Hanio问题,在n=1时可以直接求得解,即将圆盘从X塔座移动到Z塔座上。一般情况下,若递归参数为n,则递归的终结状态为n=0或n=1等。
递归定义的归纳项描述了如何实现从当前状态到终结状态的转化。递归设计的实质是:当一个复杂的问题可以分解成若干子问题来处理时,其中某些子问题与原问题有相同的特征属性,则可利用和原问题相同的分析处理方法;反之,这些子问题解决了,原问题也就迎刃而解了。递归定义的归纳项就是描述这种原问题和子问题之间的转化关系。仍以Hanoi塔问题为例。原问题是将n个圆盘从X塔座移至Z塔座上,可以把它分解成3个子问题:
(1) 将编号为1至n-1的n-1个圆盘从X塔座移至Y塔座; (2) 将编号为n的圆盘从X塔座移至Z塔座; (3) 将编号为1至n-1的圆盘从Y塔座移至Z塔座。
其中(1)和(3)的子问题和原问题特征属性相同,只是参数(n-1和n)不同,由此实现了递归。
由于递归函数的设计用的是归纳思维的方法,则在设计递归函数时,应注意: 1) 首先应书写函数的首部和规格说明,严格定义函数的功能和接口(递归调用的界面),对求精函数中所得的和原问题性质相同的子问题,只要接口一致,便可进行递归调用;2) 对函数中的每一个递归调用都看成只是一个简单的操作,只要接口一致,必能实现规格说明中定义的功能,切忌想的太深太远。正如用第二数学归纳法证明命题时,由归纳假设进行归纳证明时,决不能怀疑归纳假设是否正确。
下面讨论广义表的3种操作。首先约定所讨论的广义表都是非递归表且无共享子表。
4.1 求广义表的深度
广义表的深度定义为广义表中括弧的重数,是广义表的一种量度。例如,多元多项式广义表的深度为多项式中变元的个数。
设非空广义表为:
LS = (α1, α2, ..., αn)
其中αi(i=1,2,…,n)或为原子或为LS的子表,则求LS深度可分解为n个子问题,每个子问题为求αi的深度,若αi为原子,则由定义其深度为零,若ai是广义表,则和上述一样处理,而LS的深度为各αi(i=1,2,…,n)的深度中最大值加1。空表也是广义表,并由定义可知空表的深度为1。
由此可见,求广义表的深度的递归算法有两个终结状态:空表和原子,且只要求得αi(i=1,2,…,n)的深度,广义表的深度就容易求得了。显然,它应比子表深度的最大值多1。
广义表
LS = (α1, α2, ..., αn)
的深度DEPTH(LS)的递归定义为:
基本项: DEPTH(LS) = 1 当LS为空表时
DEPTH(LS) = 0 当LS为原子时
归纳项: DEPTH(LS) = 1 + Max{DEPTH(αi)} n≥1
1≤i≤n由此定义容易写出求深度的递归函数。假设L是GList型的变量,则L=NULL表明广义表为空表,L->tag = 0表明是原子。反之,L指向表节点,该节点中的hp指针指向表头,即为L的第一个子表,而结点中的tp指针所指表尾结点中的hp指针指向L的第二个子表。在第一层中由tp相连的所有尾结点中的hp指针均指向L的子表。由此,求广义表深度的递归函数如算法5.5所示。
算法5.5
int GListDepth(GList L)
{
//采用头尾链表存储结构,求广义表L的深度
if(!L)
return 1; //空表深度为1
if(L->tag == ATOM) //原子深度为0
return 0;
for(max = 0, pp = L; pp; pp = pp->ptr.tp){
dep = GListDepth(pp->ptr.hp); //求以pp->ptr.hp为头指针的子表深度
if(dep > max)
max = dep;
}
return max+1; //非空表的深度是各元素的深度的最大值加1
}上述算法的执行过程实质上是遍历广义表的过程,在遍历中首先求得各子表的深度,然后综合得到广义表的深度。例如,图5.13展示了求广义表D的深度的过程。图中用虚线示意遍历过程中指针L的变化状况,在指向节点的虚线旁标记的是将要遍历的子表,而在从结点射出的虚线旁标记的数字是刚求得的子表的深度,从图中可见广义表D=(A,B,C)=((), (e), (a, (b,c,d)))的深度为3。
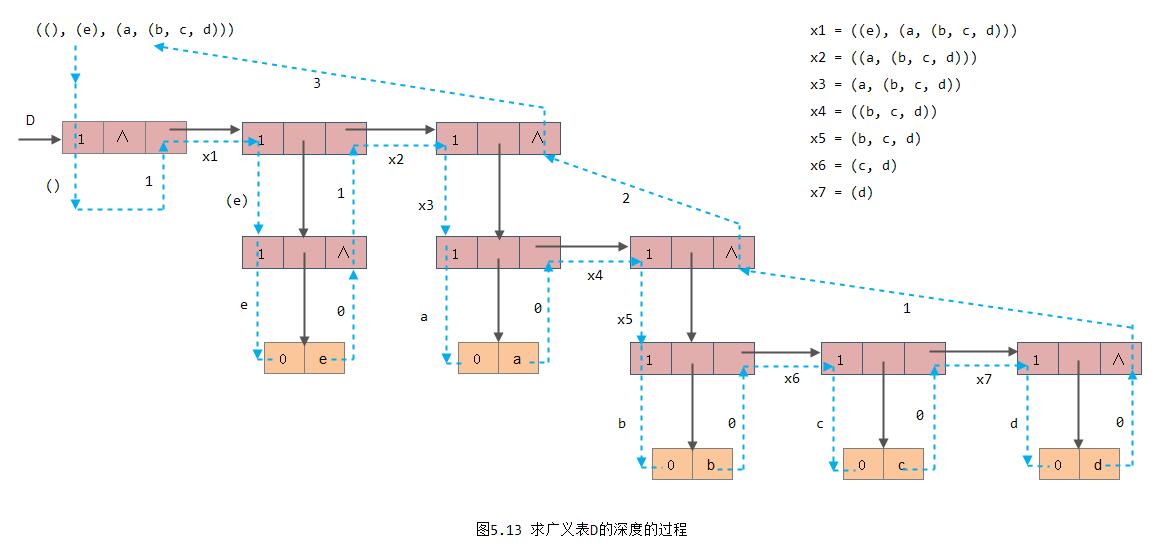
若按递归定义分析广义表D的深度,则有:
DEPTH(D) = 1 + Max{DEPTH(A), DEPTH(B), DEPTH(C)}
DEPTH(A) = 1;
DEPTH(B) = 1 + Max{DEPTH(e)} = 1+0 = 1
DEPTH(C) = 1 + Max{DEPTH(a), DEPTH((b,c,d))} = 2
DEPTH(a) = 0
DEPTH((b,c,d)) = 1 + Max{DEPTH(b), DEPTH(c), DEPTH(d)}
= 1 + 0
= 1由此,DEPTH(D) = 1 + Max{1, 1, 2} = 3。
4.2 复制广义表
在前面的第一节(广义表的定义)中曾提及,任何一个非空广义表均可分解成表头和表尾,反之,一对确定的表头和表尾可唯一确定一个广义表。由此,复制一个广义表只要分别复制其表头和表尾,然后合成即可。假设LS是原表, NEWLS是复制表,则复制操作的递归定义如下。
基本项: InitGList(NEWLS) { 置空表 }, 当LS为空表时。
归纳项: COPY(GetHead(LS) -> GetHead(NEWLS)) { 复制表头 }
COPY(GetTail(LS) -> GetTail(NEWLS)) { 复制表尾 }若原表以图5.9(即: 广义表的头尾链表存储表示)的链表表示,则复制表的操作便是建立相应的链表。只要建立和原表中的结点一一对应的新结点,便可得到复制表的新链表。由此可写出复制广义表的递归算法如算法5.6所示。
算法5.6
Status CopyGList(GList &T, GList L)
{
//采用头尾链表存储结构,由广义表L复制得到广义表T。
if(!L){
T = NULL;
}
else{
if(!(T = (GList)malloc(sizeof(GLNode)))) //建表节点
exit(OVERFLOW);
T->tag = L->tag;
if(L->tag == ATOM){ //复制单原子
T->atom = L->atom;
}
else{
CopyGList(T->ptr.hp, L->ptr.hp); //复制广义表L->ptr.hp的一个副本T->ptr.hp
CopyGList(T->ptr.tp, L->ptr.tp); //复制广义表L->ptr.tp的一个副本T->ptr.tp
}
}
return OK;
}注意,这里使用了变参,使得这个递归函数简单明了,直截了当地反映出广义表的复制过程,读者可尝试以广义表C为例循序查看过程,以便得到更深刻的了解。
4.3 建立广义表的存储结构
从上述两种广义表操作的递归算法的讨论中可以发现: 在对广义表进行的操作下递归定义时,可有两种分析方法。一种是把广义表分解成表头和表尾两部分;另一种是把广义表看成是含有n个并列子表(假设原子也视作子表)的表。在讨论建立广义表的存储结构时,这两种分析方法均可。、
假设把广义表的书写形式看成是一个字符串S,则当S为非空白串时广义表非空。此时可以利用本章第一节中定义的获取列表表头GetHead和获取列表表尾GetTail两个函数建立广义表的链表存储结构。这个递归算法和复制的递归算法极为相似,读者可自行试之。下面就第二种分析方法进行讨论。
广义表字符串S可能有两种情况:
(1) S = '()' (带括弧的空白串); (2) S = (α1, α2, ..., αn),其中αi(i=1,2,...,n)是S的子串
对应于第一种情况S的广义表为空表,对应于第二种情况S的广义表中含有n个子表,每个子表的书写形式即为子串αi(i=1,2,…,n)。此时可类似于求广义表的深度,分析由S建立的广义表和由αi(i=1,2,…,n)建立的子表之间的关系。假设按图5.8所示节点结构(即: 广义表的头尾链表存储表示)来建立广义表的存储结构,则含有n个子表的广义表中有n个表结点序列。第i(i=1,2,…,n-1)个表结点中的表尾指针指向第i+1个表结点。第n个表节点的表尾指针为NULL,并且,如果把原子也看成是子表的话,则第i个节点的表头指针hp指向αi建立的子表(i=1,2,…,n)。由此,由S建广义表的问题可转化为由αi(i=1,2,…,n)建子表的问题。又,αi可能有3种情况:
1) 带括弧的空白串;
2) 长度为1的单字符串;
3) 长度>1的字符串;显然,前两种情况为递归的终结状态, 子表为空表或只含一个原子结点,后一种情况为递归调用。由此,在不考虑字符串可能出错的前提下,可得下列建立广义表链表存储结构的递归定义。
基本项: 置空广义表 当S为空表串时
建原子结点的子表 当S为单字符串时
归纳项: 假设sub为脱去S中最外层括弧的子串,记为's1,s2,...,sn',其中si(i=1,2,...n)为非空字符串。
对每一个si建立一个表节点,并令其hp域的指针为由si建立的子表的头指针,除最后建立的表结点的
尾指针为NULL外,其余表结点的尾指针均指向在它之后建立的表结点。
假定函数sever(str,hstr)的功能为: 从字符串str中取出第一个","之前的子串赋给hstr,并使str成为删去子串hstr和","之后的剩余串,若串str中没有字符",",则操作后的hstr即为操作前的str,而操作后的str为空串NULL。根据上述递归定义可得到建广义表存储结构的递归函数如算法5.7所示。函数sever如算法5.8所示。
算法5.7
Status CreateGList(GList &L, SString S)
{
//采用头尾链表存储结构,由广义表的书写形式串S创建广义表L。设emp="()"
if(StrCompare(S,emp)){
L = NULL; //创建空表
}
else{
if(!(L = (GList)malloc(sizeof(GLNode)))) //创建表节点
exit(OVERFLOW);
if(StrLength(S) == 1){ //创建单原子广义表
L->tag = ATOM;
L->atom = S;
}
else{
L->tag = LIST;
p = L;
SubString(sub, S, 2, StrLength(S) - 2); //脱外层括号
do{ //重复建n个子表
sever(sub, hsub); //sub中分离出表头串
CreateGList(p->ptr.hp, hsub);
q = p;
if(!StrEmpty(sub)){ //表尾不为空
if(!(p = (GLNode *)malloc(sizeof(GLNode))))
exit(OVERFLOW);
p->tag = LIST;
q->ptr.tp = p;
}
}while(!StrEmpty(sub));
q->ptr.tp = NULL;
}
}
return OK;
}算法5.8
Status sever(SString &str, SString &hstr)
{
//将非空串str分割成两部分: hstr为第一个','之前的子串,str为之后的子串
n = StrLength(str);
i = 0;
k = 0; //k记尚未配对的左括号个数
do{
++i;
SubString(ch, str, i, 1);
if(ch == '(')
++k;
else if(ch == ')')
--k;
}while(i < n && (ch != ',' || k != 0));
if(i < n){
SubString(hstr, str, 1, i-1);
SubString(str, str, i+1, n-i);
}else{
StrCopy(hstr, str);
ClearString(str);
}
return OK;
}注: SString结构0号单元存放串的长度。函数SubString(&sub, S, pos, len)用于将串从第pos个字符开始长度为len的字符序列复制到传Sub中。
[参看]:

