动态规划算法(转)
最近在牛客网上做了几套公司的真题,发现有关动态规划(Dynamic Programming)算法的题目很多。对于我来说,算法里面遇到的问题感觉最难的也就是动态规划(Dynamic Programming)算法了。于是花了好长时间,查找了相关的文献和资料准备彻底的理解动态规划(Dynamic Programming)算法。一是帮助自己总结知识点,二是也能够帮助他人更好的理解这个算法。后面的参考文献只是我看到的文献的一部分。
1. 动态规划算法的核心
理解一个算法就要理解一个算法的核心,动态规划算法的核心是下面的一张图片和一个小故事:
由上面的图片和小故事,可以知道动态规划算法的核心就是记住已经解决过的子问题的解。
2. 动态规划算法的两种形式
上面已经知道动态规划算法的核心就是记住已经求过的解,记住求解的方式有两种:
-
自顶向下的备忘录法
-
自底向上
为了说明动态规划的这两种方法,举一个最简单的例子: 求斐波那契数列Fibonacci。先看一下这个问题:
Fibonacci (n) = 0; n = 0
Fibonacci (n) = 1; n = 1
Fibonacci (n) = Fibonacci(n-1) + Fibonacci(n-2)以前学C语言的时候,我们使用递归的方法写过这个算法,十分简单。下面我们先来看一下递归的实现:
int fib(int n)
{
if (n <= 0)
return 0;
else if (n == 1)
return 1;
return fib(n-1) + fib(n-2);
}先来分析一下递归算法的执行流程,假如输入6,那么执行的递归树如下:
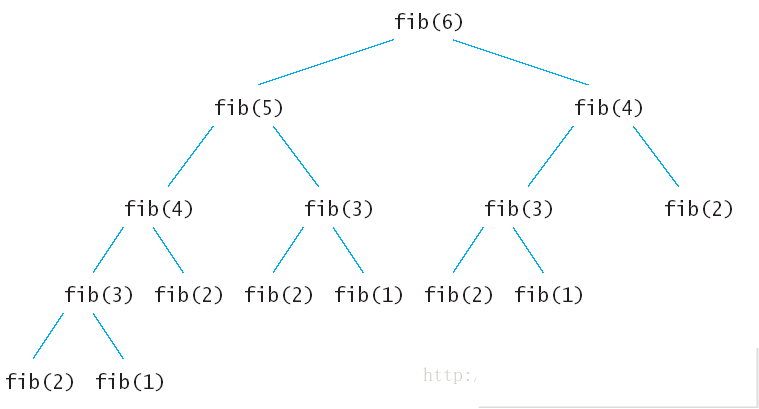
上面的递归树中每一个子节点都会执行一次,很多重复的节点被执行,其中fib(2)被重复执行了5次。由于调用每一个函数的时候都要保留上下文,所以空间上的开销也不小。这么多的子节点被重复执行,如果在执行的时候把执行过的子节点保存起来,后面要用到的时候直接查表调用的话,可以节约大量的时间。下面就看看动态规划的两种方法怎样来解决斐波那契数列Fibonacci数列问题。
2.1 自顶向下的备忘录法
int Fibonacci(int n)
{
if (n <= 0)
return 0;
int *mem = (int *)malloc(sizeof(int) * (n+1));
if(!mem)
return -1;
for(int i=0;i<=n;i++)
mem[i] = -1;
int sum = fib(n, mem);
free(mem);
return sum;
}
int fib(int n, int *mem)
{
if (n <= 0)
{
mem[0] = 0;
return 0;
}else if(n == 1){
mem[1] = 1;
return 1;
}else if (mem[n] != -1){
//如果已经求出了fib(n)的值直接返回,否则将求出的值保存在Memo备忘录中
return mem[n];
}
mem[n] = fib(n-1, mem) + fib(n-2, mem);
return mem[n];
}备忘录法也是比较好理解的,创建了一个n+1大小的数组来保存求出的斐波那契数列中的每一个值。在递归的时候如果发现前面fib(n)的值计算出来了就不再计算,如果未计算出来,则计算出来后保存在mem数组中,下次再调用fib(n)的时候就不会重新递归了。比如,上面的递归树中计算fib(6)的时候先计算fib(5),调用fib(5)算出了fib(4)后,fib(6)再调用fib(4)就不会再递归fib(4)的子树了,因为fib(4)的值已经保存在mem[4]中。
2.2 自底向上的的动态规划
备忘录法还是利用了递归,上面算法不管怎样,计算fib(6)的时候最后还要计算出fib(1)、fib(2)、fib(3)…,那么为何不先计算出fib(1)、fib(2)、fib(3)…呢?这也就是动态规划的核心,先计算子问题,再由子问题计算父问题。
int fib(int n)
{
if(n <= 0)
return 0;
int *mem = (int *)malloc(sizeof(int) * (n+1));
if(!mem)
return -1;
mem[0] = 0;
mem[1] = 1;
for(i = 2;i<=n;i++)
mem[i] = mem[i-1] + mem[i-2];
int sum = mem[n];
free(mem);
return sum;
}自底向上方法也是利用数组保存了先计算的值。观察参与循环的只有i、i-1、i-2三项,因此该方法的空间可以进一步压缩如下:
int fib(int n)
{
if(n <= 0)
return 0;
int a,b,c;
a = 0; b = 1; c = 1;
for(i = 2; i<=n;i++)
{
c = a + b;
a = b;
b = c;
}
return c;
}一般来说,由于备忘录方式的动态规划方法使用了递归,递归的时候会产生额外的开销,使用自底向上的动态规划方法要比备忘录方法好。
你以为看懂了上面的例子就懂了动态规划了吗?那就too young too simple了。动态规划远远不止如此简单,下面先给出一个例子看看能否独立完成。然后再对动态规划的其他特性进行分析。
3. 动态规划小试牛刀
下面的例子来自于算法导论:
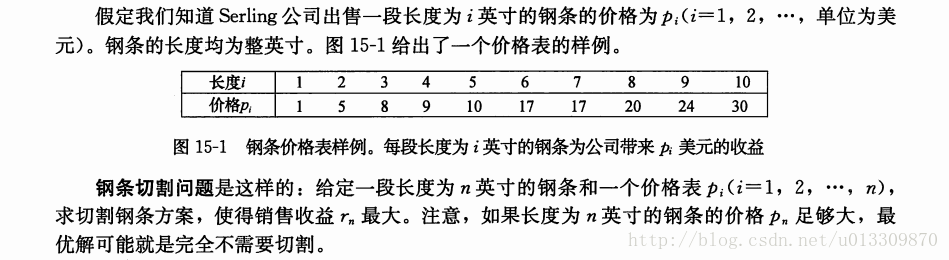
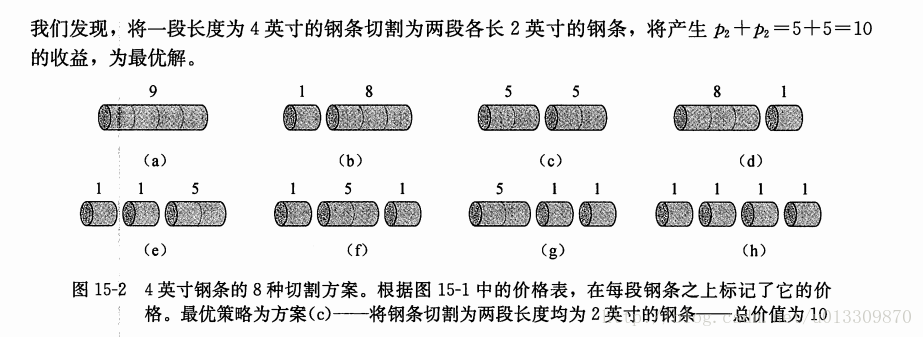


关于题目的讲解就直接截图算法导论书上了,这里就不展开讲。现在使用一下前面讲到的三种方法来实现一下。
3.1 朴素算法
最简单直接的想法,就是用暴力破解,n长的钢管,可以分解为i和n-i长的两段,因为i可以从0~n取值,所以我们可以对i不进行继续切割,于是对于长为i的这段,可以直接调用价钱数组p[i]来得到价钱,然后加上对n-i递归调用求最优收益的函数的返回值。在过程之中记录这些组合的最优收益,等循环结束的时候,就能得到最优的收益价钱。
假设r[n]代表的是n长的钢管的切割最佳收益值,数组p代表上面表中的价格,其中p[0]=0,从p[1]~p[10]对应上面表中的数据,那么按照上面的想法,有公式:
r[n] = max(p[i]+r[n-i]) 其中:i∈[1,n] 其中,i的取值范围为[1,n]。当n=0时,r[n]=0,因为0长度的钢管售价当然为0.
参看如下代码:
int cut_rod(int* p, int n)
{
if (n == 0) {
return 0;
}
int q = -1;
for (int i = 1; i <= n; i++) {
/*
* 将n长的钢条,分成i和n-i的两段,i长的那段不切割,而n-i的那段求最大
* 切割收益方式,然后相加;而q值是所有的组合中,最大收益的那个
*/
q = max(q, p[i] + cut_rod(p, n - i));
}
return q;
}这种方法比较容易理解,但是性能是不是好呢?可以简单的以n=4的情况来看一下:
n=4的划分(其中前面的那一段是直接使用p[i],后面一段调用函数来求最佳收益):
cut_rod(p,4)的划分可能: ①1长和3长:p[1]+cut_rod(p,3) ②2长和2长:p[2]+cut_rod(p,2) ③3长和1长:p[3]+cut_rod(p,1) ④4长和0长:p[4]+cut_rod(p,0)
而其中cut_rod(p,3)又可以划分为数组p中元素与cut_rod(p,0),cut_rod(p,1)和cut_rod(p,2);以此类推,可以给出一种以递归调用树的形式展示cut_rod递归调用了多少次:
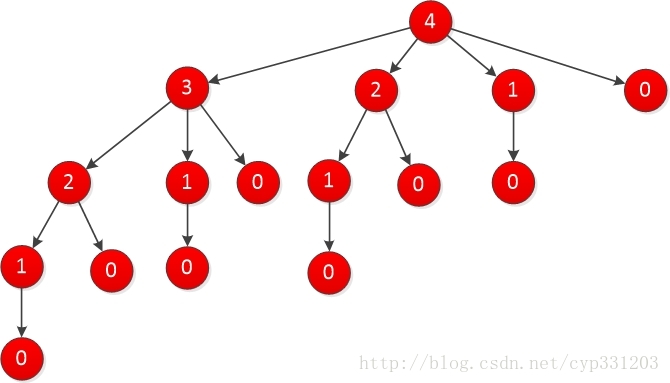
不难从图中看出,做了大量重复工作,以n=2的节点为例,分别在n=4和n=3的时候都被调用了。根据上图,可以给出递归调用次数的一个公式,假设T(n)表示cur_rod()第二个参数为n时的调用次数,T(0)这时候是为1的,因为根节点的第一次调用也要算进去。于是有:
T(n)=1+T(0)+T(1)+...+T(n-1)
使用归纳法,可以比较容易的得出:T(n)=2^n。 指数次幂的调用次数,显然太大,我们稍微让n大一点,则会让整个过程变的漫长。
3.2 动态规划算法
而实际上我们不需要在每次都去重新计算cut_rod的在n=2时的结果,只需要在第一次计算的时候将结果保存起来,然后再需要的时候直接使用即可。这其实就是所谓的动态规划算法。
这里的思路有两种,一种叫带备忘的自顶向下方法,是顺着之前的代码,当需要的时候去检查是不是已经计算好了,如果是,则直接使用,如果不是,则计算,并保存结果。第二种思路是自底向上方法,不论需不需要,先将子问题一一解决,然后再来解决更一级的问题,但要注意的是,我们需要先从最小的子问题开始,依次增加规模,这样每一次解决问题的时候,它的子问题都已经计算好了,直接使用即可。
1) 带备忘录的自顶向下方法
int memoized_cut_rod_aux(int* p, int n, int* r) {
if (r[n] >= 0) {
return r[n];
}
int q = -1;
if (n == 0) {
q = 0;
} else {
for (int i = 1; i <= n; i++) {
q = max(q, p[i] + memoized_cut_rod_aux(p, n - i, r));
}
}
r[n] = q;
return q;
}
/*
* 自顶向上的cut-rod的过程
*/
int memoized_cut_rod(int* p, int n) {
int* r = new int[n + 1];
//初始化r数组,r数组用来存放,某种解决方案的最大收益值,对于n长的钢条而言,有n+1种切割方案,所以数组n+1长
for (int i = 0; i <= n; i++) {
r[i] = -1;
}
return memoized_cut_rod_aux(p, n, r);
} 有了上面求斐波拉契数列的基础,理解备忘录方法也就不难了。备忘录方法无非是在递归的时候记录下已经调用过的子函数的值。这道钢条切割问题的经典之处在于自底向上的动态规划问题的处理,理解了这个也就理解了动态规划的精髓。
2) 自底向上的动态规划
/*
* 自底向上的方式,先计算更小的子问题,然后再算较大的子问题,由于较大的子问题依赖于更小的子问题的答案,所以在计算较
* 大的子问题的时候,就无需再去计算更小的子问题,因为那答案已经计算好,且存储起来了
*/
int bottom_up_cut_rod(int p[], int n)
{
int* r = new int[n + 1];
r[0] = 0; //将r[0]初始化为0,是因为0长的钢条没有收益
for (int j = 1; j <= n; j++) {
int q = -1;
/*
* 这里不用i=0开始,因为i=0开始不合适,因为这里总长就是为j,而划分是i和j-i的划分,如果i等于0,那么
* 就意味着要知道r[j-0]=r[j]的值也就是j长的最好划分的收益,但是我们这里不知道。而且对于p[0]而言本身就没有意义
* p数组中有意义的数据下标是从1到n的
*/
for (int i = 1; i <= j; i++)
{
q = max(q, p[i] + r[j - i]); //
}
r[j] = q;
}
return r[n];
} 上面两种算法的时间复杂度都是O(n^2)。
3) 重构解
上面的代码只给出了最优的收益值,但是却没有给出最优收益到底是在那种切割分配方式下得到的,比如说n=9时,最佳收益为25,要分成3和6两段。这里可以使用另一个数组s来存储分段情况,比如s[9]存储3,然后我们让n=9-3,就可以得到s[6]的最佳分段情况,发现就是6,于是就不需要继续。
只需要将代码稍微修改即可达到目的:
#include<iostream>
using namespace std;
/*
* 存储结果的结构体,里面包含r和s两个数组,分别保存最佳收益和最佳收益时的分段数值
*/
struct result {
int* r;
int* s;
int len;
result(int l): r(), s(), len(l) {
r = new int[len];
s = new int[len];
r[0] = 0;
}
~result() {
delete[] r;
delete[] s;
}
};
result* extended_bottom_up_cut_rod(int p[], int n)
{
result* res = new result(n + 1);
int q = -1;
//外层的循环代表的是保留的不切割的那段
for (int i = 1; i <= n; i++)
{
//内层的循环代表的是要分割的,且要求出最佳分割的那段
for (int j = 1; j <= i; j++)
{
if (q < p[j] + res->r[i - j])
{
q = p[j] + res->r[i - j];
res->s[i] = j;
}
}
res->r[i] = q;
}
return res;
}
int main(int argc, char *argv[]) {
int p[] = { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };
int n = 9;
result* res = extended_bottom_up_cut_rod(p, n);
cout << "最佳收益:" << res->r[9] << endl;
//循环输出实际的最佳分割段长
cout << "分段情况:";
while (n > 0)
{
cout << res->s[n] << ' ';
n = n - res->s[n];
}
delete res;
return 0;
} 运行上面程序,我们就可以的得到长度为9的钢管的最佳收益以及对应的切割情况:
最佳收益:25 分段情况:3 6
4. 动态规划原理
虽然已经用动态规划方法解决了上面两个问题,但是大家可能还跟我一样并不知道什么时候要用到动态规划。总结一下上面的斐波拉契数列和钢条切割问题,发现两个问题都涉及到了重叠子问题,和最优子结构。
①最优子结构
用动态规划求解最优化问题的第一步就是刻画最优解的结构,如果一个问题的解结构包含其子问题的最优解,就称此问题具有最优子结构性质。因此,某个问题是否适合应用动态规划算法,它是否具有最优子结构性质是一个很好的线索。使用动态规划算法时,用子问题的最优解来构造原问题的最优解。因此必须考查最优解中用到的所有子问题。
②重叠子问题
在斐波拉契数列和钢条切割结构图中,可以看到大量的重叠子问题,比如说在求fib(6)的时候,fib(2)被调用了5次,在求cut(4)的时候cut(0)被调用了4次。如果使用递归算法的时候会反复的求解相同的子问题,不停的调用函数,而不是生成新的子问题。如果递归算法反复求解相同的子问题,就称为具有重叠子问题(overlapping subproblems)性质。在动态规划算法中使用数组来保存子问题的解,这样子问题多次求解的时候可以直接查表不用调用函数递归。
5. 动态规划的经典模型
5.1 线性模型
线性模型的是动态规划中最常用的模型,上文讲到的钢条切割问题就是经典的线性模型,这里的线性指的是状态的排布是呈线性的。【例题1】是一个经典的面试题,我们将它作为线性模型的敲门砖。
【例题1】在一个夜黑风高的晚上,有n(n <= 50)个小朋友在桥的这边,现在他们需要过桥,但是由于桥很窄,每次只允许不大于两人通过,他们只有一个手电筒,所以每次过桥的两个人需要把手电筒带回来,i号小朋友过桥的时间为T[i],两个人过桥的总时间为二者中时间长者。问所有小朋友过桥的总时间最短是多少。

每次过桥的时候最多两个人,如果桥这边还有人,那么还得回来一个人(送手电筒),也就是说N个人过桥的次数为2*N-3(倒推,当桥这边只剩两个人时只需要一次,三个人的情况为来回一次后加上两个人的情况…)。有一个人需要来回跑,将手电筒送回来(也许不是同一个人,realy?!)这个回来的时间是没办法省去的,并且回来的次数也是确定的,为N-2,如果是我,我会选择让跑的最快的人来干这件事情,但是我错了…如果总是跑得最快的人跑回来的话,那么他在每次别人过桥的时候一定得跟过去,于是就变成就是很简单的问题了,花费的总时间:
T = minPTime * (N-2) + (totalSum-minPTime)
来看一组数据 四个人过桥花费的时间分别为 1 2 5 10,按照上面的公式答案是19,但是实际答案应该是17。
具体步骤是这样的:
第一步:1和2过去,花费时间2,然后1回来(花费时间1); 第二歩:3和4过去,花费时间10,然后2回来(花费时间2); 第三部:1和2过去,花费时间2,总耗时17。
所以之前的贪心想法是不对的。我们先将所有人按花费时间递增进行排序,假设前i个人过河花费的最少时间为opt[i],那么考虑前i-1个人过河的情况,即河这边还有1个人,河那边有i-1个人,并且这时候手电筒肯定在对岸,所以opt[i] = opt[i-1] + a[1] + a[i] (让花费时间最少的人把手电筒送过来,然后和第i个人一起过河)。如果河这边还有两个人,一个是第i号,另外一个无所谓,河那边有i-2个人,并且手电筒肯定在对岸,所以opt[i] = opt[i-2] + a[1] + a[i] + 2*a[2] (让花费时间最少的人把电筒送过来,然后第i个人和另外一个人一起过河,由于花费时间最少的人在这边,所以下一次送手电筒过来的一定是花费次少的,送过来后花费最少的和花费次少的一起过河,解决问题)
所以 opt[i] = min{opt[i-1] + a[1] + a[i] , opt[i-2] + a[1] + a[i] + 2*a[2] }
5.2 区间模型
区间模型的状态表示一般为d[i][j],表示区间[i, j]上的最优解,然后通过状态转移计算出[i+1, j]或者[i, j+1]上的最优解,逐步扩大区间的范围,最终求得[1, len]的最优解。
【例题2】给定一个长度为n(n <= 1000)的字符串A,求插入最少多少个字符使得它变成一个回文串。
典型的区间模型,回文串拥有很明显的子结构特征,即当字符串X是一个回文串时,在X两边各添加一个字符’a’后,aXa仍然是一个回文串,我们用d[i][j]来表示A[i…j]这个子串变成回文串所需要添加的最少的字符数,那么对于A[i] == A[j]的情况,很明显有 d[i][j] = d[i+1][j-1] (这里需要明确一点,当i+1 > j-1时也是有意义的,它代表的是空串,空串也是一个回文串,所以这种情况下d[i+1][j-1] = 0);当A[i] != A[j]时,我们将它变成更小的子问题求解,我们有两种决策:
1、在A[j]后面添加一个字符A[i];
2、在A[i]前面添加一个字符A[j];
根据两种决策列出状态转移方程为:
d[i][j] = min{ d[i+1][j], d[i][j-1] } + 1; (每次状态转移,区间长度增加1)
空间复杂度O(n^2),时间复杂度O(n^2), 下文会提到将空间复杂度降为O(n)的优化算法。
5.3 背包模型
背包问题是动态规划中一个最典型的问题之一。由于网上有非常详尽的背包讲解,这里只将常用部分抽出来。
【例题3】有N种物品(每种物品1件)和一个容量为V的背包。放入第 i 种物品耗费的空间是Ci,得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。决策为第i个物品在前i-1个物品放置完毕后,是选择放还是不放,状态转移方程为:
f[i][v] = max{ f[i-1][v], f[i-1][v – Ci] +Wi }
时间复杂度O(VN),空间复杂度O(VN) (空间复杂度可利用滚动数组进行优化达到O(V))。
6. 动态规划题集整理
1) 最长单调子序列
Constructing Roads In JG Kingdom★★☆☆☆
Stock Exchange ★★☆☆☆
2) 最大M子段和
Max Sum ★☆☆☆☆
最长公共子串 ★★☆☆☆
3) 线性模型
Skiing ★☆☆☆☆
[参看]:

