core/ngx_crc.h源文件分析

这里我们主要讲述一下crc(循环冗余校验），再接着讲述一下ngx_crc()这一nginx内部的实现。

1. 循环冗余校验(crc)

Cyclic Redundancy Check循环冗余校验，是基于数据计算一组校验码，用于核对数据传输过程中是否被更改或者传输错误。

1.1 算法原理

假设数据传输过程中需要发送15位的二进制信息g=101001110100001，这串二进制码可表示为代数多项式g(x) = x^14 + x^12 + x^9 + x^8 + x^7 + x^5 + 1，其中g中第k位的值，对应g(x)中x^k的系数。将g(x)乘以x^m，既将g后加m个0，然后除以m阶多项式h(x)，得到的(m-1)阶余项r(x)对应的二进制码r就是CRC编码。

h(x)可以自由选择或者使用国际通行标准，一般按照h(x)的阶数m，将CRC算法称为CRC-m，比如CRC-32、CRC-64等。国际通行标准可以参看http://en.wikipedia.org/wiki/Cyclic_redundancy_check

g(x)和h(x)的除运算，可以通过g和h做xor（异或）运算。比如将11001与10101做xor运算:

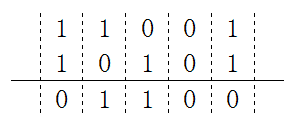
ngx-crc001

明白了xor运算法则后，举一个例子使用CRC-8算法求101001110100001的效验码。CRC-8标准的h(x) = x^8 + x^7 + x^6 + x^4 + x^2 + 1，既h是9位的二进制串111010101。

ngx-crc002

经过迭代运算后，最终得到的r是10001100，这就是CRC效验码。

1.2 crc直接移位算法

通过示例，可以发现一些规律，依据这些规律调整算法：

1) 每次迭代，根据gk的首位决定b，b是与gk进行运算的二进制码。若gk的首位是1，则b=h；若gk的首位是0，则b=0，或者跳过此次迭代，上面的例子中就是碰到0后直接跳到后面的非零位。

ngx-crc003

2) 每次迭代，gk的首位将会被移出，所以只需考虑第2位后计算即可。这样就可以舍弃h的首位，将b取h的后m位。比如CRC-8的h是111010101，b只需是11010101。

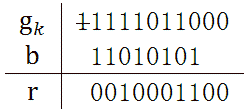
ngx-crc004

3) 每次迭代，受到影响的是gk的前m位，所以构建一个m位的寄存器S，此寄存器储存gk的前m位。每次迭代计算前先将S的首位抛弃，将寄存器左移一位，同时将g的后一位加入寄存器。若使用此种方法，计算步骤如下：

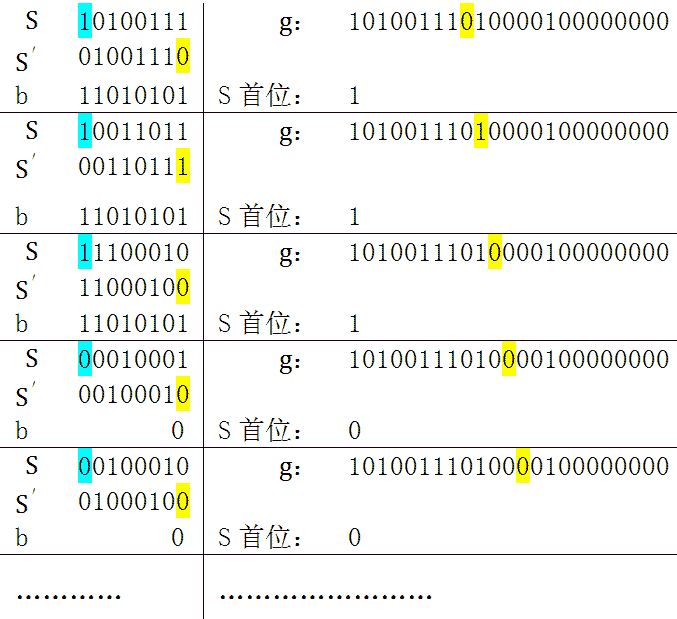
ngx-crc005

※蓝色表示寄存器S的首位，是需要移出的，b根据S的首位选择0或者h。黄色是需要移入寄存器的位。S’是经过位移后的S。

如上原理图解，直接的crc-32校验代码如下：

unsigned direct_crc32(char *buf,size_t bufsz)
{
   unsigned int crc32;
   int i;
   crc32 = CRC_Init;

   while(bufsz--)
   {
        crc32 = (crc32 >> 8)^(*buf++);   //这里注意应该把上一次结果的低字节位移出
        for(i = 0;i<8;i++)
        {
             if(crc32 & 0x1)
             {
                crc32 >>= 1;         //将低位移出
                crc32 ^= CRC_POLY;
             }
             else{
                crc32 >>= 1;
             }
        }
   }

   crc32 ^= CRC_Init;

   return crc32;
}

1.2 查表法

同样是上面的那个例子，将数据按每4位组成1个block，这样g就被分成6个block。

ngx-crc006

下面的表展示了4次迭代计算步骤，灰色背景的位是保存在寄存器中的。

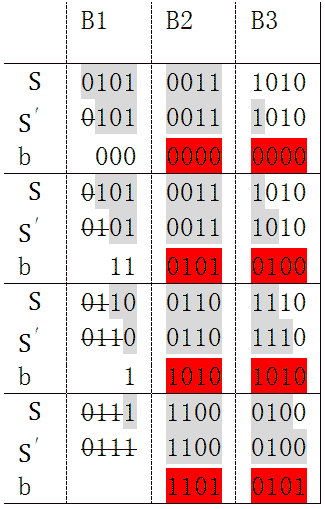
ngx-crc007

经4次迭代，B1被移出寄存器。被移出的部分，不我们关心的，我们关心的是这4次迭代对B2和B3产生了什么影响。注意表中红色的部分，先作如下定义：

   B23 = 00111010
   b1 = 00000000
   b2 = 01010100
   b3 = 10101010
   b4 = 11010101
   b' = b1 xor b2 xor b3 xor b4

4次迭代对B2和B3来说,实际上就是让它们与b1,b2,b3,b4做了xor计算，既：

   B23 xor b1 xor b2 xor b3 xor b4

可以证明xor运算满足交换律和结合律，于是：

   B23 xor b1 xor b2 xor b3 xor b4 = B23 xor (b1 xor b2 xor b3 xor b4) = B23 xor b'

b1是由B1的第1位决定的，b2是由B1迭代1次后的第2位决定（既是由B1的第1和第2位决定），同理,b3和b4都是由B1决定。通过B1就可以计算出b'。另外，B1由4位组成，其一共2^4有种可能值。于是我们就可以想到一种更快捷的算法，事先将b'所有可能的值，16个值可以看成一个表；这样就可以不必进行那4次迭代，而是用B1查表得到b'值，将B1移出，B3移入，与b'计算，然后是下一次迭代。

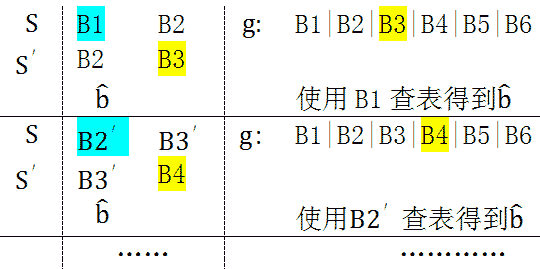
ngx-crc008

可看到每次迭代，寄存器中的数据以4位为单位移入和移出，关键是通过寄存器前4位查表获得，这样的算法可以大大提高运算速度。

上面的方法是半字节查表法，另外还有单字节和双字节查表法，原理都是一样的——事先计算出2^8或2^16个b'的可能值，迭代中使用寄存器前8位或16位查表获得b'。

1.4 示例

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdint.h>

uint32_t  ngx_crc32_table256[] = {
    0x00000000, 0x77073096, 0xee0e612c, 0x990951ba,
    0x076dc419, 0x706af48f, 0xe963a535, 0x9e6495a3,
    0x0edb8832, 0x79dcb8a4, 0xe0d5e91e, 0x97d2d988,
    0x09b64c2b, 0x7eb17cbd, 0xe7b82d07, 0x90bf1d91,
    0x1db71064, 0x6ab020f2, 0xf3b97148, 0x84be41de,
    0x1adad47d, 0x6ddde4eb, 0xf4d4b551, 0x83d385c7,
    0x136c9856, 0x646ba8c0, 0xfd62f97a, 0x8a65c9ec,
    0x14015c4f, 0x63066cd9, 0xfa0f3d63, 0x8d080df5,
    0x3b6e20c8, 0x4c69105e, 0xd56041e4, 0xa2677172,
    0x3c03e4d1, 0x4b04d447, 0xd20d85fd, 0xa50ab56b,
    0x35b5a8fa, 0x42b2986c, 0xdbbbc9d6, 0xacbcf940,
    0x32d86ce3, 0x45df5c75, 0xdcd60dcf, 0xabd13d59,
    0x26d930ac, 0x51de003a, 0xc8d75180, 0xbfd06116,
    0x21b4f4b5, 0x56b3c423, 0xcfba9599, 0xb8bda50f,
    0x2802b89e, 0x5f058808, 0xc60cd9b2, 0xb10be924,
    0x2f6f7c87, 0x58684c11, 0xc1611dab, 0xb6662d3d,
    0x76dc4190, 0x01db7106, 0x98d220bc, 0xefd5102a,
    0x71b18589, 0x06b6b51f, 0x9fbfe4a5, 0xe8b8d433,
    0x7807c9a2, 0x0f00f934, 0x9609a88e, 0xe10e9818,
    0x7f6a0dbb, 0x086d3d2d, 0x91646c97, 0xe6635c01,
    0x6b6b51f4, 0x1c6c6162, 0x856530d8, 0xf262004e,
    0x6c0695ed, 0x1b01a57b, 0x8208f4c1, 0xf50fc457,
    0x65b0d9c6, 0x12b7e950, 0x8bbeb8ea, 0xfcb9887c,
    0x62dd1ddf, 0x15da2d49, 0x8cd37cf3, 0xfbd44c65,
    0x4db26158, 0x3ab551ce, 0xa3bc0074, 0xd4bb30e2,
    0x4adfa541, 0x3dd895d7, 0xa4d1c46d, 0xd3d6f4fb,
    0x4369e96a, 0x346ed9fc, 0xad678846, 0xda60b8d0,
    0x44042d73, 0x33031de5, 0xaa0a4c5f, 0xdd0d7cc9,
    0x5005713c, 0x270241aa, 0xbe0b1010, 0xc90c2086,
    0x5768b525, 0x206f85b3, 0xb966d409, 0xce61e49f,
    0x5edef90e, 0x29d9c998, 0xb0d09822, 0xc7d7a8b4,
    0x59b33d17, 0x2eb40d81, 0xb7bd5c3b, 0xc0ba6cad,
    0xedb88320, 0x9abfb3b6, 0x03b6e20c, 0x74b1d29a,
    0xead54739, 0x9dd277af, 0x04db2615, 0x73dc1683,
    0xe3630b12, 0x94643b84, 0x0d6d6a3e, 0x7a6a5aa8,
    0xe40ecf0b, 0x9309ff9d, 0x0a00ae27, 0x7d079eb1,
    0xf00f9344, 0x8708a3d2, 0x1e01f268, 0x6906c2fe,
    0xf762575d, 0x806567cb, 0x196c3671, 0x6e6b06e7,
    0xfed41b76, 0x89d32be0, 0x10da7a5a, 0x67dd4acc,
    0xf9b9df6f, 0x8ebeeff9, 0x17b7be43, 0x60b08ed5,
    0xd6d6a3e8, 0xa1d1937e, 0x38d8c2c4, 0x4fdff252,
    0xd1bb67f1, 0xa6bc5767, 0x3fb506dd, 0x48b2364b,
    0xd80d2bda, 0xaf0a1b4c, 0x36034af6, 0x41047a60,
    0xdf60efc3, 0xa867df55, 0x316e8eef, 0x4669be79,
    0xcb61b38c, 0xbc66831a, 0x256fd2a0, 0x5268e236,
    0xcc0c7795, 0xbb0b4703, 0x220216b9, 0x5505262f,
    0xc5ba3bbe, 0xb2bd0b28, 0x2bb45a92, 0x5cb36a04,
    0xc2d7ffa7, 0xb5d0cf31, 0x2cd99e8b, 0x5bdeae1d,
    0x9b64c2b0, 0xec63f226, 0x756aa39c, 0x026d930a,
    0x9c0906a9, 0xeb0e363f, 0x72076785, 0x05005713,
    0x95bf4a82, 0xe2b87a14, 0x7bb12bae, 0x0cb61b38,
    0x92d28e9b, 0xe5d5be0d, 0x7cdcefb7, 0x0bdbdf21,
    0x86d3d2d4, 0xf1d4e242, 0x68ddb3f8, 0x1fda836e,
    0x81be16cd, 0xf6b9265b, 0x6fb077e1, 0x18b74777,
    0x88085ae6, 0xff0f6a70, 0x66063bca, 0x11010b5c,
    0x8f659eff, 0xf862ae69, 0x616bffd3, 0x166ccf45,
    0xa00ae278, 0xd70dd2ee, 0x4e048354, 0x3903b3c2,
    0xa7672661, 0xd06016f7, 0x4969474d, 0x3e6e77db,
    0xaed16a4a, 0xd9d65adc, 0x40df0b66, 0x37d83bf0,
    0xa9bcae53, 0xdebb9ec5, 0x47b2cf7f, 0x30b5ffe9,
    0xbdbdf21c, 0xcabac28a, 0x53b39330, 0x24b4a3a6,
    0xbad03605, 0xcdd70693, 0x54de5729, 0x23d967bf,
    0xb3667a2e, 0xc4614ab8, 0x5d681b02, 0x2a6f2b94,
    0xb40bbe37, 0xc30c8ea1, 0x5a05df1b, 0x2d02ef8d
};


static uint32_t
ngx_crc32_long(unsigned char  *p, size_t len)
{
    uint32_t  crc;

    crc = 0xffffffff;

    while (len--) {
        crc = ngx_crc32_table256[(crc ^ *p++) & 0xff] ^ (crc >> 8);
    }

    return crc ^ 0xffffffff;
}

#define CRC_POLY 0xEDB88320
unsigned direct_crc32(char *buf,size_t bufsz)
{
   unsigned int crc32;
   int i;
   crc32 = 0xFFFFFFFF;

   while(bufsz--)
   {
       crc32 ^= *buf++;
	   for(i = 0;i<8;i++)
	   {
	   		if(crc32 & 0x1)
			{
				crc32 >>= 1;
				crc32 ^= CRC_POLY;
			}
			else{
				crc32 >>= 1;
			}
		}
   }

   crc32 ^= 0xFFFFFFFF;

   return crc32;
}


int main(int argc,char *argv[])
{
    char buf[]="abcdefghijklmnopqrstuvwxyz";
	size_t len = sizeof(buf) - 1;

	unsigned int crc1,crc2;

	crc1 = ngx_crc32_long(buf,len);
	crc2 = direct_crc32(buf,len);

	printf("crc1: 0x%08X\n",crc1);
	printf("crc2: 0x%08X\n",crc2);

	return 0x0;
}

编译运行：

# gcc -o test_crc test_crc.c
# ./test_crc 
crc1: 0x4C2750BD
crc2: 0x4C2750BD

1.5 反向算法

之前讨论的算法可以称为正向CRC算法，意思是将g左边的位看作是高位，右边的位看作低位。G的右边加m个0，然后迭代计算是从高位开始，逐步将低位加入到寄存器中。在实际的数据传送过程中，是一边接收数据，一边计算CRC码，正向算法将新接收的数据看作低位。

逆向算法顾名思义就是将左边的数据看作低位，右边的数据看作高位。这样的话需要在g的左边加m个0，h也要逆向，例如正向CRC-16算法h=0x4c11db8，逆向CRC-16算法h=0xedb88320。b的选择0还是h，由寄存器中右边第1位决定，而不是左边第1位。寄存器仍旧是向左位移，就是说迭代变成从低位到高位。

ngx-crc009

2. core/ngx_crc.h头文件

/*
 * Copyright (C) Igor Sysoev
 * Copyright (C) Nginx, Inc.
 */


#ifndef _NGX_CRC_H_INCLUDED_
#define _NGX_CRC_H_INCLUDED_


#include <ngx_config.h>
#include <ngx_core.h>


/* 32-bit crc16 */

static ngx_inline uint32_t
ngx_crc(u_char *data, size_t len)
{
    uint32_t  sum;

    for (sum = 0; len; len--) {

        /*
         * gcc 2.95.2 x86 and icc 7.1.006 compile
         * that operator into the single "rol" opcode,
         * msvc 6.0sp2 compiles it into four opcodes.
         */
        sum = sum >> 1 | sum << 31;

        sum += *data++;
    }

    return sum;
}


#endif /* _NGX_CRC_H_INCLUDED_ */

这里函数ngx_crc()并不是一个标准的crc校验算法。

[参考]:

Ivanzz

发上等愿，结中等缘，享下等福；择高处立，寻平处住，向宽处行