AVL树原理及实现

本文主要讲述一下AVL树的原理及实现。

1. AVL树定义

在计算机科学中，AVL树是最先发明的自平衡二叉查找树。对于一般的搜索二叉树而言，如果数据恰好是按照从小到大（或从大到小）的顺序插入的，那么搜索二叉树就退化为链表，这个时候插入和删除的时间都会上升到O(n)，而对于海量数据而言是无法忍受的。即使是一棵由完全随机的数据构造成的搜索二叉树，从统计角度去分析，在进行若干次插入和删除操作，这棵搜索二叉树的高度也不能令人满意。这个时候大家就希望能有一种二叉树解决上述问题。平衡搜索二叉树，它的基本原理就是在插入和删除的时候，根据情况进行调整，以降低二叉树的高度。平衡搜索二叉树的代表就是AVL树和红黑树。

1） AVL树的定义

AVL树中任何节点的两棵子树的高度之差的绝对值不超过1，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(logn)。增加和删除可能需要通过一次或多次树旋转来重新平衡这棵树。AVL树得名于它的发明者G.M. Adelson-Velsky 和 E.M. Landis，他们在1962年论文”An algorithm for the organization of information”中发表了它。

注： AVL树定义并不是说从根节点到叶子节点的最长距离比最短距离大1

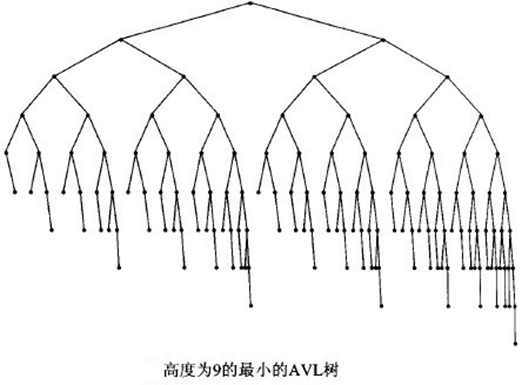
ds-avl-tree

上图就是一棵AVL树，从根节点到叶子节点的最短距离是5，最长距离是9.

2) AVL树的特点

本身首先是一棵二叉搜索树
带有平衡条件：每个节点的左右子树的高度之差的绝对值（平衡因子）最多为1。

注： 节点的平衡因子是它的左子树的高度减去右子树的高度。带有平衡因子1、0或-1的节点被认为是平衡的。

2. 旋转的定义

因为很多书中对旋转的定义不一致，所以我们有必要在这里说明一下：

以某一节点为轴，它的左枝顺时针旋转，作为新子树的根，我们称之为顺时针旋转（clockwise)或者右旋转；

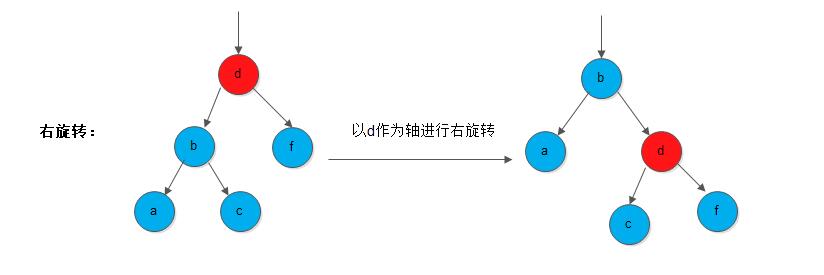
ds-node-right-rotate

下面给出右旋转伪代码：

struct AVLNode *right_rotate(struct AVLNode *node)
{
    struct AVLNode *left = node->left;
    node->left = left->right;
    left->right = node;

    return left;
}

以某一节点为轴，它的右枝逆时针旋转，作为新子树的根，我们称为逆时钟旋转(anti clockwise)或者左旋转;

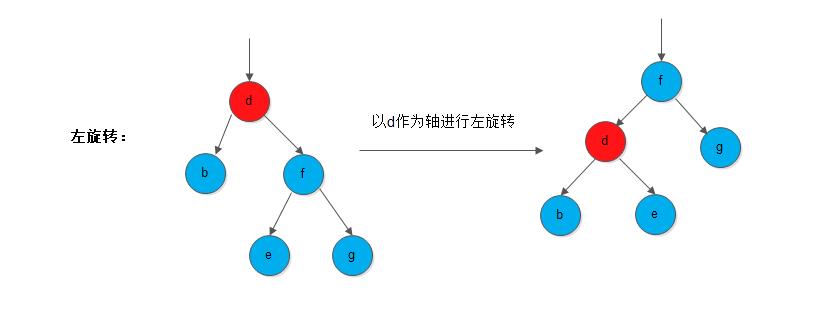
ds-node-left-rotate

下面给出左旋转伪代码：

struct AVLNode *left_rotate(struct AVLNode *node)
{
    struct AVLNode *right = node->right;
    node->right = right->left;
    right->left = node;

    return right;
}

说明：对于上面的右旋转、左旋转, 都不会影响到旋转节点的父节点。

3. AVL树的插入操作

AVL树的插入操作首先会按照普通搜索二叉树的插入操作进行，当插入一个数据后，我们会沿着插入数据时所经过的节点回溯。回溯的过程中会判断回溯路径中每个节点的左子树高度与右子树高度之差的绝对值是否超过1，如果超过1我们进行调整，调整的目的是使得该节点满足AVL树的定义。调整的情况可以分为以下四种旋转操作，旋转操作可以降低树的高度，同时不改变搜索二叉树的性质（即任何一个节点左子树中节点的key小于该节点的key，右子树中节点的key大于该节点的key)。

1) 情形1

节点X左子树比右子树高度大2，且插入节点位于X左孩子节点XL左子树上：

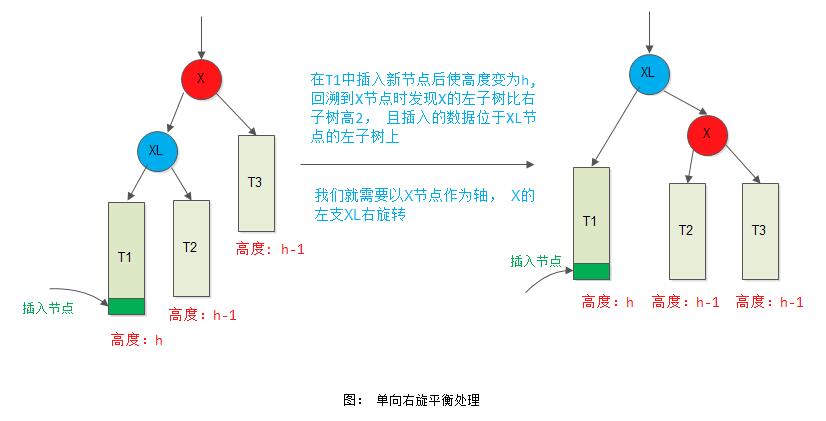
ds-avl-right-rotate

2) 情形2

节点X的右子树比左子树高度大2，且插入节点位于X右孩子节点XR的右子树上。

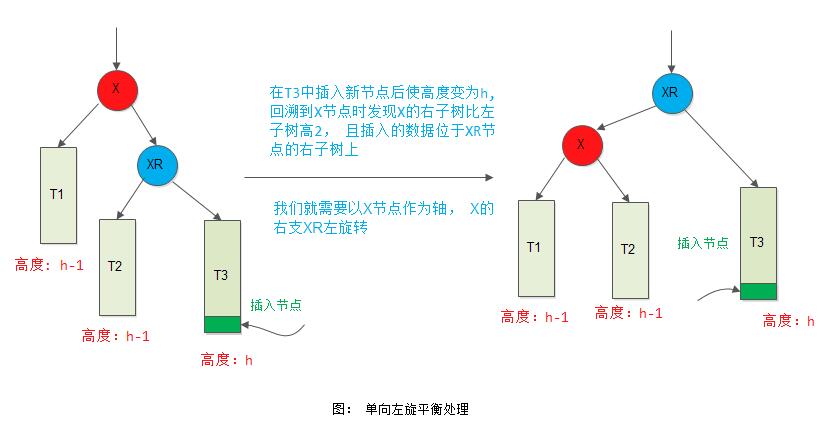
ds-avl-left-rotate

3) 情形3

节点X左子树比右子树高度大2，且插入节点位于X左孩子XL的右子树上：

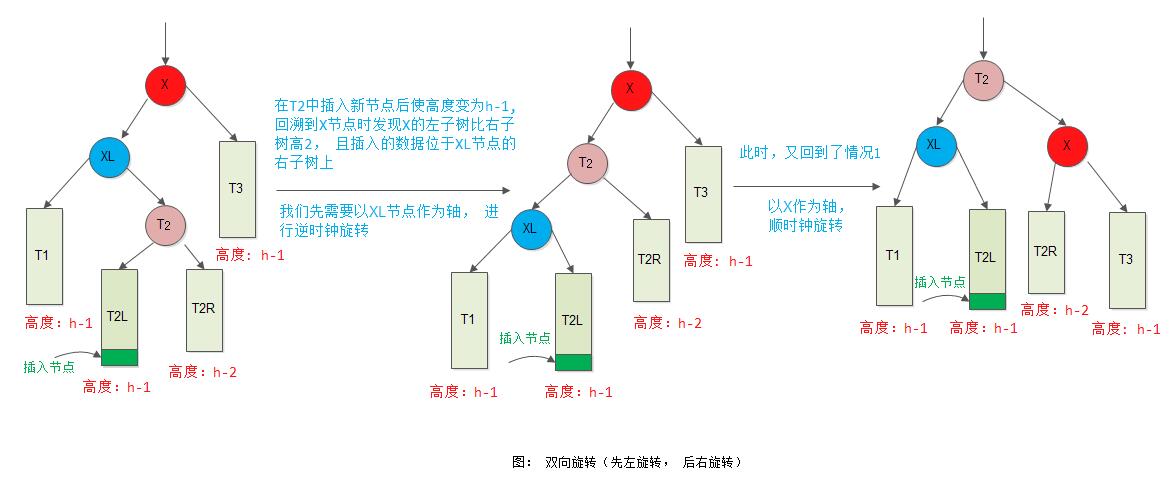
ds-avl-left-right-rotate

4) 情形4

节点X的右子树比左子树高度大2，且插入节点位于X右孩子XR的左子树上：

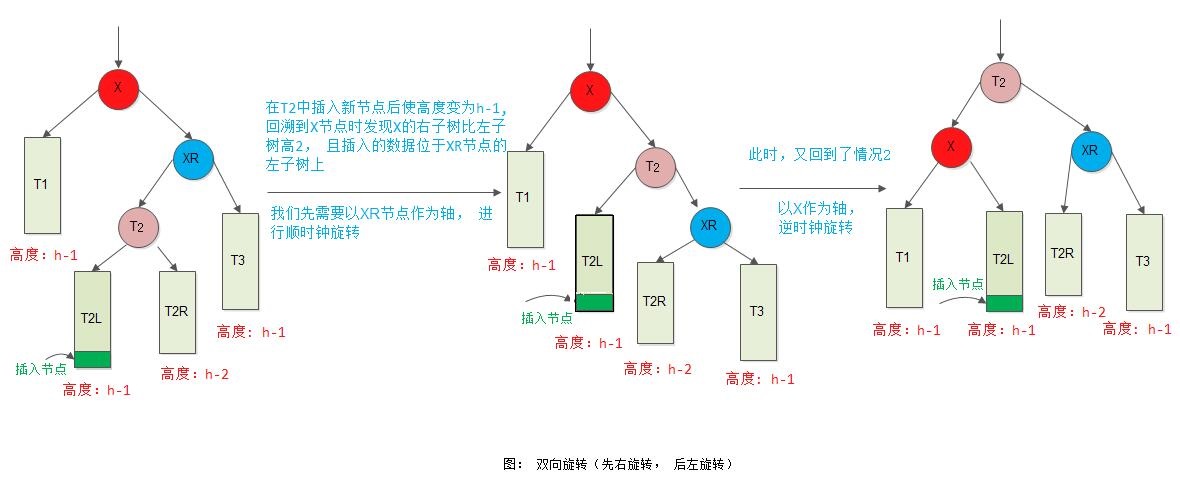
ds-avl-right-left-rotate

4. AVL树的删除操作

AVL树的删除操作和插入操作一样，首先会按照普通搜索二叉树的删除操作进行。当删除一个数据后，和插入操作一样，我们通常采取的策略是沿着删除数据时所经过的节点回溯，回溯的过程中会判断该节点的左右子树的高度之差是否超过1，如果超过1，我们就进行调整，调整的目的是使得该节点满足AVL树的定义。调整情况可以分为4种，和插入过程完全一样，这里不再赘述。

5. 相关源代码实现

5.1 avltree.h头文件

头文件avltree.h:

#ifndef __AVLTREE_H_
#define __AVLTREE_H_



typedef struct Node{
	int height;       //the height of the branch
	int data;
	struct Node *left;
	struct Node *right;
}AVLNode, *AVLTree;


int insert_node(AVLTree *root, int data);

int remove_node(AVLTree *root, int data);

int find(AVLTree root, int data);

int destroy(AVLTree *root);

// just for test

void inorder_traverse(AVLTree root);

void preorder_traverse(AVLTree root);

void postorder_traverse(AVLTree root);


#endif

5.2 avltree.c源代码文件

源文件avltree.c:

#include <stdio.h>
#include <stdlib.h>
#include "avltree.h"


#define MAX(x1, x2) ((x1) > (x2) ? (x1) : (x2))


//some helper functions
static int getheight(AVLTree node);

static void left_rotate(AVLTree *node);

static void right_rotate(AVLTree *node);

static int findmin(AVLTree node);



// the height of the empty tree is 0
static int getheight(AVLTree node)
{
	if(!node)
		return 0;

	return node->height;
}

static void left_rotate(AVLTree *node)
{
	AVLNode *p = *node;
	AVLNode *r = p->right;

	p->right = r->left;
	r->left = p;
	*node = r;

	//change the node's height
	p->height = MAX(getheight(p->left), getheight(p->right)) + 1;

	r->height = MAX(getheight(r->left), getheight(r->right)) + 1;
}


static void right_rotate(AVLTree *node)
{
	AVLNode *p = *node;
	AVLNode *lnode = p->left;

	p->left = lnode->right;
	lnode->right = p;
	*node = lnode;

	//change the node's height
	p->height = MAX(getheight(p->left), getheight(p->right)) + 1;

	lnode->height = MAX(getheight(lnode->left), getheight(lnode->right)) + 1;
}


static int findmin(AVLTree node)
{
	if(node == NULL)
		return -1;

	while(node->left)
		node = node->left;

	return node->data;
}


/*
 * insert data into avltree
 *
 * return: 0--success    -1--failure
 */
int insert_node(AVLTree *root, int data)
{
	if(!*root)
	{
		*root = (AVLNode *)malloc(sizeof(AVLNode));
		if(!*root)
			return -1;
		(*root)->data = data;
		(*root)->height = 1;
		(*root)->left = (*root)->right = NULL;
		return 0x0;
	}

	if((*root)->data == data)
		return -1;
	else if((*root)->data < data)
	{
		//insert in right tree
		if(insert_node(&(*root)->right,data) < 0)
			return -1;

		int lchild_height = getheight((*root)->left);
		int rchild_height = getheight((*root)->right);

		//after insert, we should check whether it is balanced
		//Here because we insert at the right branch, so rchild_height >= lchild_height
		if(rchild_height - lchild_height == 2)
		{
			if((*root)->right->data < data)
			{
				//Please reference 'AVLTree insert' chapter , this is the case 2
				left_rotate(root);
			}
			else{
				//Please reference 'AVLTree insert' chapter, this is the case 4
				right_rotate(&(*root)->right);
				left_rotate(root);
			}
		}

	}
	else{
		//insert in left tree
		if(insert_node(&(*root)->left, data) < 0)
			return -1;

		int lchild_height = getheight((*root)->left);
		int rchild_height = getheight((*root)->right);

		//after insert, we should check whether it is balanced
		//Here because we insert at the left branch, so lchild_height >= rchild_height
		if(lchild_height - rchild_height == 2)
		{
			if((*root)->left->data > data)
			{
				//Please reference 'AVLTree insert' chapter, this is the case 1
				right_rotate(root);
			}
			else{
				//Please reference 'AVLTree insert' chapter, this is the case 3
				left_rotate(&(*root)->left);
				right_rotate(root);
			}
		}

	}

	//update the current node height(这里其实是计算ABS(lchild_height - rchild_height) != 2时高度的变化，
	//等于2时的情况其实在旋转时就已经计算过了）
	(*root)->height = MAX(getheight((*root)->left), getheight((*root)->right)) + 1;
	return 0x0;
}


/*
 * remove data from avltree
 */
int remove_node(AVLTree *root, int data)
{
	if(*root == NULL)
	{
		// the tree is empty or the avltree doesn't have a node which data equals 'data'
		return -1;
	}

	//find the node
	if((*root)->data == data)
	{

		if((*root)->left != NULL && (*root)->right != NULL)
		{
			// the left child and the right child is not null, we find the 'next' node
			int key = findmin((*root)->right);
			(*root)->data = key;

			//remove the 'next' node, and it will must successful
			remove_node(&(*root)->right, key);

			int lchild_height = getheight((*root)->left);
			int rchild_height = getheight((*root)->right);


			//Bacause here we remove the node at right-branch, so lchild_height >= rchild_height
			if(lchild_height - rchild_height == 2)
			{
				//Note: when remove, here is '>='
				if(getheight((*root)->left->left) >= getheight((*root)->left->right))
				{
					//Please reference 'AVLTree insert' chapter, this is the case 1
					right_rotate(root);
				}
				else{
					//Please reference 'AVLTree insert' chapter, this is the case 3
					left_rotate(&(*root)->left);
					right_rotate(root);
				}
			}

		}
		else if((*root)->left == NULL)
		{
			//Here the left branch is NULL
			AVLNode *node = *root;
			*root = node->right;
			free(node);
			node = NULL;
			return 0x0;
		}
		else{
			//Here the right branch is NULL
			AVLNode *node = *root;
			*root = node->left;
			free(node);
			node = NULL;
			return 0x0;
		}
	}
	else if((*root)->data < data)
	{
		//find the node at the right-branch
		if(remove_node(&(*root)->right, data) < 0)
			return -1;

		int lchild_height = getheight((*root)->left);
		int rchild_height = getheight((*root)->right);

		//Because we remove the node at the right-branch, so lchild_height >= rchild_height
		if(lchild_height - rchild_height == 2)
		{
			//Note: when remove, here is '>='
			if(getheight((*root)->left->left) >= getheight((*root)->left->right))
			{
				//Please reference 'AVLTree insert' chapter, this is the case 1
				right_rotate(root);
			}
			else{
				//Please reference 'AVLTree insert' chapter, this is the case 3
				left_rotate(&(*root)->left);
				right_rotate(root);
			}
		}
	}
	else{
		//find the node at the left-branch
		if(remove_node(&(*root)->left, data) < 0)
			return -1;

		int lchild_height = getheight((*root)->left);
		int rchild_height = getheight((*root)->right);

		//Because we remove the node at the left-branch, so rchild_height >= lchild_height
		if(rchild_height - lchild_height == 2)
		{
			//Note: when remove, there is '>='
			if(getheight((*root)->right->right) >= getheight((*root)->right->left))
			{
				//Please reference 'AVLTree insert' chapter, this is the case 2
				left_rotate(root);
			}
			else{
				//Please reference 'AVLTree insert' chapter, this is the case 4
				right_rotate(&(*root)->right);
				left_rotate(root);
			}
		}
	}

	//Update the current node height
	(*root)->height = MAX(getheight((*root)->left), getheight((*root)->right)) + 1;
	return 0x0;
}


/*
 * return: 0---find successful   1---find failure
 */
int find(AVLTree root, int data)
{
	if (!root)
		return -1;
	else if(root->data == data)
		return 0;
	else if(root->data < data)
		return find(root->right, data);
	else
		return find(root->left, data);
}

//The following function is just an internal helper function
static inline void destroy_postorder(AVLTree root)
{
	if(!root)
		return;
	destroy_postorder(root->left);
	destroy_postorder(root->right);
	free(root);
}

int destroy(AVLTree *root)
{
	if(!*root)
		return 0;

	destroy_postorder(*root);
	*root = NULL;
	return 0x0;
}


void inorder_traverse(AVLTree root)
{
     if(!root)
	 	return;
	 inorder_traverse(root->left);
	 printf("%d ", root->data);
	 inorder_traverse(root->right);
}

void preorder_traverse(AVLTree root)
{
	if(!root)
		return;

	printf("%d ", root->data);
	preorder_traverse(root->left);
	preorder_traverse(root->right);
}

void postorder_traverse(AVLTree root)
{
	if(!root)
		return;

	postorder_traverse(root->left);
	postorder_traverse(root->right);
	printf("%d ", root->data);

}

5.3 测试代码

如下是测试代码main.c:

#include <stdio.h>
#include <stdlib.h>
#include "avltree.h"


int main(int argc,char *argv[])
{
	int a[] = {1,2,3,4,5,10,9,8,7,6};
	int i;

	AVLTree root = NULL;

	for (i = 0; i < sizeof(a)/sizeof(int); i++)
	{
		if(insert_node(&root, a[i]) != 0)
		{
			printf("insert node failure\n");
			return -1;
		}
	}

	inorder_traverse(root);
	printf("\n");

	remove_node(&root, 3);
	remove_node(&root, 5);
	inorder_traverse(root);
	printf("\n");


	insert_node(&root, 100);
	insert_node(&root, -100);
	insert_node(&root, -1);
	inorder_traverse(root);
	printf("\n");

	destroy(&root);

	inorder_traverse(root);
	printf("\n");
	return 0x0;
}

编译运行：

# gcc -g -o avltree main.c avltree.c
# ./avltree 
1 2 3 4 5 6 7 8 9 10 
1 2 4 6 7 8 9 10 
-100 -1 1 2 4 6 7 8 9 10 100

[参看]:

Ivanzz

发上等愿，结中等缘，享下等福；择高处立，寻平处住，向宽处行