AVL树原理及实现（二）

我们在上一章中已经介绍了AVL树的原理及实现，在这一章我们再通过一个例子来加深对AVL树的理解。

1. AVL树的构造

前面我们已经讲述过了AVL树的定义及相关性质，关于如何构造二叉排序树，我们这里再给出一个例子。参看如下图：

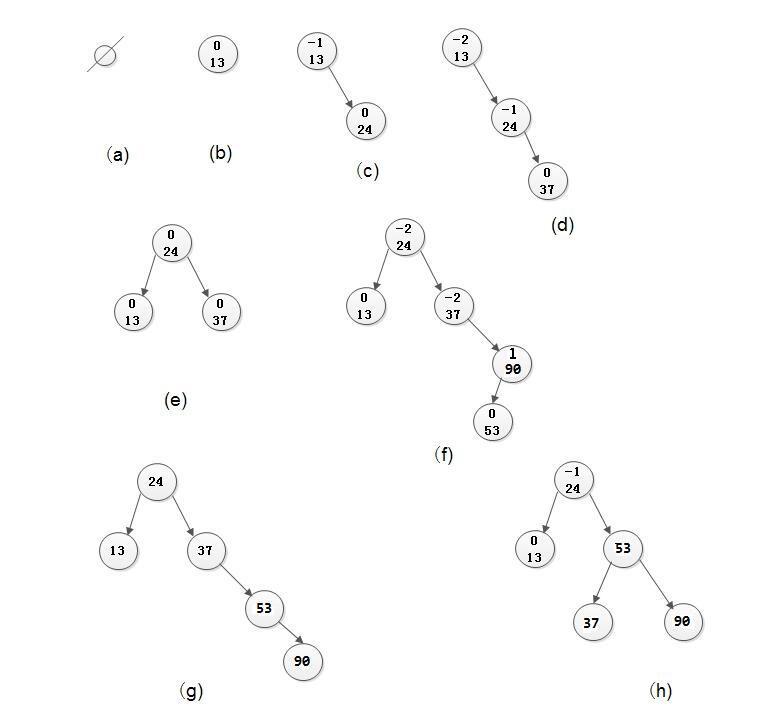
avl-construct-example

假设表中关键字序列为(13,24,37,90,53)。空树和1个节点13的树显然都是平衡的二叉树。在插入24之后仍是平衡的，只是根节点的平衡因子BF由0变为-1；在继续插入37之后，由于节点13的BF值由-1变成-2，由此出现了不平衡的现象。此时好比一根扁担出现一头重一头轻的现象，若能将扁担的支撑点由13改至24，扁担的两头就平衡了。由此，可以对树作一个向左逆时针“旋转”的操作，令节点24为根，而节点13为它的左子树，此时， 节点13和节点14的平衡因子都为0，而且保持二叉排序树的特性。在继续插入90和53之后，由于节点37的BF值由-1变成-2，排序树中出现了新的不平衡现象，需进行调整。但此时由于节点53插在节点90的左子树上，因此不能如上作简单调整。对于以节点37为根的子树来说，既要保持二叉排序树的特性，又要平衡，则必须以节点53作为根节点，而使节点37成为它的左子树的根，节点90成为它的右子树的根。这好比对树作了两次“旋转”操作———先向右顺时钟，后向左逆时钟（见上图(f)~(h))，使二叉排序树由不平衡转化为平衡。

一般情况下，假设由于二叉排序树上插入节点而失去平衡的最小子树根节点的指针为x(即 x 是离插入节点最近，且平衡因子绝对值超过1的祖先节点），则失去平衡后进行调整的规律可归纳为下列4种情况：

(1) 情形1

单向右旋平衡处理：由于在*x的左子树根节点的左子树上插入节点，*x的平衡因子由1增至2，致使以*x为根的子树失去平衡，则需进行一次向右的顺时针旋转操作。此种情形就是所谓的LL型。

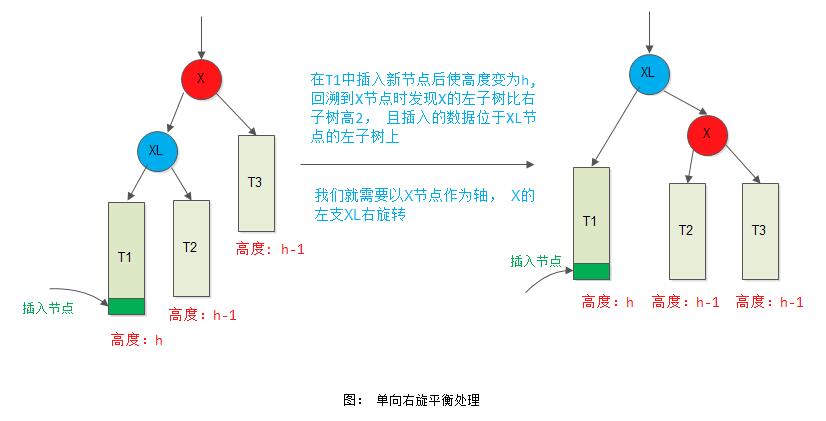
ds-avl-right-rotate

(2) 情形2

单向左旋平衡处理：由于在*x的右子树根节点的右子树上插入节点， *x的平衡因子由-1变为-2，致使以*x为根节点的子树失去平衡，则需进行一次向左的逆时钟旋转操作。此种情形就是所谓的RR型。

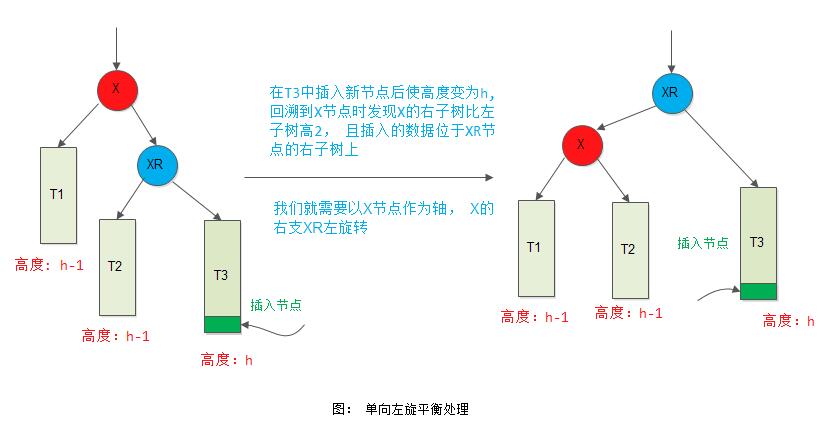
ds-avl-left-rotate

(3) 情形3

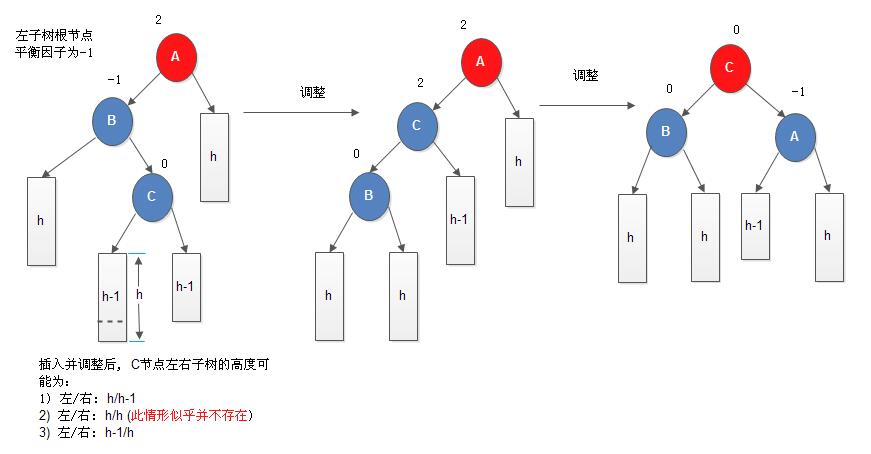
双向旋转（先左后右)平衡处理：由于在*x的左子树根节点的右子树上插入节点，*x的平衡因子由1增至2，致使以*x为根节点的子树失去平衡，则需进行两次旋转（先左旋后右旋）操作。此种情形就是所谓的LR型。

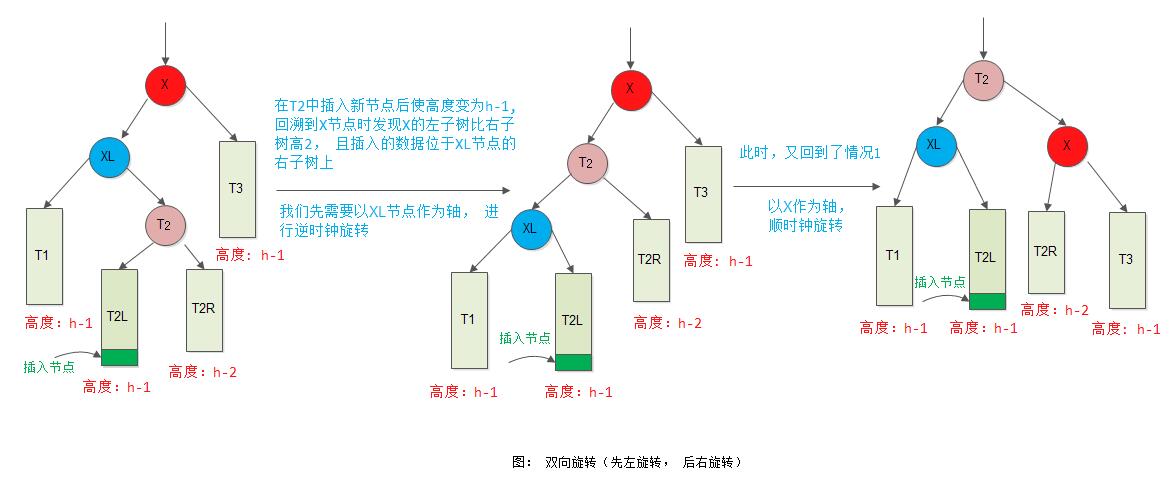
ds-avl-left-right-rotate

(4) 情形4

双向旋转（先右后左)平衡处理: 由于在*x的右子树根节点的左子树上插入节点， *x的平衡因子由-1变为-2，致使以*x为根节点的子树失去平衡，则需进行两次旋转(先右旋后左旋）操作。此种情形就是所谓的RL型。

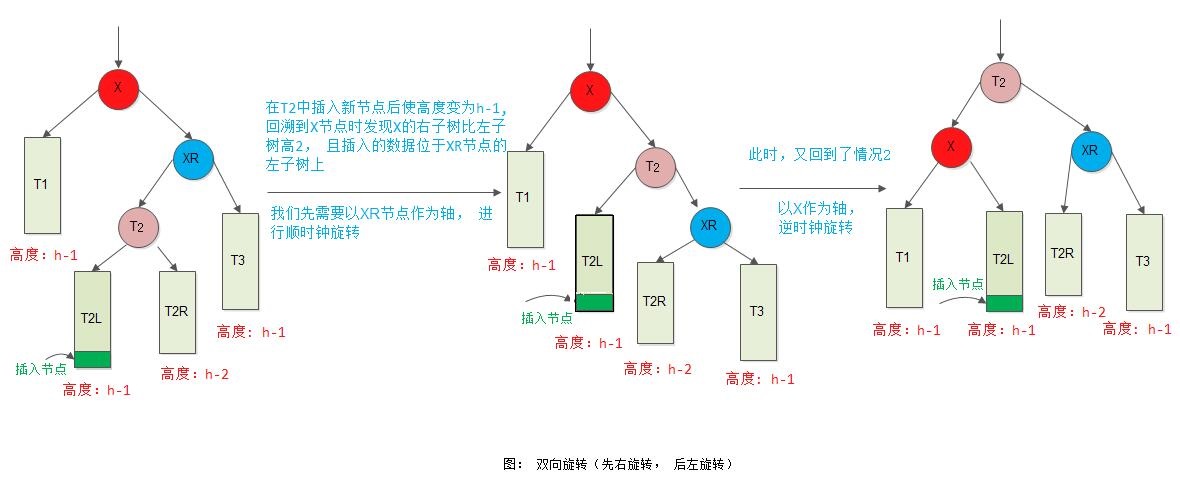
ds-avl-right-left-rotate

上述4种情况中，(1)和(2)对称，(3)和(4)对称。旋转操作的正确性容易由“保持二叉排序树的特性：中序遍历所得的关键字序列自小至大有序”证明之。由上面示意图可见，无论哪一种情况，都可以通过旋转达到平衡。因此，当平衡的二叉排序树因插入节点而失去平衡时，仅需对最小不平衡子树进行平衡旋转处理即可。因为经过旋转处理之后的子树深度和插入之前相同，因而不影响插入路径上所有祖先节点的平衡度。

2. AVL树插入算法

在平衡的二叉排序树BBST上插入一个新的数据元素e的递归算法可描述如下：

(1) 若BBST为空树，则插入一个数据元素为e的新节点作为BBST的根节点，树的深度增1；

(2) 若e的关键字和BBST的根节点的关键字相等，则不进行插入；

(3) 若e的关键字小于BBST的根节点的关键字，而且在BBST的左子树中不存在和e有相同关键字的节点，则将e插入在BBST的左子树上，并且当插入之后的左子树深度增加(+1)时，分别就下列不同情况处理之：

BBST的根节点的平衡因子为-1（右子树的深度大于左子树的深度）：则将根节点的平衡因子更改为0，BBST的深度不变；

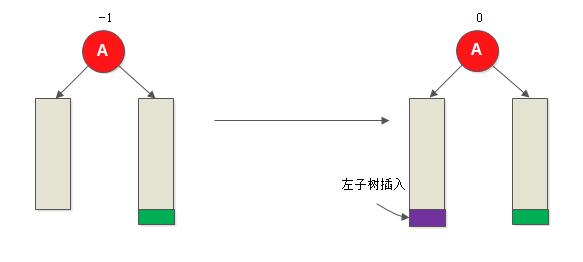
ds-avl-insert-left1

BBST的根节点的平衡因子为0（左、右子树的深度相等）：则将根节点的平衡因子更改为1，BBST的深度增加1；

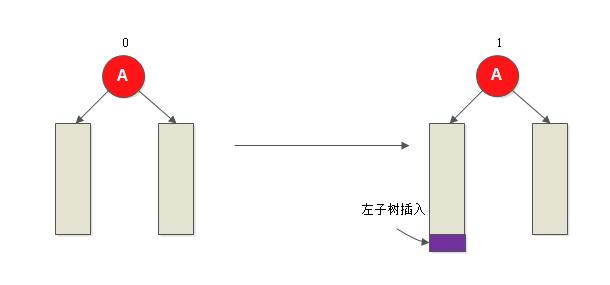
ds-avl-insert-left2

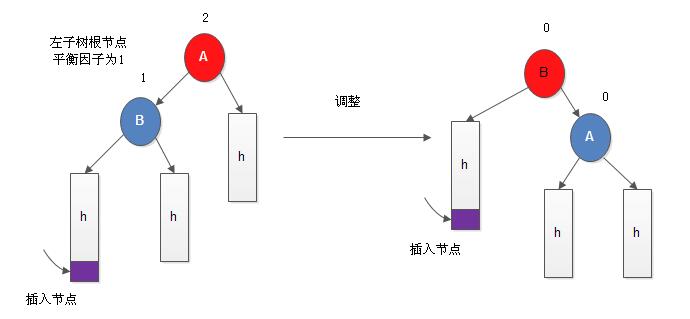
BBST的根节点的平衡因子为1（左子树的深度大于右子树的深度）：若BBST的左子树根节点的平衡因子为1，则需进行单向右旋平衡处理，并且在右旋处理之后，将根节点和其右子树根节点的平衡因子更改为0，树的深度不变；若BBST的左子树根节点的平衡因子为-1，则进行先向左、后向右的双向旋转平衡处理，并且在旋转处理之后，修改根节点和其左、右子树根节点的平衡因子，树的深度不变；

ds-avl-insert-left31

ds-avl-insert-left32

(4) 若e的关键字大于BBST的根节点的关键字，而且在BBST的右子树中不存在和e有相同关键字的节点，则将e插入在BBST的右子树上，并且当插入之后的右子树深度增加(+1)时，分别就不同情况处理之。其处理操作和（3）中所述相对称。

3. AVL树实现示例

3.1 相关头文件

头文件avltree.h:

#ifndef __AVL_TREE_H_
#define __AVL_TREE_H_


#define LH	1
#define EH	0
#define RH	-1


#define TRUE	1
#define FALSE	0

typedef struct BSTNode{
	int data;
	int bf;				//the balance factor
	struct BSTNode *left;
	struct BSTNode *right;

}BSTNode, *BSTree;



int InsertAVL(BSTree *root,int e, int *taller);




#endif

3.2 源文件

源文件avltree.c:

#include <stdio.h>
#include <stdlib.h>
#include "avltree.h"


static void right_rotate(BSTree *node)
{
	BSTNode *top = *node;
	BSTNode *left = (*node)->left;


	top->left = left->right;
	left->right = top;

	*node = left;
}

void left_rotate(BSTree *node)
{
	BSTNode *top = *node;
	BSTNode *right = (*node)->right;

	top->right = right->left;
	right->left = top;

	*node = right;
}

static void left_balance(BSTree *node)
{
	BSTNode *left = (*node)->left;

	switch(left->bf)
	{
		case LH:
			left->bf = EH;
			(*node)->bf = EH;
			right_rotate(node);
			break;
		case RH:
			BSTNode *lright = left->right;
			switch(lright->bf)
			{
				case LH:
					(*node)->bf = RH;
					left->bf = EH;
					break;
				case EH:      //此处只有原来lright为NULL的情况，新插入之后才会出现平衡因子为EH(即新插入节点为lright本身)
					(*node)->bf = left->bf = EH;   
					break;
				case RH:
					(*node)->bf = EH;
					left->bf = LH;
					break;
			}

			lright->bf = EH;
			left_rotate(&(*node)->left);
			right_rotate(node);
	}
}

static void right_balance(BSTree *node)
{
	BSTNode *right = (*node)->right;

	switch(right->bf)
	{
		case RH:
			(*node)->bf = EH;
			right->bf = EH;
			left_rotate(node);
			break;
		case LH:
			BSTNode *rleft = right->left;

			switch(rleft->bf)
			{
				case LH:
					(*node)->bf = EH;
					right->bf = RH;
					break;
				case EH:
					(*node)->bf = right->bf = EH;
					break;
				case RH:
					(*node)->bf = LH;
					right->bf = EH;
					break;
					
			}
			rleft->bf = EH;
			right_rotate(&(*node)->right);
			left_rotate(node);
			
	}
}


int InsertAVL(BSTree *root,int e, int *taller)
{
	if(!*root)
	{
		BSTNode *node = (BSTNode *)malloc(sizeof(BSTNode));
		if(!node)
			return -1;

		node->data = e;
		node->bf = EH;
		node->left = node->right = NULL;

		*root = node;

		*taller = TRUE;			//

		return 0x0;
	}
	else if((*root)->data == e)
	{
		*taller = FALSE;
		return -1;
	}
	else if(e < (*root)->data)
	{
		if(InsertAVL(&(*root)->left, e, taller) != 0)
			return -1;

		if(*taller)
		{
			switch((*root)->bf)
			{
				case LH:
					left_balance(root);
					*taller = FALSE;
					break;
				case EH:
					(*root)->bf = LH;
					*taller = TRUE;
					break;
				case RH:
					(*root)->bf = EH;
					*taller = FALSE;
					break;
			}
		}
	}
	else{
		if(InsertAVL(&(*root)->right, e, taller) != 0)
			return -1;

		if(*taller)
		{
			switch((*root)->bf)
			{
				case LH:
					(*root)->bf = EH;
					*taller = FALSE;
					break;
				case EH:
					(*root)->bf = RH;
					*taller = TRUE;
					break;
				case RH:
					right_balance(root);
					*taller = FALSE;
					break;
			}
		}
	}

	return 0x0;
}

3.3 BBST树节点的删除

这里我们仿照于插入，可以写出删除的源代码：

int findmin(BSTNode *node){
	if(!node){
		return -1;
	}
	
	while(node->left)
		node = node->left;
		
	return node->data;
}

int remove_node(BSTree *node, int data, int *shorter){
	if(!*node){
		*shorter = FALSE;
		return -1;
	}
	
	if((*node)->data == data){
		if((*node)->left != NULL && (*node)->right != NULL){
			int key = findmin((*node)->right);
			(*node)->data = key;
			
			if(remove_node(&(*node)->right, key, shorter) < 0)
				return -1;
				
			if(*shorter == TRUE){
				switch((*node)->bf){
					case LH:
						right_balance(node);
						*shorter = FALSE; 
					case EH:
						(*node)->bf = LH;
						*shorter = FALSE;
						break;
					case RH:
						(*node)->bf = EH;
						*shorter = TRUE;
						break;
				}
			}
			
		}else if((*node)->left == NULL){
			BSTNode *t = *node;
			(*node) = (*node)->right;
			free(t);
			
			*shorter = TRUE;
			return 0x0;
		}else{
			BSTNode *t = *node;
			(*node) = (*node)->left;
			free(t);
			
			*shorter = TRUE;
			return 0x0;
		}
	
	
	}else if((*node)->data > data){
		if(remove_node(&(*node)->left, data, shorter) < 0)
			return -1;
		
		if(*shorter == TRUE){
			switch((*node)->bf){
				case LH:
					(*node)->bf = EH;
					*shorter = TRUE;
					break;
				case EH:
					(*node)->bf = RH;
					*shorter = FALSE;
					break;
				case RH:
					left_balance(node);
					*shorter = FALSE;
					break;
			}
		
		}	
			
	}else{
		if(remove_node(&(*node)->right, data, shorter) < 0)
			return -1;
		
		if(*shorter == TRUE){
			switch((*node)->bf){
				case LH:
					right_balance(node);
					*shorter = FALSE; 
				case EH:
					(*node)->bf = LH;
					*shorter = FALSE;
					break;
				case RH:
					(*node)->bf = EH;
					*shorter = TRUE;
					break;
			}
		}
	}
	
	return 0x0;
}

void inorder_tranverse(BSTree root)
{
	if(!root)
		return;

	inorder_tranverse(root->left);
	printf("%d ", root->data);
	inorder_tranverse(root->right);
}

3.4 BBST树的测试

#include <stdio.h>
#include <stdlib.h>
#include "avltree.h"


int main(int argc, char *argv[])
{
	BSTree root = NULL;
	int i;
	int taller, shorter;

	for(i = 10; i>0; i--)
		InsertAVL(&root, i, &taller);

	inorder_tranverse(root);
	printf("\n");

	remove_node(&root, 8, &shorter);
	remove_node(&root, 2, &shorter);

	inorder_tranverse(root);

	
	return 0;
}

编译测试：

# gcc -o avltree_test avltree.c avltree_test.c
# ./avltree_test 
1 2 3 4 5 6 7 8 9 10
1 3 4 5 6 7 9 10

[参看]:

Ivanzz

发上等愿，结中等缘，享下等福；择高处立，寻平处住，向宽处行