红黑树的原理及实现

本文我们主要介绍一下红黑树的实现原理。在了解红黑树之前，请先参看2-3树以及avl树的相关实现。

1. 红黑树

红黑树(Red-Black Tree)是一种自平衡二叉查找树。是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树(symmetric binary B-trees)。后来，在1978年被Leo J. Guibas和Robert Sedgewich修改为如今的红黑树。红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。它虽然复杂，但它的最坏情况运行时间也是非常好的，并且在实践中是高效的：它可以在O(logn)时间内做查找、插入和删除操作，这里n是树中元素的数目。

1.1 数据结构

红黑树的统计性能要好于平衡二叉树(即AVL树），因此红黑树在很多地方都有应用。在C++ STL中，很多部分（包括set、multiset、map、multimap）应用了红黑树的变体（SGI STL中的红黑树有一些变化，这些修改提供了更好的性能，以及对set操作的支持）。其他的平衡树还有： AVL树、SBT树、伸展树、TREAP树。

1.2 红黑树的性质

红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树一般的要求外，对于任何有效的红黑树我们增加了如下的额外要求：

性质1：节点是红色或黑色
性质2：根节点是黑色
性质3：每个叶节点(nil节点, 空节点)是黑色的。注意：这里的叶子节点是nil叶子
性质4：每个红色节点的两个子节点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色节点）
性质5：从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

注意： 
1） 红黑树中的叶子节点均指nil叶子

2） 性质5确保没有一条路径会比其他路径长出2倍。因而，红黑树是相对接近平衡的二叉树

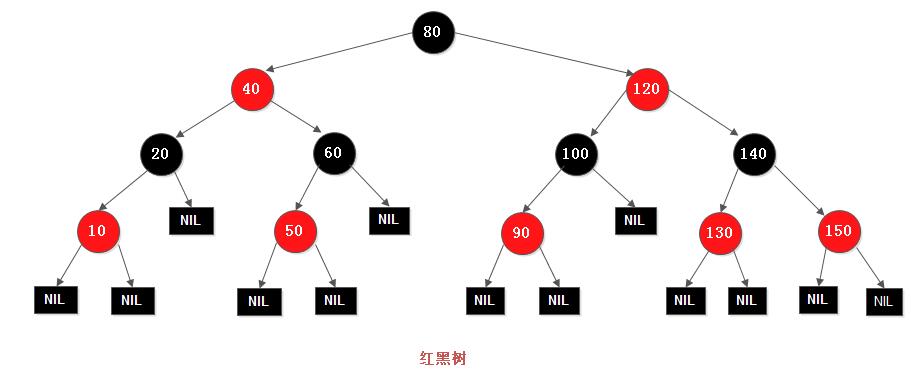
正是由于上面的这些约束产生了红黑树的关键性质：从根到叶子的最长的可能路径不多于最短的可能路径的两倍。结果是这棵树大致上是平衡的。因为如插入、删除和查找某个值的在最坏情况下的时间复杂度为树的高度，这个高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

要知道为什么这些特性确保了这个结果，我们注意到性质4导致了路径不可能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。

1.3 红黑树与2-3树

红黑树的另一种定义是满足下列条件的二叉查找树：

红链接均为左链接
没有任何一个节点同时和两条红链接相连
该树是完美黑色平衡的，即任意空链接到根节点的路径上的黑色链接数量相同

如果我们将一个红黑树中的红链接画平，那么所有的空链接到根节点的距离都是相同的；如果我们将由红链接相连的节点合并，得到的就是一棵2-3树。相反，如果将一棵2-3树中的3-节点画作由红色左链接相连的两个2-节点, 那么不会存在能够和两条红链接相连的节点，且树必然是完美平衡的。

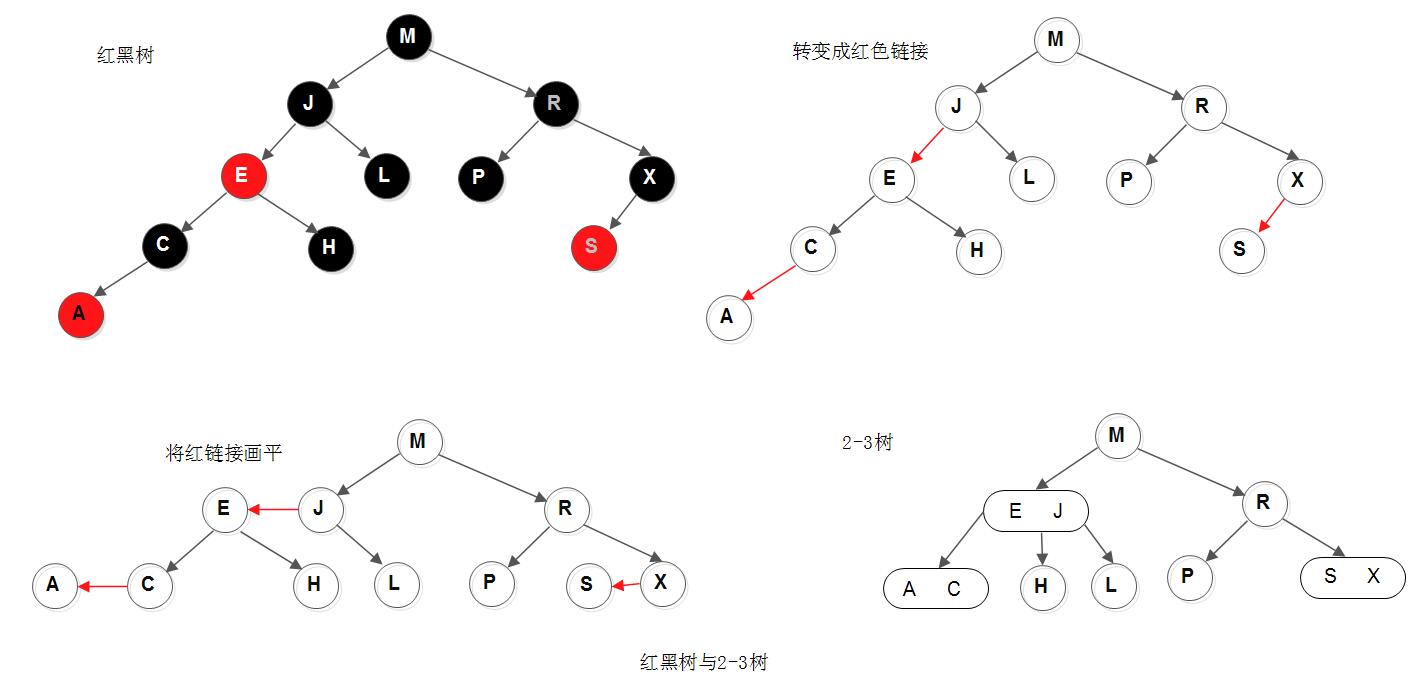
注：其实上面只是将红黑树中的红色左链接进行了画平，如果将红色右链接也进行画平，得到的是一颗2-3-4树

2. 旋转的定义

因为很多书中对旋转的定义不一致，所以我们有必要在这里说明一下。假设红黑树节点数据结构如下：

#define COLOR_RED  0x0
#define COLOR_BLACK 0x1

typedef struct RBNode{
   int key;
   unsigned char color;
   struct RBNode *left;
   struct RBNode *right;
   struct RBNode *parent;
}rb_node_t, *rb_tree_t;

以某一节点为轴，它的左枝顺时针旋转，作为新子树的根，我们称之为顺时针旋转（clockwise)或者右旋转;

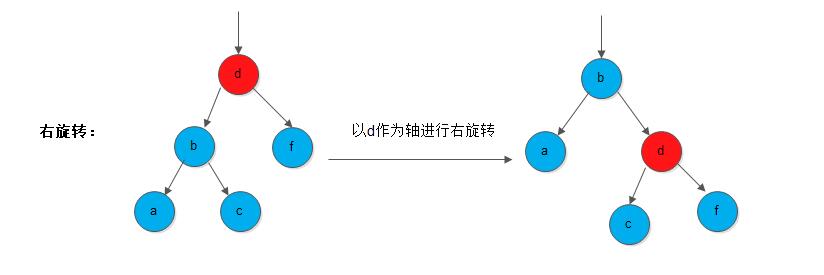
源代码如下：

static rb_node_t *rb_rotate_right(rb_tree_t *root, rb_node_t *node)
{
    rb_node_t *left = node->left;

    if(node->left = left->right)
    {
       left->right->parent = node;
    }

    left->right = node;
   
    if(left->parent = node->parent)
    {
       if(node->parent->left == node)
       {
          node->parent->left = left;
       }
       else{
          node->parent->right = left;
       }
    }
    else{
       *root = left;
    }
   
    node->parent = left;
    return left;
}

以某一节点为轴，它的右枝逆时针旋转，作为新子树的根，我们称为逆时钟旋转(anti clockwise)或者左旋转;

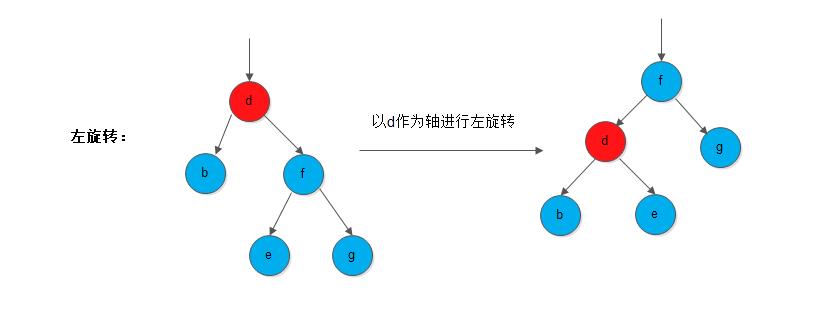
源代码如下：

static rb_node_t *rb_rotate_left(rb_tree_t *root, rb_node_t *node)
{
    rb_node_t *right = node->right;

    if(node->right = right->left)
    {
       right->left->parent = node;
    }
    
    right->left = node;
    
    if(right->parent = node->parent)
    {
        if(node->parent->left == node)
        {
             node->parent->left = right;
        }
        else{
             node->parent->right = right;
        }
    }
    else{
       *root = right;
    }

    node->parent = right;
    return right;
}

3. 红黑树节点的插入

3.1 插入的基本原理

和AVL树一样，在插入和删除节点之后，红黑树也是通过旋转来调整树的平衡的。红黑树插入节点z的方法和普通二叉搜索树一样，都是将新节点z作为一个叶子节点插入到树的底部。不同的是，红黑树将新节点z作为一个红色节点，将其孩子指针指向nil叶子, 然后当新节点z的父节点为红色时，由于违反了性质4，因此需要对其进行调整（如果新节点z的父节点为黑色，且z本身是红色，因此不会违反任何性质）。

红黑树调整算法的设计要遵循一个原则： 同一时刻红黑树只能违反最多一条性质。

红黑树插入节点z后的调整有3种情况：

(1) z的叔节点y是红色的

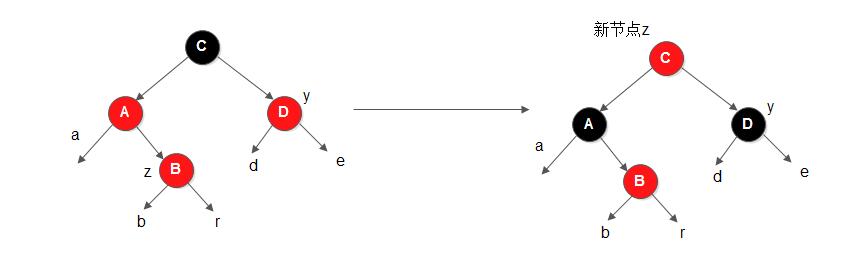
左图中插入的新节点z是一个红色节点，其父节点A是红色的，违反了性质4，所以需要进行调整（由于节点A是红色的，根据性质4，因树本身是平衡的，所以节点C必然是黑色的）。因为其叔节点y是红色的，于是可以修改节点A、节点D为黑色，此时节点C的黑高就会发生变化，从原来的1（忽略子树a、b、r、d、e的黑高）变成了2，因此还需要将节点C变成红色以保持其黑高不变。此时，由于节点C由黑色变成了红色，如果节点C的父节点是红色，那么会违反性质4，于是节点C变成了新的节点z，从这里开始向上回溯调整树。

注意：

对于新插入的节点z是节点A的左子树的情况与上述一致；
对于新插入的节点z是节点C的右子树的节点的情况与上述对称；

情况1是一种比较简单的情况。

(2) z的叔节点y是黑色，且z是一个右孩子

情况2不能像情况1那样通过修改z的父节点的颜色来维持性质4，因为如果将z的父节点变成了黑色，那么树的黑高就会发生变化，必然会引起对性质5的违反。以上面情况1的图为例，假设此时节点y为黑色，那么节点C的右子树高度为2（忽略子树d和e），左子树高也相同（因为树是平衡的），如果简单的修改节点A为黑色，那么节点C的左子树的黑高会比右子树大1，此时即使将节点C修改为红色也于事无补。

此时可以通过旋转节点z的父节点使情况2变成情况3进行处理。

注： 此种情况只可能在调整过程中出现

(3) z的叔节点是黑色，且z是一个左孩子

情况2转变成情况3, 然后针对情况3进行处理的流程如下：

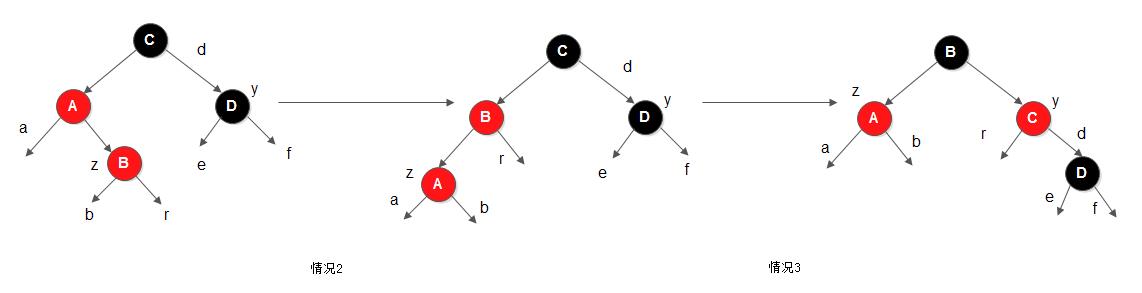
情况2通过对节点A进行一次左旋转变成情况3，此时节点z不再是原来的B，而是节点A了，此时树依然只是违反性质4。情况3通过对节点C进行了一次右旋转，然后改变节点B和节点C的颜色，得到右图。

注： 情况3也只可能在调整过程中出现

先来证明这以操作的正确性：

对于左图，由于刚插入节点z的时候，只违反了性质4，性质5依然满足，假设子树a的黑高为ha，子树b的黑高为hb，依次类推，可知道ha==hb==hr==hd, hC=hd+1, 对节点A进行左旋转变成情况3（即中图），树依然只违反性质4，新的节点z变为节点A。之后再对节点C进行右旋转并修改颜色得到右图，此时节点A和节点C是平衡的，节点B也是平衡的，而且节点B的黑高为hd+1。由此可知，整个操作后，该树的黑高不变，且满足所有红黑树的性质。

在红黑树的调整过程中，z始终指向一个红色节点，因此z永远不会影响其所在树的黑高，于是我们始终关注节点z的父节点是否为红色，如果是则意味着违反了性质4，需要进行调整；否则，就可以退出循环了。在算法的最后，我们还需要关注性质2，将根节点的颜色改为黑色，根节点的颜色改变也是绝对不会引起树的不平衡的，而将其改为黑色也是不会引起对性质4的违反的。

3.2 插入相关算法

int rb_insert_fixup(rb_tree_t *root, rb_node_t *node)
{
	rb_node_t *parent;
	rb_node_t *grand_parent;

	//If parent exist, and the color of parent is RED
	while((parent = node->parent) && parent->color == COLOR_RED)
	{
		grand_parent = parent->parent;

		//parent node is grand_parent node's left child(grand_parent should not be NULL, because parent->color==COLOR_RED)
		if(grand_parent->left == parent)
		{
			rb_node_t *uncle = grand_parent->right;

			//Case 1: uncle is RED
			if(uncle && uncle->color == COLOR_RED)
			{
				parent->color = COLOR_BLACK;
				uncle->color = COLOR_BLACK;
				grand_parent->color = COLOR_RED;
				
				node = grand_parent;
				continue;
			}

			//Case 2: uncle is BLACK, and node is parent's right child
			if(parent->right == node)
			{
				rb_rotate_left(root, parent);
				
				// reset parent and node pointer
				rb_node_t *tmp;
				tmp = parent;
				parent = node;
				node = tmp;
				
				//Here successful convert Case 2 to Case3
			}

			//Case 3: uncle is BLACK, and node is parent's left child
			parent->color = COLOR_BLACK;
			grand_parent->color = COLOR_RED;
			rb_rotate_right(root, grand_parent);

		}
		else{
			rb_node_t *uncle = grand_parent->left;
			
			//Case 1: uncle is RED
			if(uncle && uncle->color == COLOR_RED)
			{
				parent->color = COLOR_BLACK;
				uncle->color = COLOR_BLACK;
				grand_parent->color = COLOR_RED;
				
				node = grand_parent;
				continue;
			}

			//Case 2: uncle is BLACK, and node is parent's left child
			if(parent->left == node)
			{
			rb_rotate_right(root,parent);
			
				//reset parent and node pointer
				rb_node_t *tmp;
				tmp = parent;
				parent = node;
				node = tmp;
				
				//Here success convert Case 2 to Case 3
			}

			//Case 3: uncle is BLACK, and node is parent's right child
			parent->color = COLOR_BLACK;
			grand_parent->color = COLOR_RED;
			rb_rotate_left(root, grand_parent);
		}
	}

	(*root)->color = COLOR_BLACK;
	return 0x0;
}


int insert_rbtree(rb_tree_t *root, rb_node_t *node)
{
	rb_node_t *p = *root;
	rb_node_t *q = NULL;

	//find the position we need to insert
	while(p)
	{
		q = p;
		if(p->key == node->key)
			return 1;
		else if(p->key > node->key)
			p = p->left;
		else
			p = p->right;
	}

	node->parent = q;

	if(q != NULL)
	{
	    if(node->key < q->key)
			q->left = node;
		else
			q->right = node;
	}
	else{
		*root = node;
	}

	node->color = COLOR_RED;

	return rb_insert_fixup(root, node);
}

4. 红黑树节点的删除

4.1 删除的基本原理

红黑树只有在黑色节点被删除的时候才需要进行调整，因为只有这种情况下才会引起对性质5的违反（或许还有性质4)。

红黑树也是一种二叉搜索树，因此在删除红黑树一个节点的时候，首先要执行二叉搜索树的删除过程；然后再针对删除后可能会违反的红黑树性质，通过旋转和重新着色等一些列操作来修正该树，使之重新成为一棵红黑树。

(1) 二叉搜索树删除

针对二叉搜索树删除节点的3种情况:

如果节点z没有孩子节点，那么只需要简单的将其删除即可，并修改父节点，用NULL来替换z；
如果节点z只有一个孩子，那么将孩子节点提升到z的位置，并修改z的父节点，用z的孩子替换z；
如果节点z有两个孩子，那么查找z的后继y，此外后继一定在z的右子树中，然后让y替换z

这三种情况中，前两种较为简单，3相对棘手，我们通过示意图描述这几种情况：

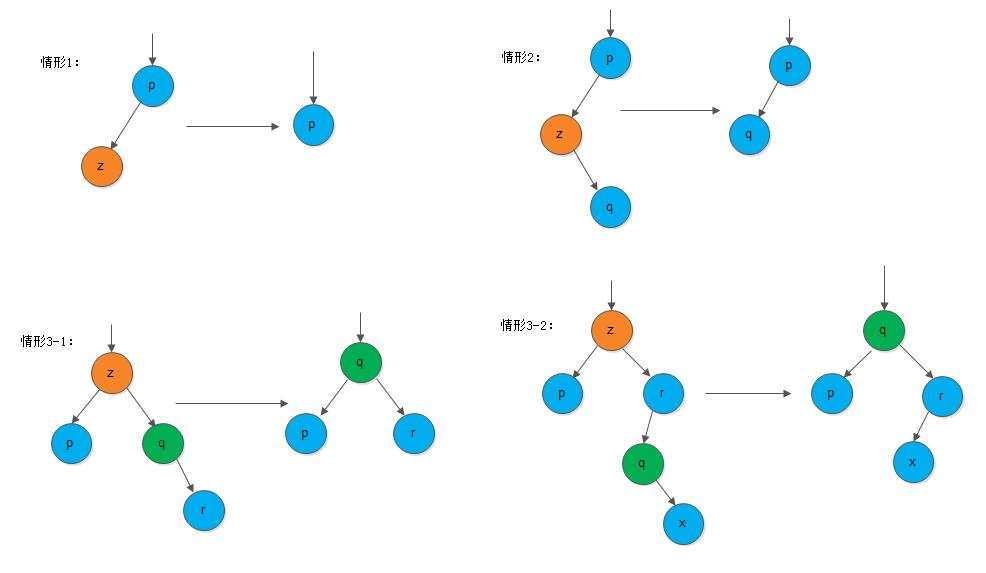从上图我们可以看到，针对情形3，又可以分出两种子情形：

(1) z的后继q位于右子树中，但没有左孩子

(2) z的后继q位于右子树中，但是并不是z的右孩子, 此时要用q的右孩子替换z

下面我们给出相关源码：

int delete_rbtree(rb_tree_t *root, int key)
{
	rb_node_t *p = *root;
	
	//find the node
	while(p)
	{
		if(p->key == key)
			break;
		else if(p->key > key)
			p = p->left;
		else
			p = p->right;
	}
	
	if(!p)
		return -1;


	if(p->left && p->right)
	{
		//get successor node
		rb_node_t *successor = p->right;
	
		while(successor->left)
			successor = successor->left;
	
		if(p->parent)
		{
			if(p->parent->left == p)
				p->parent->left = successor;
			else
				p->parent->right = successor;
		}
		else{
			*root = successor;
		}
	
		rb_node_t *successor_child = successor->right;
		rb_node_t *successor_parent = successor->parent;
		int color = successor->color;      //save the color
		
		if(successor_parent == p)
		{
			successor_parent = successor;
		}
		else{
			if(successor_child)
				successor_child->parent = successor_parent;
		
			successor_parent->left = successor_child;
		
			successor->right = p->right;
			p->right->parent = successor;
		}

		successor->parent = p->parent;
		successor->color = p->color;
		successor->left = p->left;
		p->left->parent = successor;
	
		if(color == COLOR_BLACK)
			rbtree_delete_fixup(root, successor_child, successor_parent);
	
		free(p);
		return 0x0;
	
	}


	rb_node_t *child = NULL;
	rb_node_t *parent = NULL;
	int color;
	
	if(p->left)
		child = p->left;
	else
		child = p->right;
	
	
	parent = p->parent;
	color = p->color;   //save the color
	
	if(child)
		child->parent = parent;
	
	if(parent)
	{
		if(parent->left == p)
			parent->left = child;
		else
			parent->right = child;
	}
	else{
		*root = child;
	}
	
	
	if(color == COLOR_BLACK)
		rbtree_delete_fixup(root, child, parent);
	
	free(p);
	
	return 0x0;
}

注意：上面无论哪一种情况，得到的替换后的节点(即successor_child或child节点)都是平衡的，因为它到达叶子节点的路径都不经过被删节点（如果被替换的节点为黑色节点，那么该节点的父节点就会因为被删去了一个节点而失去平衡)。

4.2 删除后红黑树的调整

下面我们主要讲述一下，在被删节点为黑色节点时，删除后应该重新调整，使之达到平衡。设x为被删节点的替换节点，即：

在被删节点的左子树为空时，x为被删节点的右孩子
在被删节点的右子树为空时， x为被删节点的左孩子
替换节点x是空节点（即删除的是终端节点)
在被删节点的左右子树均不为空时， x为被删节点中序遍历直接后继的右孩子

在上面的定义中，替换节点x一定是平衡的，而x的父节点由于删除了一个黑色节点，会导致左右子树的不平衡。假如这里x节点为红色节点，则直接将x节点变成黑色，这时整棵树是平衡的；而若x是黑色，要实现平衡，有如下四种情况：

注： 替换节点x为空节点时，仍可以当做如下四种情况来进行处理

1） x的兄弟节点w是红色的

删除节点后，x的父节点xp经过 x 到达叶子节点的路径的黑高产生变化，以xp为根的树不再平衡：

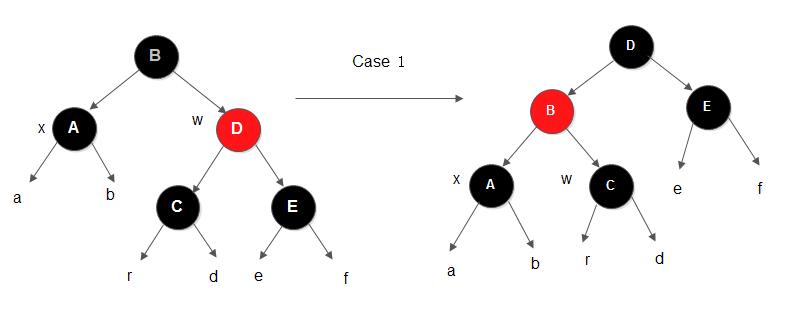
针对情况1， x是平衡的，但因为节点B的左子树被删去了一个黑色节点，导致节点B的左子树黑高少了1，所以节点B是不平衡的。此时， ha==hb==hr-1， hr==hd==he==hf。可以对节点B进行一次左旋，然后修改节点B和节点D的颜色，转变成情况2、3、4进行处理（上图转换后，x仍为A节点，B节点仍是不平衡的）

2) x的兄弟节点w是黑色的，并且w的两个子节点都是黑色的

如下图所示，这里又可以分成两种子情况：

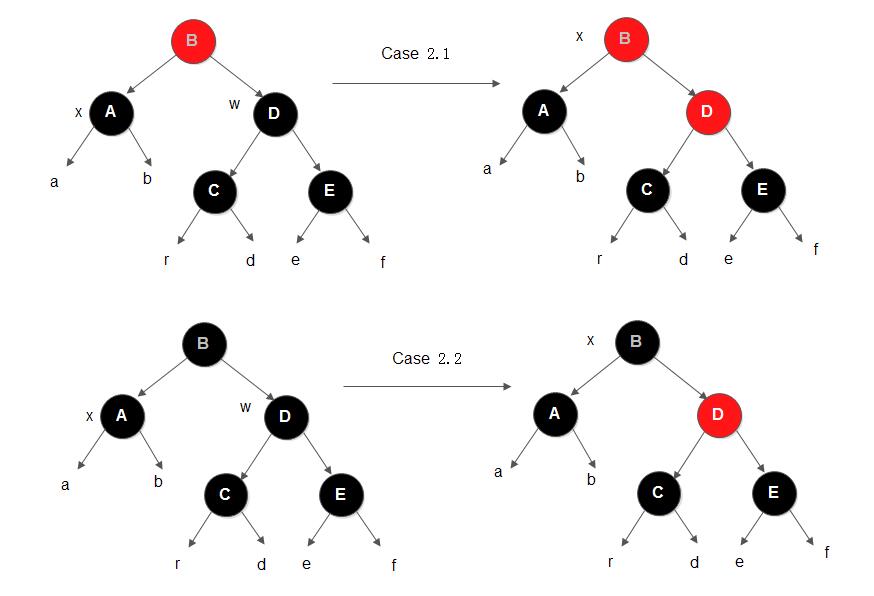
与情况1一样，在删除节点后，左图节点B不平衡，其中ha==hb==hr==hd==he==hf，B节点左子树的黑高为ha+1,右子树的黑高为hr+2，左子树黑高小于右子树黑高。于是我们可以直接修改节点D为红色，这样就可以使节点B达到平衡，但是这又会使得节点B的黑高比原来少1，会引起节点B往上的树不平衡。若此时B节点为红色（即上图Case2.1所示)，则直接将B节点修改为黑色，此时B的黑高又恢复如初，不影响其他树的平衡；而若节点B为黑色，则需要从该节点开始继续向上回溯调整树的黑高，此时B节点称为新的x节点。

3) x的兄弟节点w是黑色的，而且w的左孩子是红色的，w的右孩子是黑色的

这个和插入节点时的情况2类似，可以通过旋转将其转变成情况4进行处理。这里也有如下两种子情况：

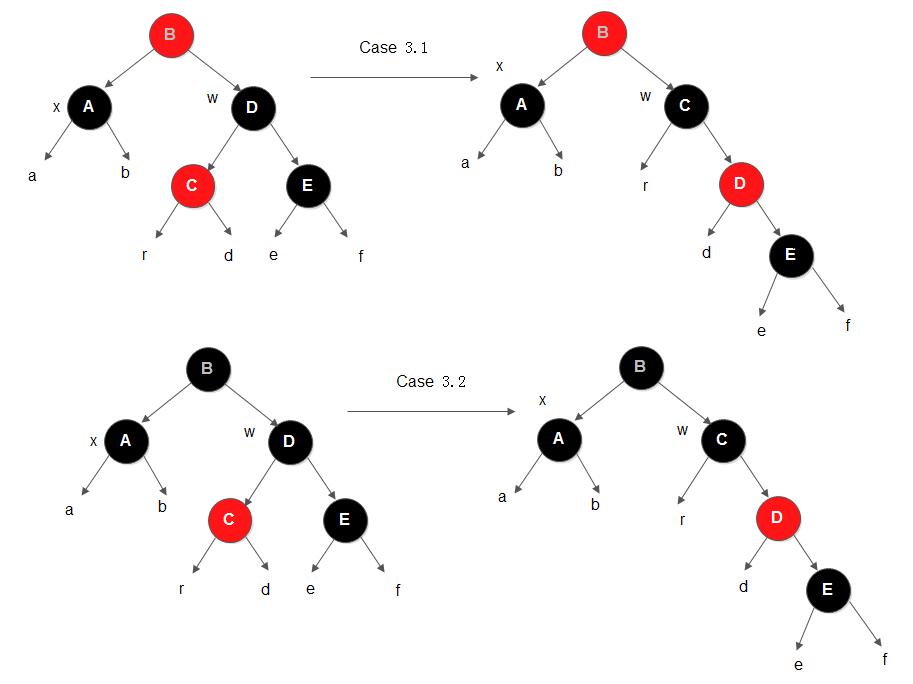
简单证明一下对节点w右旋转后节点w的红黑性质不会被破坏。旋转前，节点w是平衡的，所以hr==hd==he+1==hf+1。旋转后，节点w指向了节点C。此时，节点w的左子树高度为hr, 右子树的高度为he+1==hr，所以节点w依然是平衡的。再看节点D，左子树高度为hd，右子树高度为he+1==hd，所以节点D也是平衡的。综上所述，这一旋转操作不会影响节点B的右子树的红黑性质，仅仅将其转变成情况4进行处理而已。

4) x的兄弟节点w是黑色的，并且w的右孩子是红色的

对于这种情形，可以分为如下4种子情形：

情形4.1

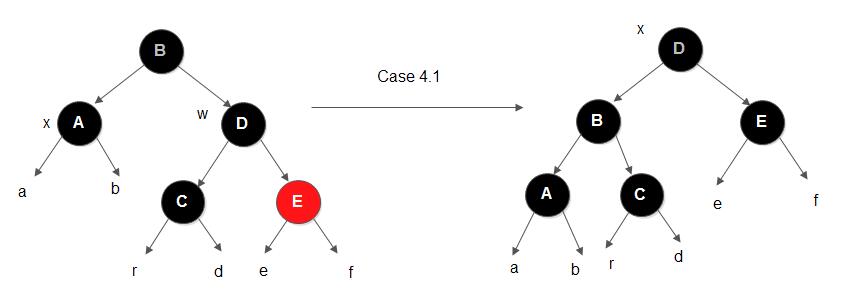
考察上图，因为删除节点导致节点B不平衡。其中，ha==hb==hr==hd，he==hf==ha+1。对节点B进行一次左旋转，同时修改节点D的颜色为其原父节点B的颜色，修改节点B的颜色为黑色（节点B颜色的修改可以直接修改，不用考虑当前B为红色还是黑色），节点E的颜色也修改成黑色（直接修改）。可以证得节点B已经达到平衡，同时节点D也达到平衡。并且该树从根开始的黑高在删除前和删除并旋转操作后不变，因此不会影响到其他树的平衡。也就是说，执行完情况4.1的操作之后，整棵树已经平衡了。

情形4.2

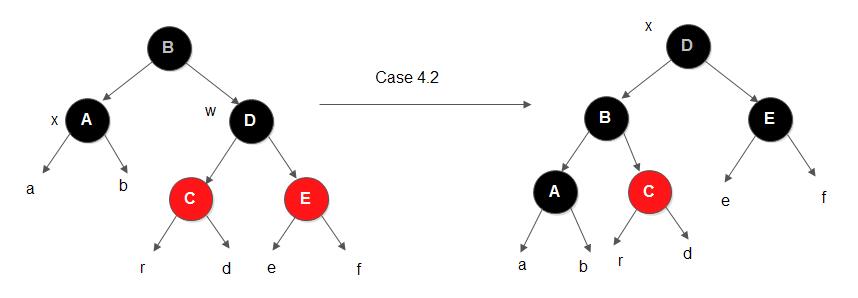
考察上面，ha==hb，hr==hd==he==hf==ha+1==hb+1。对节点B进行左旋转后，将D修改为与B相同的颜色（即更改成为其父节点的颜色），然后将节点B和节点E的颜色直接修改为黑色。可以证得，旋转后节点B是平衡的，节点D也是平衡的。并且该树从根开始的黑高在删除前和删除并旋转操作后不变，因此不会影响到其他树的平衡。也就是说，执行完情况4.2的操作之后，整棵树已经平衡了。

情况4.3

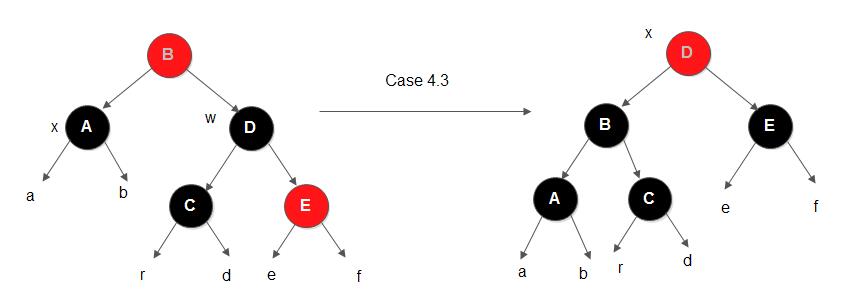
考察上图，ha==hb==hr==hd,he==hf==ha+1。对节点B进行左旋转后，将节点D修改为与节点B相同的颜色，然后将节点B和节点E的颜色直接修改为黑色。可以证得，旋转后节点B是平衡的，节点D也是平衡的。并且该树从根开始的黑高在删除前和删除并旋转操作后不变，因此不会影响到其他树的平衡。而除非旋转操作后，x节点为根节点，违反性质2，但是我们在x为根节点时就会退出循环，并且会直接再将x染成黑色，此时整棵树就平衡了。

情况4.4

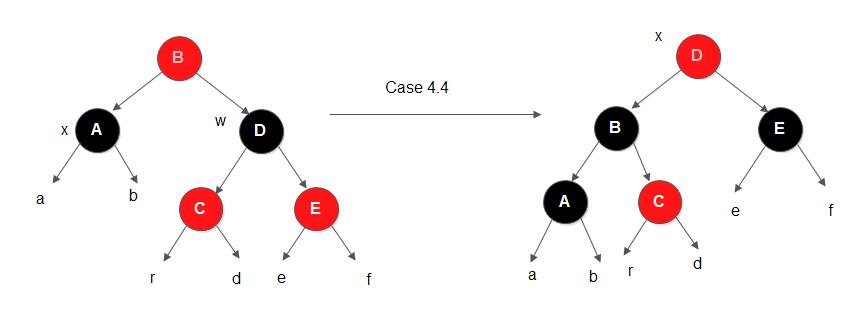
考察上图，hr==hd==he==hf, ha==hb==hr-1。对节点B进行左旋转，并将节点D修改为节点B相同的颜色，然后将节点B和节点E直接修改为黑色。可以证得，节点B是平衡的，节点D也是平衡的。并且该树从根开始的黑高在删除前和删除并旋转操作后不变，因此不会影响到其他树的平衡。而除非旋转操作后, x节点为根节点，违反性质2, 但是我们在x为根节点时就会退出循环，并且会直接再将x染成黑色，此时整棵树就平衡了。

注： 上述的1)、2）、3）、4）四种情况对节点x是一棵左子树而言的，当x是一棵右子树时其操作与上述操作完全对称。

下面给出删除修正操作的源代码：

static int rbtree_delete_fixup(rb_tree_t *root, rb_node_t *node, rb_node_t *parent)
{
	rb_node_t *brother = NULL;

	while((!node || node->color == COLOR_BLACK) && node != *root)
	{
	    if(parent->left == node)
	    {
			//The left branch


			//Note: brother can't be NULL, because we have delete a black node, 
			//and the tree is balanced before we delete the node
			brother = parent->right;

			if(brother->color == COLOR_RED)
			{
			    //1) Case 1: x's brother is COLOR_RED
				brother->color = COLOR_BLACK;
				parent->color = COLOR_RED;
				rb_rotate_left(root,node);
				brother = parent->right;
			}


			if((!brother->left || brother->left->color == COLOR_BLACK) &&
				(!brother->right || brother->right->color == COLOR_BLACK))
			{
			   //2) Case 2: x's brother is COLOR_BLACK, is its two child is NULL or COLOR_BLACK
			   brother->color = COLOR_RED;
			   node = parent;
			   parent = node->parent;
			}
			else{
				if(!brother->right || brother->right->color == COLOR_BLACK)
				{
				   //3) Case 3: x's brother is COLOR_BLACK, and brother left child is COLOR_RED, 
				   // right child is COLOR_BLACK


				   brother->left->color = COLOR_BLACK;
				   brother->color = COLOR_RED;
				   rb_rotate_right(root,brother);
				   brother = parent->right;
				}

				//4) Case 4: x's brother is COLOR_BLACK, and brother's right child is COLOR_RED
				brother->color = parent->color;
				parent->color = COLOR_BLACK;
				brother->right->color = COLOR_BLACK;
				rb_rotate_left(root, parent);

				node = *root;
				break;
	
			}
				
		}
		else{
			//The right branch
			brother = parent->left;


			if(brother->color == COLOR_RED)
			{
			    //1) Case 1: x's brother is COLOR_RED
				brother->color = COLOR_BLACK;
			    parent->color = COLOR_RED;
				rb_rotate_right(root,parent);
				brother = parent->left;
			}

			if((!brother->left || brother->left->color == COLOR_BLACK) &&
				(!brother->right || brother->right->color == COLOR_BLACK))
			{
			   //2) Case 2: x's brother is COLOR_BLACK, is its two child is NULL or COLOR_BLACK
			   brother->color = COLOR_RED;
			   node = parent;
			   parent = node->parent;
			}
			else{
				if(!brother->left || brother->left->color == COLOR_BLACK)
				{
				   //3) Case 3: x's brother is COLOR_BLACK, and brother right child is COLOR_RED, 
				   // left child is COLOR_BLACK


				   brother->right->color = COLOR_BLACK;
				   brother->color = COLOR_RED;
				   rb_rotate_left(root,brother);
				   brother = parent->left;
				}

				//4) Case 4: x's brother is COLOR_BLACK, and brother's left child is COLOR_RED
				brother->color = parent->color;
				parent->color = COLOR_BLACK;
				brother->left->color = COLOR_BLACK;
				rb_rotate_right(root, parent);

				node = *root;
				break;
			}
		}
	}


	if(node)
	{
	    node->color = COLOR_BLACK;
	}
	return 0x0;

}

5. 红黑树操作的时间复杂度

红黑树插入需要O(log(n))次，对插入节点后的调整所做的旋转操作不会超过2次（注：这里是2次是指单次回溯），删除节点后的调整所做的旋转操作不会超过3次（注：这里3次是指单次回溯），沿树回溯至多O(log(n))次。总而言之，红黑树插入和删除的时间复杂度均为O(log(n))。

[参看]:

Ivanzz

发上等愿，结中等缘，享下等福；择高处立，寻平处住，向宽处行