外部排序之败者树

本节主要介绍一些败者树及其使用场景，然后给出一个败者树的实现。

1. 败者树介绍

败者树是树形选择排序的一种变形，主要会用于外部多路归并排序。在大部分情况下我们接触到的都是胜者树, 即每个非终端节点均表示其左、右孩子节点中的胜者。反之，如果在双亲节点中记下刚进行完的这场比赛中的败者，而让胜者去参加更高一层的比赛，便可得到一棵败者树。

如下图(a)所示为一棵5-路归并的败者树ls[0..4]，图中方形节点表示叶子节点（也可看成是外节点），分别为5个归并段中当前参加归并选择的记录的关键字；败者树中根节点ls[1]的双亲节点ls[0]为“冠军”，在此指示各归并段中的最小关键字记录为第三段中的当前记录；节点ls[3]指示 b1 和 b2 两个叶子节点中的败者即b2，而胜者b1和b3(b3是叶子节点b3、b4和b0经过两场比赛后选出来的获胜者）进行比较，节点ls[1]则指示它们中的败者为b1。在选得最小关键字的记录之后，只要修改叶子节点b3中的值，使其为同一归并段中的下一个记录的关键字，然后从该节点向上和双亲节点所指的关键字进行比较，败者留在该双亲节点，胜者继续向上直至树根的双亲。

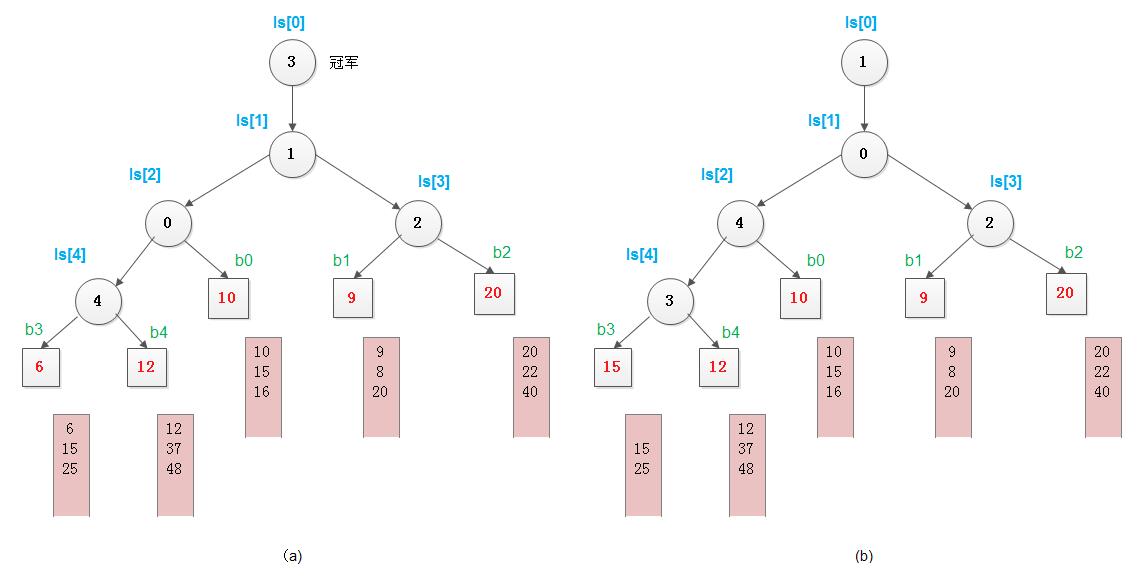
ds-loser-tree

上图(b)所示，当第3个归并段中第2个记录参加归并时，选得的最小关键字记录为第一个归并段中的记录。为了防止在归并过程中某个归并段变空，可以在每个归并段中附加一个关键字为最大值的记录。当选出“冠军”记录的关键字为最大值时，表明此次归并已经完成。由于实现k-路归并的败者树的深度为⌈log2^n⌉ + 1，则在k个记录中选择最小关键字仅需进行⌈log2^n⌉次比较。败者树的初始化也容易实现，只要先令所有的非终端节点指向一个含最小关键字的叶子节点，然后从各个叶子节点出发调整非终端节点为新的败者即可。

下面的算法11.1简单描述利用败者树进行k-路归并的过程。为了突出如何利用败者树进行归并，在算法中避开了外存信息存取的细节，可以认为归并段已在内存。算法11.2描述在从败者树选得最小关键字的记录之后，如何从叶到根调整败者树选得下一个最小关键字。算法11.3为初建败者树的过程的算法描述：

算法11.1

typedef int LoserTree[k];      //败者树是完全二叉树且不含叶子，可采用顺序存储结构

typedef struct{

	KeyType key;
	
}ExNode, External[k+1];        //外结点，只存放待归并记录的关键字



void K_Merge(LoserTree &ls, External &b)
{
	//利用败者树将编号从0到k-1的k个输入归并段中的记录归并到输出归并段
	//b[0]至b[k-1]为败者树上的k个叶子节点，分别存放k个输入归并段中当前记录的关键字
	
	for(i = 0; i<k; i++)
		input(b[i].key);       //分别从k个输入归并段读入该段当前第一个记录的关键字到外节点
		
		
	CreateLoserTree(ls);       //建败者树ls，选得最小关键字为b[ls[0]].key
	
	
	while(b[ls[0]].key != MAXKEY)
	{
		q = ls[0];             //q指示当前最小关键字所在的归并段
		
		output(q);             //将编号为q的归并段中当前(关键字为b[q].key)的记录写至输出归并段
		
		input(b[q].key, q);    //从编号为q的输入归并段中读入下一个记录的关键字
		
		Adjust(ls, q);         //调整败者树，选择新的最小关键字
	
	}
	
	output(ls[0]);             //将含最大关键字MAXKEY的记录写至输出归并段
}

算法11.2

void Adjust(LoserTree &ls, int s)
{
	//沿从叶子节点b[s]到根节点ls[0]的路径调整败者树
	
	t = (s + k) / 2;          //ls[t]是b[s]的双亲节点
	
	while(t > 0){
		if (b[s].key > b[ls[t]].key)
			s <-> ls[t];             //s指示新的胜者
			
		t = t / 2;		
	}
	
	ls[0] = s;
}

算法11.3

void CreateLoserTree(LoserTree &ls)
{
	//已知b[0]到b[k-1]为完全二叉树ls的叶子节点存有k个关键字，沿从叶子
	//到根的k条路径将ls调整为败者树
	
	b[k] = MINKEY;           //设MINKEY为关键字可能的最小值
	
	for(i = 0; i<k; i++)
		ls[i] = k;           //设置ls中“败者”的初值
		
	for(i = k-1; i>=0; i--)
		Adjust(ls, i);       //依次从b[k-1], b[k-2], ... , b[0]出发调整败者树
}

最后要提及一点，k值的选择并非越大越好，如何选择合适的k是一个需要综合考虑的问题。

2. 败者树实现

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
#include <vector>

typedef int ElemType;

typedef struct MSegment{
	ElemType *base;
	int size;
	
	int offset;
}m_segment_t;

typedef struct loster_tree_s{
	int k;
	
	int *losers;               //losers[i]为-1，表示绝对最小值; losers[i]为-2，表示绝对最大值 
	m_segment_t *segments;
}loser_tree_t;


loser_tree_t * create_loser_tree(int k)
{
	if(k <= 1)
		return NULL;
		
	loser_tree_t *root = (loser_tree_t *)malloc(sizeof(loser_tree_t));
	if(root){
		root->k = k;
		
		root->losers = (int *)malloc(sizeof(int) * k);
		root->segments = (m_segment_t *)malloc(sizeof(m_segment_t) * k);
		
		if(!root->losers || !root->segments){
			free(root->losers);
			free(root->segments);
			free(root);
			return NULL;
		}
		
		memset(root->losers, 0x0, sizeof(int)*k);
		memset(root->segments, 0x0, sizeof(m_segment_t)*k);
		
		return root;
	}
	
	
	return root;
		
}

void print_loser_tree(loser_tree_t *root)
{
	
	for(int i= 0;i<root->k;i++){
		printf("第%d个归并段：", i);
		
		for(int j=0;j<root->segments[i].size;j++)
			printf("%d ", root->segments[i].base[j]);
		printf("\n");
		
	}
	
}

void adjust(loser_tree_t *root, int s)
{
	
	//adjust the loser-tree from the leafs to the root
	int t = (root->k + s) >> 1;   //losers[t] is the parent of s
	
	
	int nexts = s;
	
	if(root->segments[s].offset >= root->segments[s].size)
		nexts = -2;
	
	while(t > 0){
		
		if(root->losers[t] == -1){
			root->losers[t] = nexts;
			nexts = -1;
		}
		else if(nexts == -2){
			
			nexts = root->losers[t];
			root->losers[t] = -2;
		}
		else if(root->losers[t] == -2 || nexts == -1)
		{
			//do nothing
		}
		else{
			ElemType e = *(root->segments[nexts].base + root->segments[nexts].offset);
			ElemType f = *(root->segments[root->losers[t]].base + root->segments[root->losers[t]].offset);
		
			if(e > f){
				int curLoser = nexts;
				nexts = root->losers[t];
				root->losers[t] = curLoser;
			}
		}
		
		t = t>>1;
	}
	
	root->losers[t] = nexts;
}


int init_loser_tree(loser_tree_t *root)
{
	
	for(int i = 0;i<root->k;i++)
		root->losers[i] = -1;
	
	printf("将创建%d个归并段，每个归并段中以从小到大顺序输入若干元素(元素与元素之间以空格分割)\n", root->k);
	for(int i=0;i<root->k;i++){
		
		char buf[2048] = {0};
		char *p = buf;
		char *end;
		std::vector<long> vec;
		long num;
		
		printf("请输入第 %d 个归并段元素(元素之间以空格分割): ", i);
		fgets(p, 2048, stdin);
		
		while(num = strtol(p, &end, 10)){
			vec.push_back(num);
			p = end+1;
		}
		
		if(vec.size() > 0){
				root->segments[i].size = vec.size();
				root->segments[i].base = (ElemType *)malloc(sizeof(ElemType) * vec.size());
				if(!root->segments[i].base){
					printf("初始化归并段 %d 失败\n", i);
					return -1;
				}
				
				for(int j= 0;j<vec.size();j++)
					root->segments[i].base[j] = (int)vec[j];
		}
		
	}
	
	printf("\n");
	printf("=====输出我们创建的归并段=====\n");
	print_loser_tree(root);
	printf("\n");
	
	for(int i = root->k-1;i>=0;i--){
		adjust(root, i);
	}
	
	
	return 0x0;
}

void multiways_merge(loser_tree_t *root)
{
	
	while(root->losers[0] != -2){
		int s = root->losers[0];
		if(s == -1){
			printf("skip definitly minimum\n");
			continue;
		}
		
		printf("%d ", *(root->segments[s].base + root->segments[s].offset));
		root->segments[s].offset++;
		
		adjust(root, s);
	}
	printf("\n");
}

int main(int argc, char *argv[])
{
	loser_tree_t *root = NULL;
	
	root = create_loser_tree(5);
	init_loser_tree(root);
	
	multiways_merge(root);
	
	return 0x0;
}

编译运行：

# gcc -o loser_tree loser_tree.cpp -lstdc++
# ./loser_tree 
将创建5个归并段，每个归并段中以从小到大顺序输入若干元素(元素与元素之间以空格分割)
请输入第 0 个归并段元素(元素之间以空格分割): 
请输入第 1 个归并段元素(元素之间以空格分割): 3 20
请输入第 2 个归并段元素(元素之间以空格分割): 4 
请输入第 3 个归并段元素(元素之间以空格分割): 50
请输入第 4 个归并段元素(元素之间以空格分割): 201

=====输出我们创建的归并段=====
第0个归并段：
第1个归并段：3 20 
第2个归并段：4 
第3个归并段：50 
第4个归并段：201 

3 4 20 50 201

[参看]:

Ivanzz

发上等愿，结中等缘，享下等福；择高处立，寻平处住，向宽处行

外部排序之败者树

1. 败者树介绍

2. 败者树实现