本文我们主要讲述一下键树的原理及相应实现。

1. 键树

键树又称为数字查找树(Digital Search Tree)。它是一棵度>=2的树，树中的每个节点中不是包含一个或几个关键字，而是只包含组成关键字的符号。例如，若关键字是数值，则节点中只包含一个数位；若关键字是单词，则节点中只包含一个字母字符。这种树会给某种类型关键字的表的查找带来方便。

假设有如下16个关键字的集合：

{
	CAI、CAO、LI、LAN、CHA、CHANG、WEN、CHAO、YUN、YANG、LONG、WANG、ZHAO、LIU、WU、CHEN
}

可对此集合作如下的逐层分割。首先按其首字符将它们分成5个子集：

{CAI、CAO、CHA、CHANG、ChAO、CHEN},
{WEN、WANG、WU},
{ZHAO},
{LI、LAN、LONG、LIU},
{YUN, YANG}

然后对其中4个关键字个数大于1的子集再按第二个字符不同进行分割。若所得子集的关键字多于1个，则还需按其第三个字符不同进行分割。以此类推，直至每个小子集中只包含一个关键字为止。例如对首字符为C的集合可进行如下的分割：

{
  {(CAI)、(CAO)},
  {
    {(CHA)、(CHANG)、(CHAO)},
    (CHEN)
  }
}

显然，如此集合、子集和元素之间的层次关系可以用一棵树来表示，这棵树便为键树。例如，上述集合及其分割可用图9.19所示的键树来表示。树中根节点的五棵子树分别表示：

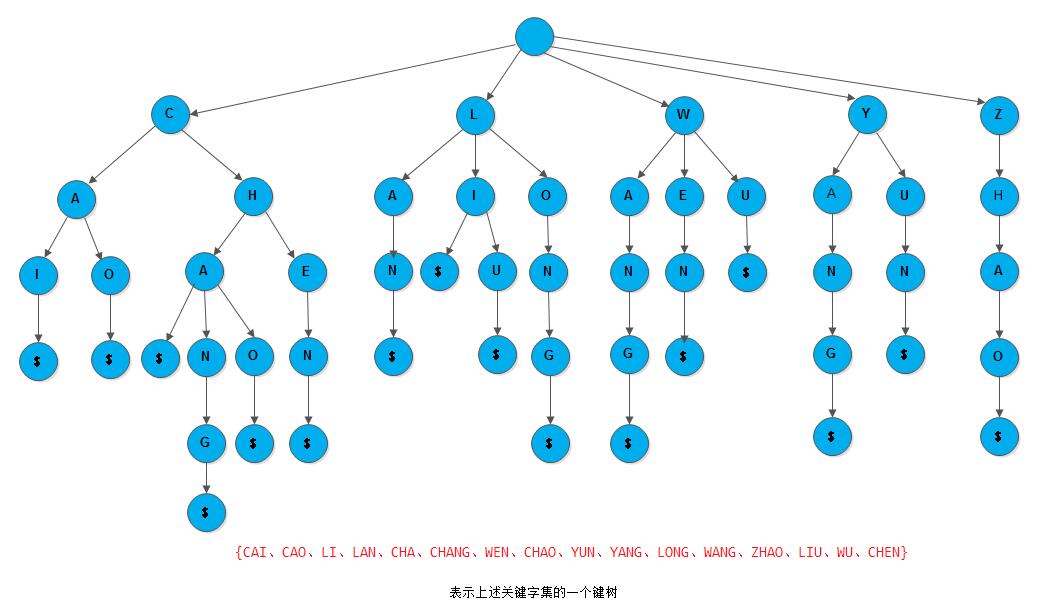
树中根节点的5棵子树分别表示首字符为C、L、W、Y和Z的5个关键字子集。从根到叶子节点路径中节点的字符组成的字符串表示一个关键字， 叶子节点中的特殊符号表示字符串的结束。在叶子节点还含有指向该关键字记录的指针。

为了查找和插入方便，我们约定键树是有序树，即同一层中兄弟节点之间依所含符号自左至右有序，并约定结束符$小于任何字符。

2. 键树的存储结构

通常，键树有两种存储结构，下面分别进行讲述。

2.1 双链树结构

此种数据结构通常用左孩子，右兄弟链表来表示键树，则每个分支节点包括3个域：

• symbol域： 存储关键字的一个字符；

• first域： 存储指向第一棵子树根的指针；

• next域: 存储指向右兄弟的指针；

同时，叶子节点的infoptr域存储指向该关键字记录的指针。此时的键树又称双链树。上图所示的双链树如下图所示（图中只画出了第一棵子树，其余部分省略)：

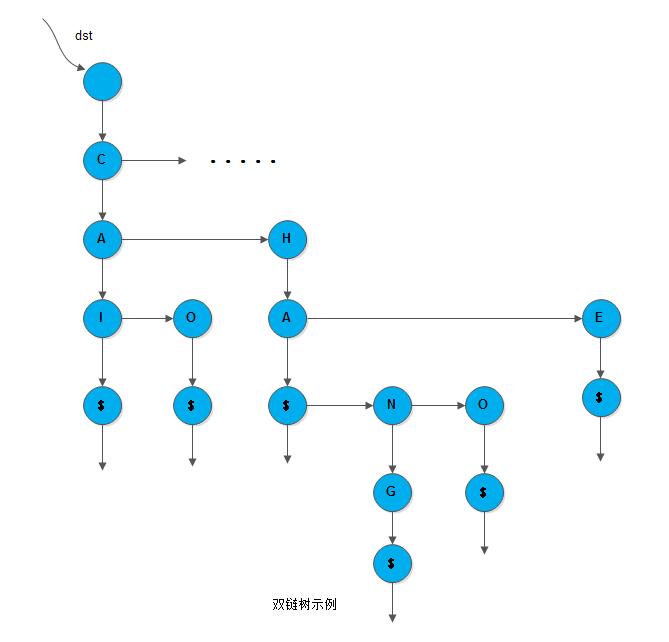
双链树的查找可如下进行：假设给定值为K.ch(0..num-1)，其中K.ch[0]至K.ch[num-2]表示待查关键字中num-1个字符，K.ch[num-1]为结束符$，从双链树的根指针出发，顺first指针找到第一棵子树的根节点，以K.ch[0]和此节点的symbol域比较，若相等，则顺first域再比较下一字符，否则沿next域顺序查找。若直至空仍比较不等，则查找不成功。

1) 双链树存储结构

如果采用双链树来存储键树，则类似于如下：

//The keyword max length
#define MAXKEYLEN	16



typedef struct{
	char ch[MAXKEYLEN];		//the keyword
	int num;				//the keyword length
}KeysType;

typedef enum{LEAF, BRANCH} NodeKind;     


//double link tree node
typedef struct DLTNode{
	char symbol;

	struct DLTNode *next;     //point to  the brother
	NodeKind kind;

	union{
		Record *infoptr;      //the leaf node which point to the record
		struct DLTNode *first;  //the branch node which point to its child
	};
}DLTNode, *DLTree;

2) 双链树的查找

针对如上结构，在双链树中进行查找类似于如下：

//Search in NONE NULL double link tree
Record * SearchDLTree(DLTree T, KeysType K)
{
	DLTNode *p = T->first;
	i = 0;

	while(p && i < K.num)
	{
		//find the keyword[i]
		while(p && p->symbol != K.ch[i]) p = p->next;

		if(p && i<K.num-1) p = p->first;

		++i;
	}

	if(!p)	return NULL;
	else
		return p->infoptr;
	
	
}

键树中每个节点的最大度d和关键字的“基”有关。若关键字是单词，则d=27; 若关键字是数值，则d=11。键树的深度取决于关键字中字符或数位的个数。假设关键字为随机的（即关键字中每一位取基内任何值的概率相同），则在双链树中查找每一位的平均查找长度为(1+d)/2。又假设关键字中字符（或数位）的个数都相等，则在双链树中进行查找的平均查找长度为h*(1+d)/2。

在双链树中插入或删除一个关键字，相当于在树中某个节点上插入或删除一棵子树，再此不再详述。

2.2 Trie树

若以树的多重链表表示键树，则树的每个节点中应含有d个指针域，此时的键树又称Trie树。若从键树中某个节点到叶子节点的路径上每个节点都只有一个孩子，则可将该路径上的所有节点压缩成一个"叶子节点"，且在该叶子节点中存储关键字及指向记录的指针等信息。例如，在ds-ds-tree所示的键树中，从节点Z到节点$为单支树，则在下图所示相应的Trie树中只有一个含关键字ZHAO及相关信息的叶子节点。由此，在Trie树中有两种节点：

• 分支节点： 含有d个指针域和一个指示该节点中非空指针域的个数的整数域

• 叶子节点: 含有关键字域和指向记录的指针域

在分支节点中不设数据域，每个分支节点所表示的字符均由其双亲节点中（指向该节点）的指针位置所决定。

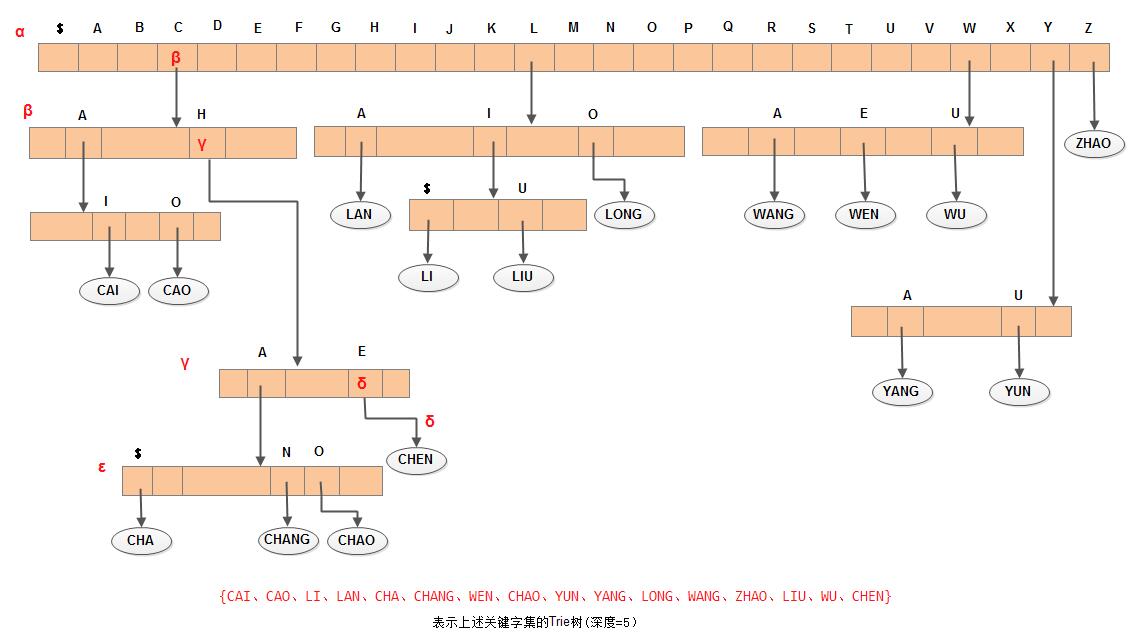
在Trie树上进行查找的过程为：从根节点出发，沿和给定值相应的指针逐层向下，直至叶子节点， 若叶子节点中的关键字和给定值相等，则查找成功；若分支节点中和给定值相应的指针为空，或叶节点中的关键字和给定值不相等，则查找不成功。

trie这个词是从retrieve(检索）中取中间4个字符而构成，读音同(try)

1）Trie树存储结构

//The keyword max length
#define MAXKEYLEN	16



typedef struct{
	char ch[MAXKEYLEN];		//the keyword
	int num;				//the keyword length
}KeysType;

typedef enum{LEAF, BRANCH} NodeKind;     

//Trie Tree 
typedef struct TrieNode{
	NodeKind kind;

	union{
		//leaf node
		struct LeafNode{
			KeysType K,
			Record *infoptr;
		}lf;      

		//branch node
		struct BranchNode{
			struct TrieNode *ptr[27];
			int num;
		}bh;
	};
}TrieNode, *TrieTree;

2）Trie树的查找

针对上述结构，Trie树的查找类似于如下：

Record *SearchTrie(TrieTree T, KeysType K)
{
	TrieNode *p;
	int i;

	//Note: 'ord' function is used to calc the order of ch[i] in alphabet
	for(p = T, i = 0; p && p->kind == BRANCH && i<K.num;
		p = p->bh.ptr[ord(K.ch[i])], ++i);

	if(p && p->kind == LEAF && p->lf.K == K) 
		return p->lf.infoptr;
	else
		return NULL;
}

从上述查找过程可见，在查找成功时走了一条从根到叶子节点的路径。例如，在上图中查找CHEN的过程为： 从根节点α出发，经β、γ节点，最后到达叶子节点δ。而查找CHAI的过程为从根节点α出发，经β、γ节点后到达ε节点, 由于该节点中和字符I相应为空，则查找不成功。由此，其查找的时间依赖于树的深度。我们可以对关键字选择一种合适的分割，以缩减Trie树的深度。例如下面的关键字：

{
    CAI、CAO、LI、LAN、CHA、CHANG、WEN、CHAO、YUN、YANG、LONG、WANG、ZHAO、LIU、WU、CHEN
}

根据关键字集的特点，可作如下分割。先按首字符不同分成多个子集之后，然后按最后一个字符不同分割每个子集，再按第二个字符…，前后交叉分割。由此，得到如下所示的Trie树:

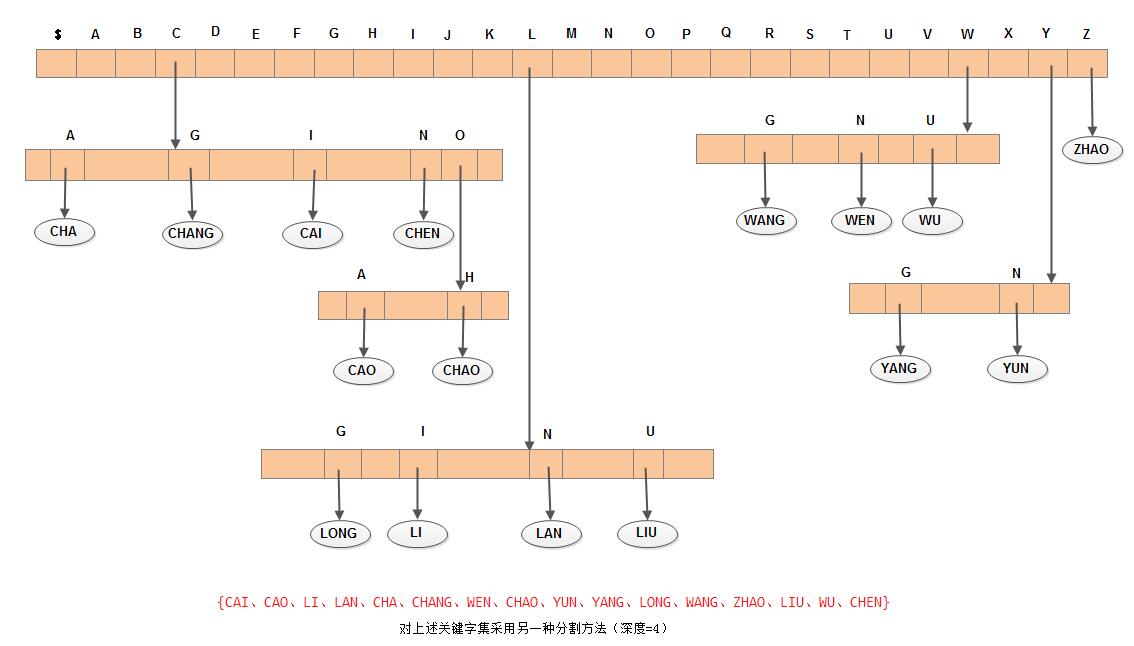
在该树上，除两个叶子节点在第四层上外，其余叶子节点均在第三层上。还可限制Trie树的深度。假设允许Trie树的最大深度为L，则所有直至L-1层皆为同义词的关键字都进入同一叶子节点。若分割得合适，则可使每个叶子节点中只含有少数几个同义词。当然也可增加分支的个数以减少树的深度。

在Trie树上易于进行插入和删除，只是需要相应地增加和删除一些分支节点。当分支节点中num域的值减为1时，便可被删除。

3. 总结

双链树和Trie树是键树的两种不同的表示方法，他们有各自的特点。从其不同的存储结构特性可见，若键树中节点的度较大，则采用Trie树结构较双链树更为合适。

综上对树表的讨论可见，它们的查找过程都是从根节点出发，走了一条从根到叶子（或非终端节点）的路径，其查找时间依赖于树的深度。由于树表主要用作文件索引，因此节点的存取还涉及外部存储设备的特性，故在此没有对它们作平均查找长度的分析。