图（Graph)是一种较线性表和树更为复杂的数据结构。在线性表中，数据元素之间仅有线性关系，每个数据元素只有一个直接前驱和一个直接后继；在树形结构中，数据元素之间有着明显的层次关系，并且每一层上的数据元素可能和下一层中多个元素（即其孩子节点）相关，但只能和上一层中一个元素（即其双亲节点）相关；而在图形结构中，节点之间的关系可以是任意的，图中任意两个数据元素之间都可能相关。由此，图的应用极为广泛，特别是近年来的迅速发展，已渗入到诸如语言学、逻辑学、物理、化学、电讯工程、计算机科学以及数学的其他分支中。

1. 图的定义和术语

图是一种数据结构，加上一组基本操作，就构成了抽象数据类型。抽象数据类型图的定义如下：

ADT Graph{
    数据对象V： V是具有相同特性的数据元素的集合，称为顶点集。
    数据关系R: 
          R={VR}
          VR={<v,w>|v,w∈V 且P(v,w), <v,w>表示从v到w的弧
              谓词P(v,w)定义了弧<v,w>的意义或信息}

    基本操作P：
        CreateGraph(&G, V, VR);
           初始条件： V是图的顶点集，VR是图中弧的集合
           操作结果： 按V和VR的定义构造图；

        DestroyGraph(&G);
           初始条件： 图G存在
           操作结果： 销毁图G  

        LocateVex(G, u);
           初始条件： 图G存在，u和G中顶点有相同特征。
           操作结果： 若G中存在顶点u，则返回该顶点在图中的位置；否则返回其他信息。

        GetVex(G, v);
           初始条件： 图G存在，v是G中某个顶点。
           操作结果： 返回v的值

        PutVex(&G, v, value);
           初始条件： 图G存在，v是G中某个顶点
           操作结果： 对v赋值value

        FirstAdjVex(G, v);
           初始条件： 图G存在，v是G中某个顶点。
           操作结果： 返回v的第一个邻接顶点。若顶点在G中没有邻接顶点，则返回“空”

        NextAdjVex(G, v, w);
           初始条件： 图G存在，v是G中某个顶点，w是v的邻接顶点。
           操作结果： 返回v的（相对于w的）下一个邻接顶点。若w是v的最后一个邻接点，则返回“空”

        InsertVex(&G, v);
           初始条件： 图G存在，v和图中顶点有相同特征。
           操作结果： 在图中增加新顶点v

        DeleteVex(&G, v);
           初始条件： 图G存在，v是G中某个顶点。
           操作结果： 删除G中顶点v及其相关的弧

        InsertArc(&G, v, w);
           初始条件： 图G存在，v和w是G中两个顶点。
           操作结果： 在G中添加弧<v,w>，若G是无向的，则还增加对称弧<w,v>

        DeleteArc(&G, v,w);
           初始条件： 图G存在，v和w是G中两个顶点
           操作结果： 在G中删除弧<v,w>，若G是无向的，则还删除对称弧<w,v>

        DFSTraverse(G, Visit());
           初始条件： 图G存在，Visit()是顶点的应用函数
           操作结果： 对图进行深度优先遍历。在遍历过程中，对每个顶点调用函数Visit()一次且仅一次。一旦Visit()失败，则操作失败

        BFSTraverse(G, Visit());
           初始条件： 图G存在，Visit()是顶点的应用函数
           操作结果： 对图进行广度优先遍历。在遍历过程中，对每个顶点调用函数Visit()一次且仅一次。一旦Visit()失败，则操作失败
}ADT Graph

在图中的数据元素通常称作顶点(Vertex)， V是顶点的有穷非空集合； VR是两个顶点之间的关系的集合。若<v,w>∈VR，则<v,w>表示从v到w的一条弧(Arc)，且称v为弧尾(Tail)或初始点(Initial node)，成w为弧头(Head)或终端点（Terminal node)，此时的图称为有向图(Digraph)。若<v,w>∈VR必有<w,v>∈VR，即VR是对称的，则以无序对(v,w）代替这两个有序对，表示v和w之间的一条边(Edge)，此时的图称为无向图(Undigraph)。

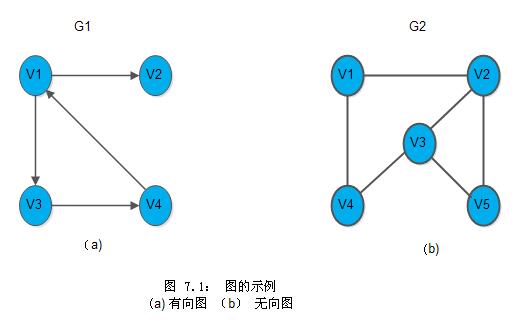
如上图(a)中G1是有向图，定义此图的谓词P(v,w)则表示从v到w的一条单向通路：

G1 = (V1, {A1})

其中：
V1={v1,v2,v3,v4}
A1={<v1,v2>, <v1,v3>, <v3,v4>, <v4,v1>}

上图(b)中G2为无向图：

G2=(V2, {E2})

其中：
V2={v1,v2,v3,v4,v5}
E2={(v1,v2), (v1,v4), (v2,v3), (v2,v5), (v3,v4), (v3,v5)}

我们用 n 表示图中顶点数目，用 e 表示边或弧的数目。在下面的讨论中，我们不考虑顶点到其自身的弧或边，即若<vi,vj>∈VR，则vi≠vj，那么，对于无向图， e的取值范围是 0 到 n(n-1)/2。有n(n-1)/2条边的无向图称为完全图(Completed Graph)。对于有向图，e的取值范围是 0 到 n(n-1)。具有n(n-1)的有向图称为有向完全图。有很少边或弧（如 e<nlogn)的图称为稀疏图(Sparse Graph)，反之称为稠密图(Dense Graph)。

有时图的边或弧具有与它相关的数，这种与图的边或弧相关的数叫做权（Weight)。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图称为网(Network)。

说明： 所谓网络就是边上有权值的图
      无向网就是边上有权值的无向图，一般而言，无向图重点在于无向，有无权值不定

假设有两个图G=(V, {E})和G'=(V', {E'})，如果V’⊆V且E’⊆E，则称G’为G的子图(Subgraph)。例如，下面就是子图的例子：

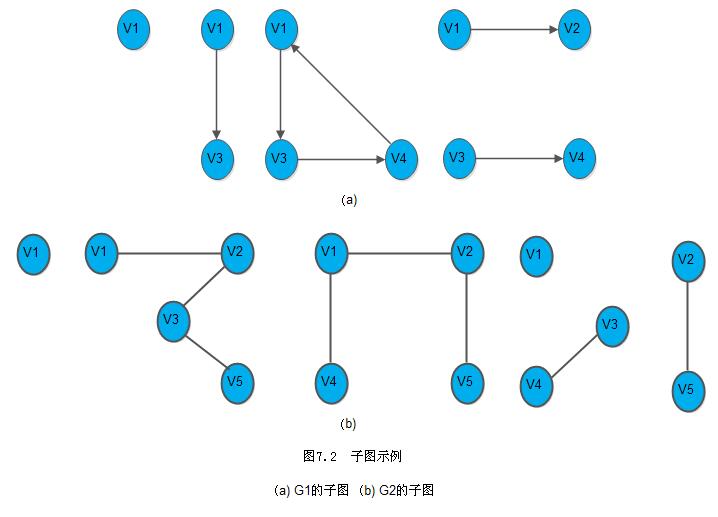
对于无向图G=(V,{E})，如果边(v,v')∈E，则称顶点v和v’互为邻接点（Adjacent)，即v和v’相邻接。边(v,v')依附(Incident)依附于顶点v和v’，或者说(v，v’)和顶点v与v’相关联。顶点v的度(Degree)是和v相关联的边的数目，记为TD(V)。例如，G2中顶点V3的度是3。

对于有向图G=(V, {A})，如果弧<v,v'>∈A，则称顶点v邻接到顶点v'，顶点v'邻接自v。弧<v,v'>和顶点v、v'相关联。以顶点v为头的弧的数目称为v的入度(InDegree)，记为ID(v)； 以v为尾的弧的数目称为v的出度(OutDegree)，记为OD(v)；顶点v的度为TD(v)=ID(v) + OD(v)。例如，图G1中顶点v1的入度ID(v1)=1，出度OD(v1)=2，度TD(v1)=ID(v1)+OD(v1)=3。一般地，如果顶点vi的度记为TD(vi)，那么一个有n个顶点，e条边或弧的图，满足如下关系：

无向图G=(V, {E})中从顶点v到顶点v'的路径(Path)是一个顶点序列：$(v=v_{i,0},v_{i,1}, …, v_{i,m}=v’)$，其中$(v_{i, j-1}, v_{i, j}) \in E, 1 \leq i \leq m$。

如果G是有向图，则路径也是有向的，顶点序列应满足：$<v_{i, j-1}, v_{i,j}> \in E, 1 \leq i \leq m$。路径的长度是路径上的边或弧的数目。第一个顶点和最后一个顶点相同的路径称为回路或环(Cycle)。序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。

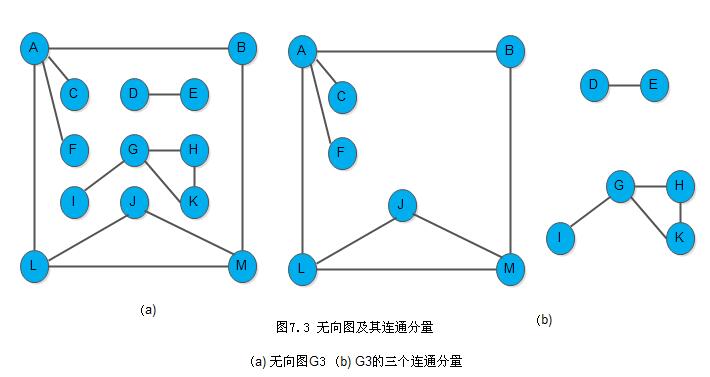
在无向图G中，如果从顶点v到顶点v'有路径，则称v和v’是连通的。如果对于图中任意两个顶点vi、vj∈V，$v_i$和$v_j$都是连通的，则称G是连通图(Connected Graph)。图7.1(b)中的G2就是一个连通图，而图7.3(a)中G3则是非连通图，但G3有3个连通分量，如图7.3(b)所示。所谓连通分量（Connected Component)，指的是无向图中的极大连通子图。

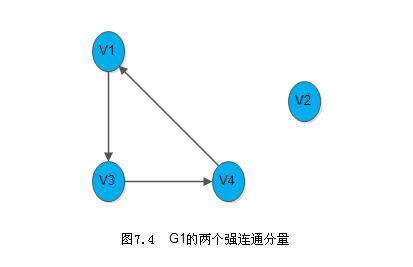
在有向图G中，如果对于每一对$\bbox[yellow,10px]{v_i,v_j \in V，vi \neq vj}$，从$v_i$到$v_j$和从$v_j$到$v_i$都存在路径，则称G是强连通图。有向图中的极大强连通子图称作有向图的强连通分量。例如7.1(a)中的G1不是强连通图，但它两个强连通分量，如下图7.4所示：

一个连通图的生成树是一个极小连通子图，它含有图中全部顶点，但只有足以构成一棵树的(n-1)条边。图7.5是G3中最大连通分量的一棵生成树。如果在一棵生成树上添加一条边，必定构成一个环，因为这条边使得它依附的那两个顶点之间有了第二条路径。

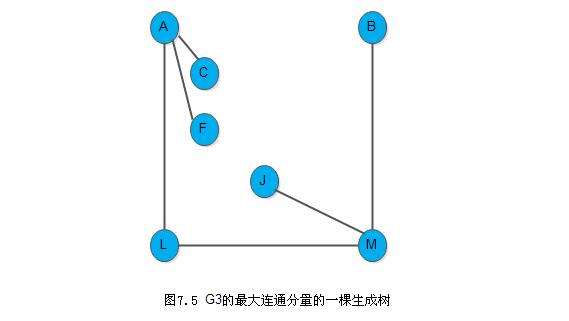
一棵有n个顶点的生成树有且仅有n-1条边。如果一个图有n个顶点和小于n-1条边，则是非连通图。如果多余n-1条边，则一定有环。但是，有n-1条边的图不一定是生成树。

如果一个有向图恰有一个顶点的入度为0，其余顶点的入度均为1，则是一棵有向树。一个有向图的生成森林由若干棵有向树组成，含有图中全部顶点，但只有足以构成若干棵不相交的有向树的弧。图7.6所示为其一例：

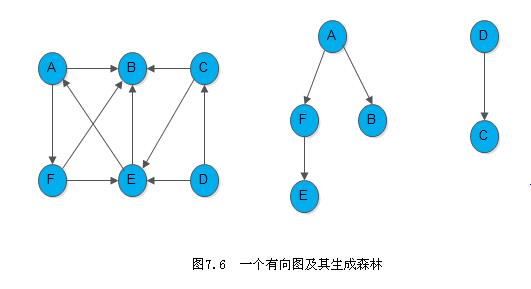
在前述图的基本操作的定义中，关于 “顶点的位置” 和 “邻接点的位置” 只是一个相对的概念。因为，从图的逻辑结构的定义来看，图中的顶点之间不存在全序的关系（即无法将图中顶点排列成一个线性序列），任何一个顶点都可被看成是第一个顶点；另一方面，任一顶点的邻接点之间也不存在次序关系。但为了操作方便，我们需要将图中顶点按任意的顺序排列起来（这个排列和关系VR无关）。由此，所谓 “顶点在图中的位置” 指的是该顶点在这个人为的随意排列中的位置（或序号）。同理，可对某个顶点的所有邻接点进行排队，在这个排队中自然形成了第一个或第 k 个邻接点。若某个顶点的邻接点的个数大于k，则称第 k+1 个邻接点为第 k 个邻接点的下一个邻接点，而最后一个邻接点的下一个邻接点为“空”。

2. 图的存储结构

在前面几章讨论的数据结构中，除了广义表和树以外，都可以有两类不同的存储结构，它们是由不同的映像方法（顺序映像和链式映像）得到的。由于图的结构比较复杂，任意两个顶点之间都可能存在联系，因此无法以数据元素在存储区中的物理位置来表示元素之间的关系，即图没有顺序映像的存储结构，但可以借助数组的数据类型表示元素之间的关系。另一方面，用多重链表表示图是自然的事，它是一种最简单的链式映像结构，即以一个由数据域和多个指针域组成的节点表示图中一个顶点，其中数据域存储该顶点的信息，指针域存储指向其邻接点的指针，如图下图7.7所示为图7.1中有向图G1和无向图G2的多重链表：

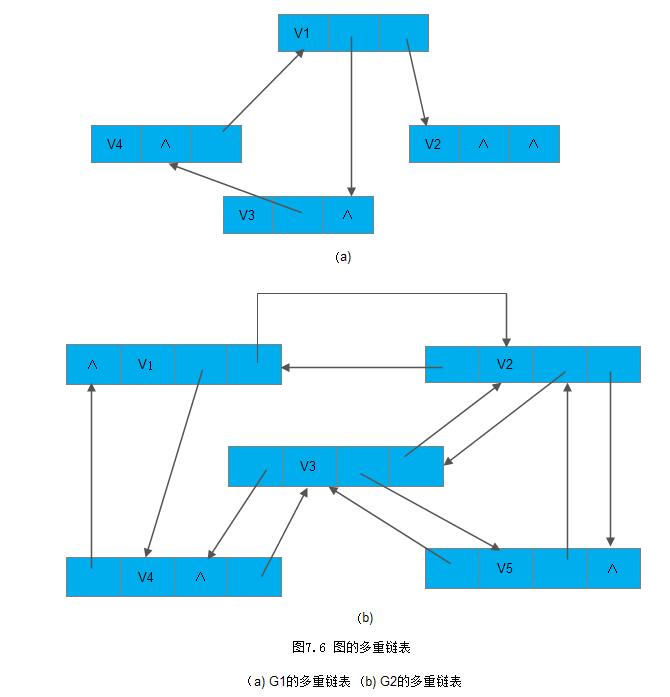
但是，由于图中各个结点的度数各不相同，最大度数和最小度数可能相差很多，因此，若按度数最大的顶点设计节点结构，则会浪费很多存储单元； 反之，若按每个顶点自己的度数设计不同的结点结构，又会给操作带来不便。因此，和树类似，在实际应用中不宜采用这种结构，而应根据具体的图和需要进行的操作，设计恰当的节点结构和表结构。常用的有邻接表、邻接多重表和十字链表。下面分别讨论。

2.1 数组表示法

用两个数组分别存储数据元素（顶点）的信息和数据元素之间的关系（边或弧）的信息。其形式描述如下：

//------------图的数组（邻接矩阵）存储表示--------------------

#define INFINITY INT_MAX           //最大值∞(无穷）
#define MAX_VERTEX_NUM 20          //最大顶点个数

typedef enum{DG, DN, UDG, UDN} GraphKind;  //{有向图，有向网， 无向图， 无向网}

typedef struct ArcCell{
   VRType adj;      //VRType是顶点关系类型。对无权图，用1或0表示相邻否； 对带权图，则为权值类型
   
   InfoType *info;  //该弧相关信息的指针
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

typedef struct{
    VertexType vexs[MAX_VERTEX_NUM];      //顶点向量
    AdjMatrix arcs;                       //邻接矩阵
    int vexnum, arcnum;                   //图的当前顶点数和弧数
    GraphKind kind;                       //图的种类标志
}MGraph;

例如，图7.1中G1和G2的邻接矩阵如下图7.8所示。以二维数组表示有n个顶点的图时，需存放 n 个顶点信息和 n^2 个弧信息的存储量。若考虑无向图的邻接矩阵的对称性，则可采用压缩存储的方式只存入矩阵的下三角（或上三角）元素。

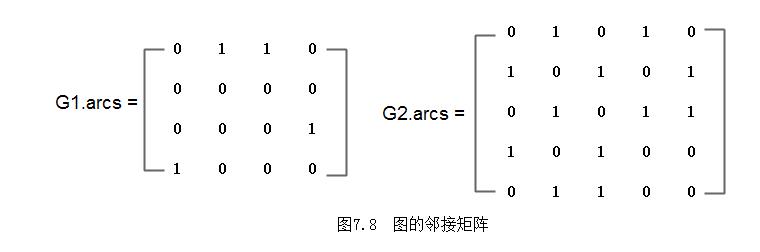
借助于邻接矩阵容易判定任意两个顶点之间是否有边（或弧）相连，并容易求得各个顶点的度。对于无向图，顶点vi的度是邻接矩阵中第i行(或第i列）的元素之和，即：

         n-1
TD(vi) = ∑A[i][j] (n=MAX_VERTEX_NUM)
         j=0

对于有向图，第i行的元素之和为顶点vi的出度OD(vi)； 第j列的元素之和为顶点vj的入度ID(vj)。

网的邻接矩阵可定义为：

例如，图7.9列出了一个有向网和它的邻接矩阵：

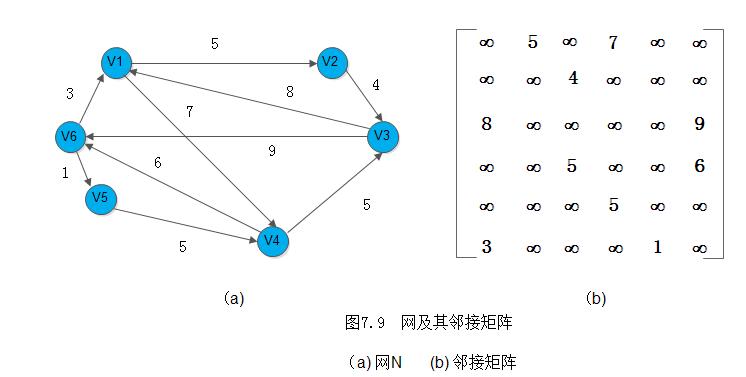
如下算法7.1是在邻接矩阵存储结构MGraph上对图的构造操作的实现框架，它根据图G的种类调用具体构造算法。如果G是无向网，则调用算法7.2。构造一个具有n个顶点和e条边的无向网 G 的时间复杂度是O(n^2 + e *n)，其中对邻接矩阵G.arcs的初始化耗费了O(n^2)的时间。

• 算法7.1

Status CreateGraph(MGraph &G){
    //采用数组（邻接矩阵）表示法，构造图G

    scanf(&G.kind);
    switch(G.kind){
        case DG: return CreateDG(G);          //构造有向图
        case DN: return CreateDN(G);          //构造有向网
        case UDG: return CreateUDG(G);        //构造无向图
        case UDN: return CreateUDN(G);        //构造无向网
        default: return ERROR;
    }
}

• 算法7.2

Status CreateUDN(MGraph &G)
{
     //采用数组（邻接矩阵）表示法，构造无向网G

    scanf(&G.vexnum, &G.arcnum, &IncInfo);      //IncInfo为0则各弧不含其他信息

    //构造顶点向量
    for(i=0;i<G.vexnum;i++)
        scanf(&G.vexs[i]);

    //初始化邻接矩阵
    for(i=0;i<G.vexnum; i++){
        for(j=0;j<G.vexnum; j++){

             G.arcs[i][j] = {INFINITY, NULL};   //{adj, info}
        }
    }

    //构造邻接矩阵
    for(i=0;i<G.arcnum; i++){
        
         scanf(&v1, &v2, &w);     //输入一条边依附的顶点及权值

         i = LocateVex(G, v1);   j= LocateVex(G, v2);    //确定v1和v2在G中的位置

         G.arcs[i][j].adj = w;          //弧<v1, v2>的权值
       
         //若弧含有相关信息，则输入
         if(IncInfo) 
             Input(*G.arcs[i][j].info);

          G.arcs[j][i] = G.arcs[i][j];    //置<v1,v2>的对称弧<v2,v1>          
    }
}

在这个存储结构上也易于本章开头所列的图的基本操作。如FirstAdjVex（G,v)找v的第一个邻接点。首先，由LocateVex(G,v)找到v在图G中的位置，即v在一维数组vexs中的序号i，则二维数组arcs中第i行上第一个adj域的值为 “1” 的分量所在的列号j，便为v的第一个邻接点在图G中的位置。同理，下一个邻接点在图G中的位置便为j列之后第一个adj域的值为 “1” 的分量所在的列号。

2.2 邻接表

邻接表(Adjacency List)是图的一种链式存储结构。在邻接表中，对图中每个顶点建立一个单链表，第i个单链表中的节点表示依附于顶点vi的边（对有向图是以顶点vi为尾的弧）。每个结点由3个域组成，其中邻接点域（adjvex)指示与顶点vi邻接的点在图中的位置；链域(nextarc)指示下一条边或弧的节点； 数据域(info)存储和边或弧相关的信息，如权值等。每个链表上附设一个表头节点。在表头节点中，除了设有链域(firstarc)指向链表中第一个节点之外，还设有存储顶点vi的名或其他信息的数据域(data)。如下图所示：

这些表头节点（可以链相接）通常以顺序结构的形式存储，以便随机访问任一顶点的链表。一个图的邻接表存储结构可形式地说明如下：

//---------------图的邻接表存储表示--------------------

#define MAX_VERTEX_NUM 20
typedef struct ArcNode{
    int adjvex;                //该弧所指向的顶点的位置
    struct ArcNode *nextarc;   //指向下一条弧的指针
    InfoType *info;            //该弧相关信息的指针
}ArcNode;

typedef struct VNode{
     VertexType data;         //顶点信息
     ArcNode *firstarc;       //指向一条依附该顶点的弧的指针
}VNode, AdjList[MAX_VERTEX_NUM];

typedef struct{
    AdjList vertices; 
    int vexnum, arcnum;       //图的当前顶点数和弧数
    int kind;                 //图的种类标志
}ALGraph;

例如下图7.10(a-2)和(b-2)所示分别为G1和G2的邻接表:

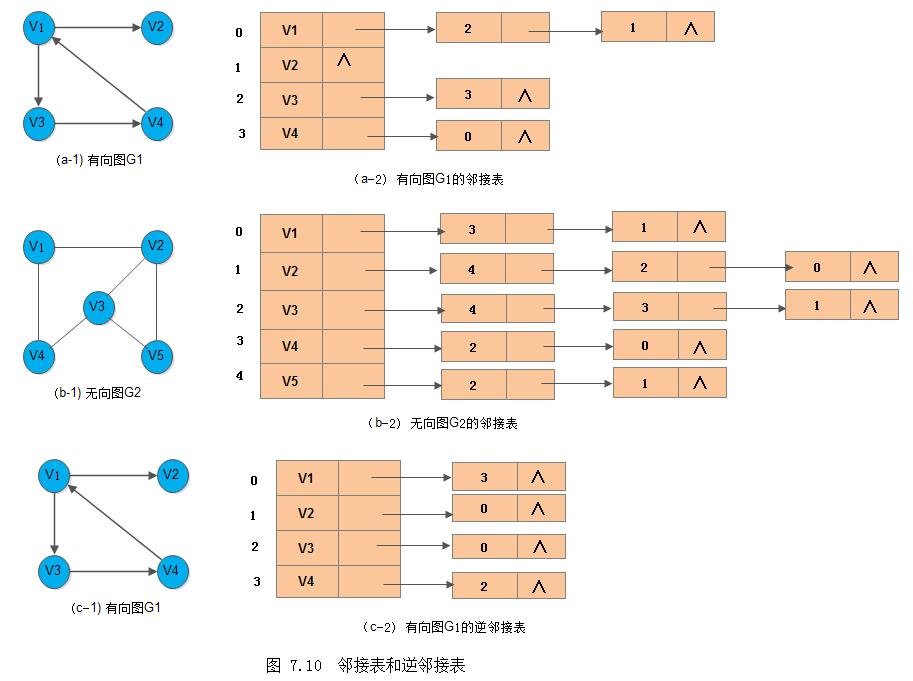
若无向图中有n个顶点、e条边，则它的邻接表需n个头节点和2e个表节点。显然，在边稀疏(e远小于n(n-1)/2，即e << n(n-1)/2)) 的情况下，用邻接表表示图比邻接矩阵节省存储空间，当和边相关的信息叫多时更是如此。

在无向图的邻接表中，顶点vi的度恰为第i个链表的节点数；而在有向图中，第i个链表中的节点个数只是顶点vi的出度，为求入度，必须遍历整个邻接表。在所有链表中其邻接点域的值为i的节点的个数是顶点vi的入度。有时，为了便于确定顶点的入度或以顶点vi与头的弧，可以建立一个有向图的逆邻接表，即对每个顶点vi建立一个链接以vi为头的弧的表，例如上图7.10(c-2)所示为7.10(c-1)中有向图G1的逆邻接表。

在建立邻接表或逆邻接表时，若输入的顶点信息即为顶点的编号，则建立邻接表的时间复杂度为O(n+e)， 否则，需要通过查找才能得到顶点在图中的位置，则时间复杂度为O(n*e)。

在邻接表上容易找到任一顶点的第一个邻接点和下一个邻接点，但要判定任意两个顶点(vi和vj)之间是否有边或弧相连，则需搜索第i个或第j个链表，因此，不及邻接矩阵方便。

2.3 十字链表

十字链表(Orthogonal List)是有向图的另一种链式存储结构。可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表。在十字链表中，对应于有向图中每一条弧有一个节点，对应于每个顶点也有一个节点。这些节点的结构如下所示：

在弧节点中有5个域： 其中尾域(tailvex)和头域(headvex)分别指示弧尾和弧头这两个顶点在图中的位置， 链域(hlink)指向弧头相同的下一条弧， 而链域(tlink)指向弧尾相同的下一条弧，info域指向该弧的相关信息。弧头相同的弧在同一链表上，弧尾相同的弧也在同一链表上。它们的头节点即为顶点节点，它由3个域组成： 其中data域存储和顶点相关的信息，如顶点的名称等； firstin和firstout为两个链域，分别指向以该顶点为弧头或弧尾的第一个弧节点。例如，图7.11(a)中所示图的十字链表如图7.11(b)所示。若将有向图的邻接矩阵看成是稀疏矩阵的话，则十字链表也可以看成是邻接矩阵的链表存储结构，在图的十字链表中，弧节点所在的链表非循环链表，节点之间相对位置自然形成，不一定按顶点序号有序，表头节点即顶点节点，它们之间不是链接，而是顺序存储。

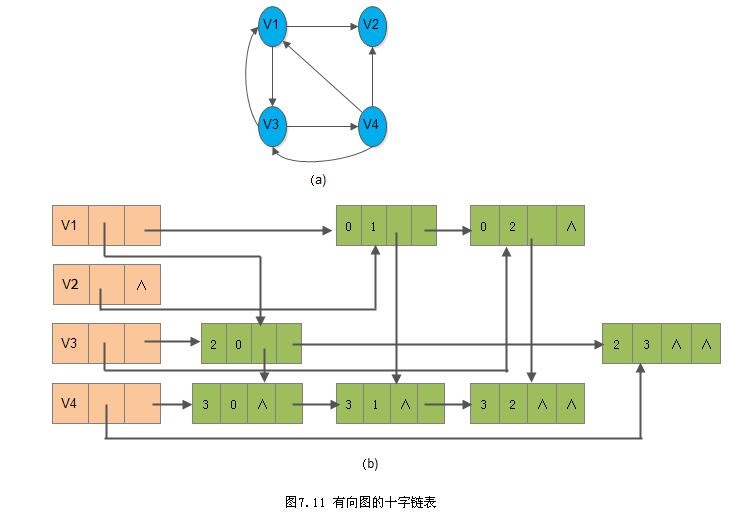
有向图的十字链表存储表示的形式说明如下所示：

//------有向图的十字链表存储表示--------

#define MAX_VERTEX_NUM 20
typedef struct ArcBox{
    int tailvex, headvex;           //该弧的尾和头顶点的位置
    struct ArcBox *hlink, *tlink;   //分别为弧头相同和弧尾相同的弧的链域
    InfoType *info;                 //该弧相关信息的指针
}ArcBox;

typedef struct VexNode{
    VertexType data;
    ArcBox *firstin, *firstout;     //分别指向该顶点第一条入弧和出弧
}VexNode;	

typedef struct{
    VexNode xlist[MAX_VERTEX_NUM];   //表头向量
    int vexnum, arcnum;              //有向图的当前顶点数和弧数
}OLGraph;

只要输入n个顶点的信息和e条弧的信息，便可以建立该有向图的十字链表，其算法7.3如下所示：

Status CreateDG(OLGraph &G)
{
    //采用十字链表存储表示，构造有向图G(G.kind=DG)

    scanf(&G.vexnum,&G.arcnum, &IncInfo);         //IncInfo为0则各弧不含其它信息
    
    //构造表头向量
    for(i = 0; i < G.vexnum; i++)
    {
        scanf(&G.xlist[i].data);                  //输入顶点值           
        G.xlist[i].firstin = NULL;
        G.xlist[i].firstout = NULL;               //初始化指针
    }

    //输入各弧并构造十字链表
    for(k = 0; k < G.arcnum; ++k)
    {
        scanf(&v1, &v2);                          //输入一条弧的始点和终点
        i = LocateVex(G, v1);                     //确定v1和v2在G中的位置
        j = LocateVex(G, v2);

        p = (ArcBox *)malloc(sizeof(ArcBox));     //这里假定有足够空间，不会分配失败
        *p = {i, j, G.xlist[j].firstin, G.xlist[i].firstout, NULL);   //对弧节点赋值
        //   {tailvex, headvex, hlink, tlink, info}

        G.xlist[j].firstin = G.xlist[i].firstout = p;   //完成在入弧和出弧链头的插入

        if(IncInfo)   
            Input(*p->info);                      //若弧含有相关信息，则输入 
       
    }
}

在十字链表中，既容易找到以vi为尾的弧，也容易找到以vi为头的弧，因而容易求得顶点的出度和入度（或需要，可在建立十字链表的同时求出）。同时由上面算法7.3可知，建立十字链表的时间复杂度和建立邻接表是相同的。在某些有向图的应用中，十字链表是很有用的工具。

2.4 邻接多重表

邻接多重表(Adjacency Multilist)是无向图的另一种链式存储结构。虽然邻接表是无向图的一种很有效的存储结构，在邻接表中容易求得顶点和边的各种信息。但是，在邻接表中每一条边(vi,vj)有两个结点，分别在第i个和第j个链表中，这给某些图的操作带来不便。例如，在某些图的应用问题中需要对边进行某种操作，如对已被搜索过的边作记号或删除一条边等，此时需要找到表示同一条边的两个节点。因此，在进行这一类操作的无向图的问题中采用邻接多重表作存储结构更为适宜。

邻接多重表的结构和十字链表类似。在邻接多重表中，每一条边用一个节点表示，它由如下（a)所示的6个域组成：

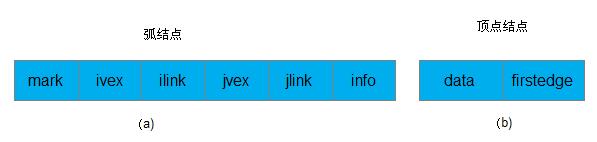
其中，mark为标志域，可以用于标记该条边是否被搜索过； ivex和jvex为该边依附的两个顶点在图中的位置； ilink指向下一条依附于顶点ivex的边； jlink指向下一条依附于顶点jvex的边； info为指向和边相关的各种信息的指针域。

每一个顶点也用一个节点表示，它由上图(b)所示的的两个域组成。其中，data域存储和该顶点相关的信息，firstedge域指示第一条依附于该顶点的边。例如，下图7.12所示为为无向图G2的邻接多重表：

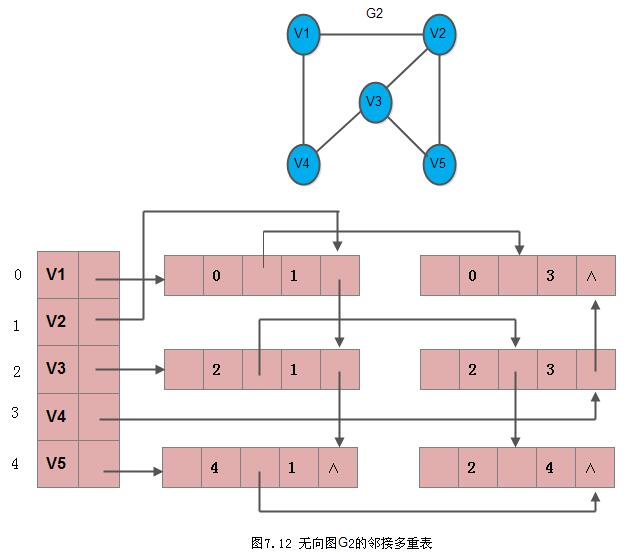
在邻接多重表中，所有依附于同一顶点的边串联在同一链表中，由于每条边依附于两个顶点，则每个边节点同时链接在两个链表中。可见，对无向图而言，其邻接多重表和邻接表的差别，仅仅在于同一条边在邻接表中用两个结点表示，而在邻接多重表中只有一个节点。因此，除了在边结点中增加一个标志域外，邻接多重表所需的存储量和邻接表相同。在邻接多重表上，各种基本操作的实现亦和邻接表相似。邻接多重表的类型说明如下：

//----- 无向图的邻接多重表存储表示--------

#define MAX_VERTEX_NUM 20

typedef enum{unvisited, visited} VisitIf;

typedef struct EBox{
   VisitIf mark;            //访问标记
   int ivex, jvex;          //该边依附的两个顶点的位置
   struct *ilink, *jlink;   //分别指向依附这两个顶点的下一条边
   InfoType *info;          //该边信息指针
}EBox;

typedef struct VexBox{
   VertexType data;
   EBox *firstedge;         //指向第一条依附该顶点的边
}VexBox;

typedef struct{
   VerBox adjmulist[MAX_VERTEX_NUM];   
   int vexnum, edgenum;     //无向图的当前顶点数和边数
}AMLGraph;