树和森林
本节我们将讨论树的表示及其遍历操作,并建立森林与二叉树的对应关系。
1. 树的存储结构
在大量的应用中,人们曾使用多种形式的存储结构来表示树。这里,我们介绍3种常用的链表结构。
1.1 双亲表示法
假设以一组连续空间存储树的结点,同时在每个结点中附设一个指示器指示其双亲节点在链表中的位置,其形式说明如下:
//-------树的双亲表存储表示--------
#define MAX_TREE_SIZE 100
typedef struct PTNode{ //节点结构
TElemType data;
int parent; //双亲位置域
}PTNode;
typedef struct{ //树结构
PTNode nodes[MAX_TREE_SIZE];
int r,n; //根的位置和节点数
}PTree;例如,图6.13展示一棵树及其双亲表示的存储结构。
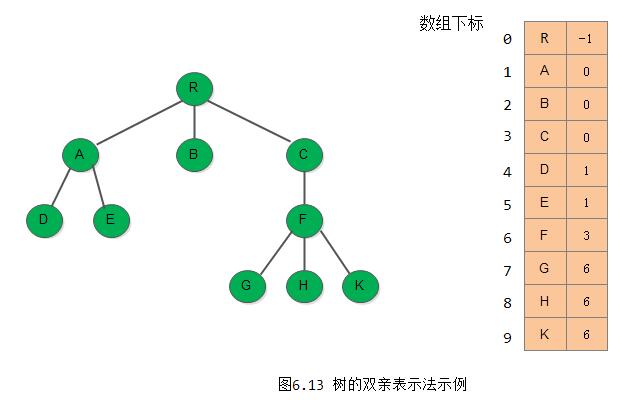
这种存储结构利用了每个节点(除根以外)只有唯一的双亲性质。PARENT(T,x)操作可以在常量时间内实现。反复调用PARENT操作,直到遇到无双亲的节点时,便找到了树的根,这就是ROOT(x)操作的过程。但是在这种表示方法中,求节点的孩子时需要遍历整个结构。
1.2 孩子表示法
由于树中每个节点可能有多棵子树,则可用多重链表,即每个节点有多个指针域,其中每个指针指向一棵子树的根节点,此时链表中的结点可以有如下两种结点格式:

若采用第一种节点格式,则多重链表中的节点是同构的,其中d为树的度。由于树中很多结点的度小于d,所以链表中有很多空链域,空间较浪费,不难推出,在一棵有n个节点度为k的树中必有n(k-1)+1个空链域。若采用第二种结点格式,则多重链表中的节点是不同构的,其中d为节点的度,degree域的值同d。此时,虽能节约存储空间,但操作不方便。
另一种办法是把每个结点的孩子节点排列起来,看成一个线性表,且以单链表做存储结构,则n个节点有n个孩子链表(叶子节点的孩子链表为空表)。而n个头指针又组成一个线性表,为了便于查找,可采用顺序存储结构。这种存储结构可形式地说明如下:
//--------树的孩子链表存储表示----------------
typedef struct CTNode{
int child;
struct CTNode *next;
}*ChildPtr;
typedef struct{
TElemType data;
ChildPtr firstchild; //孩子链表头指针
}CTBox;
typedef struct{
CTBox nodes[MAX_TREE_SIZE];
int n, r; //节点数和根的位置
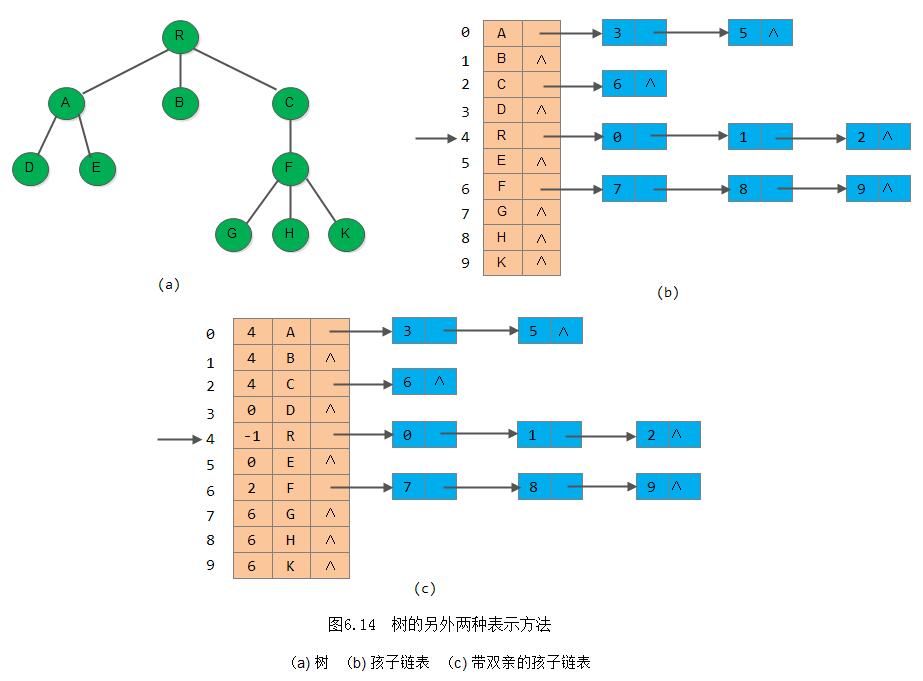
}CTree;下图6.14(b)是图6.14(a)中的树的孩子表示法。与双亲表示法相反,孩子表示法便于那些涉及孩子的操作的实现,却不适用于PARENT(T, x)操作。我们可以把双亲表示法和孩子表示法结合起来,即将双亲表示和孩子链表结合在一起。图6.14(c)就是这种存储结构的一例,它和图6.14(b)表示的是同一棵树。
1.3 孩子兄弟表示法
又称二叉树表示法,或二叉链表示法。即以二叉链表作树的存储结构。链表中结点的两个链域分别指向该结点的第一个孩子节点和下一个兄弟节点,分别命名为firstchild域和nextsibling域。
//------ 树的二叉链表(孩子-兄弟)存储表示--------
typedef struct CSNode{
ElemType data;
struct CSNode *firstchild, *nextsibling;
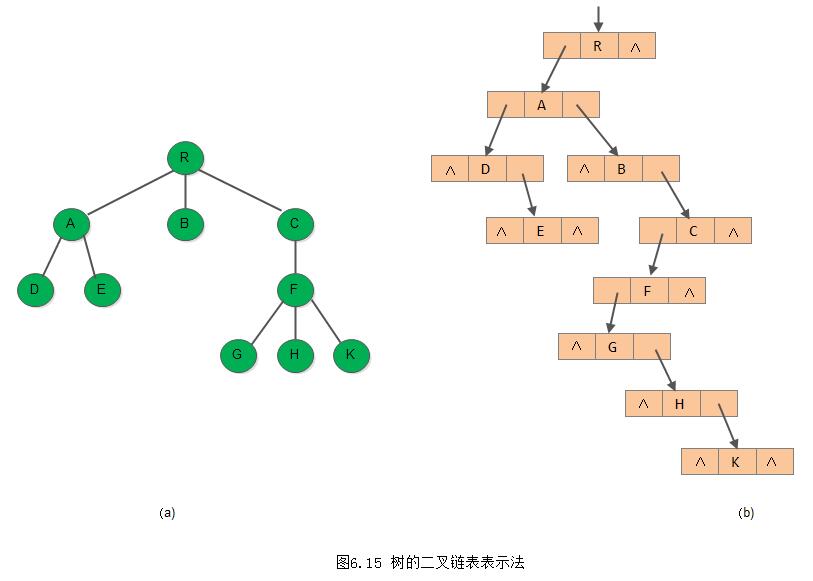
}CSNode, *CSTree;下图6.16(b)就是图6.16(a)中的树的孩子兄弟链表。利用这种存储结构便于实现各种各种树的操作。首先易于实现找结点孩子等的操作。例如:若要访问节点x的第i个孩子,则只要先从firstchild域找到第一个孩子节点,然后沿着孩子结点的nextsibling域连续走i-1步,便可找到x的第i个孩子。当然,如果为每个节点增设一个PARENT域,则同样能方便实现PARENT(T,x)操作。
2. 森林与二叉树的转换
由于二叉树和树都可用二叉链表作为存储结构,则以二叉链表作为媒介可导出树与二叉树之间的一个对应关系。也就是说,给定一棵树,可以找到唯一的一棵二叉树与之对应,从物理结构来看,它们的二叉链表是相同的,只是解释不通而已。下图直观的展示了树与二叉树之间的对应关系。
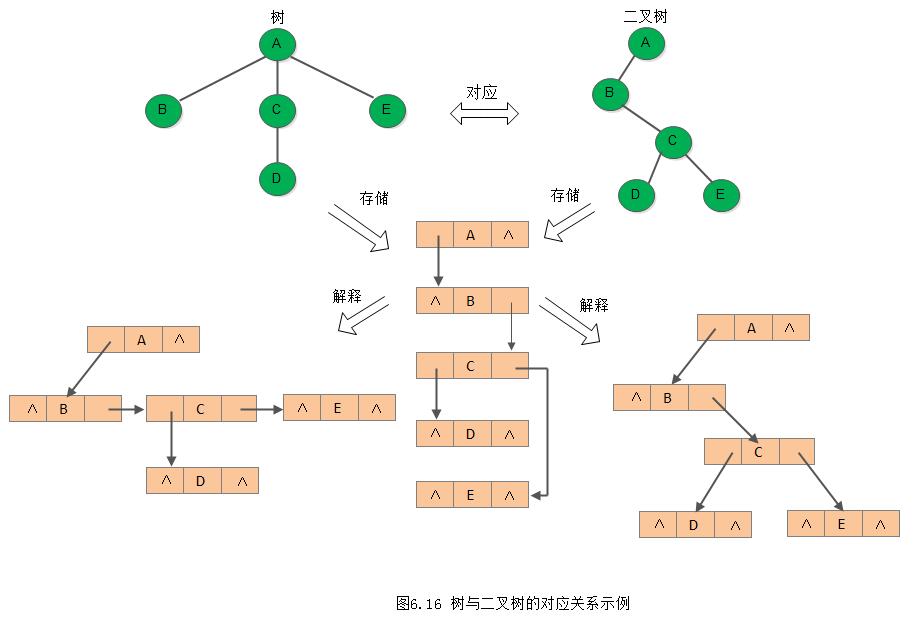
从树的二叉链表表示的定义可知,任何一棵和树对应的二叉树,其右子树必空。若把森林中第二棵树的根结点看成是第一棵树的根结点的兄弟,则同样可导出森林和二叉树的对应关系。
例如,图6.17展示了森林与二叉树之间的对应关系。
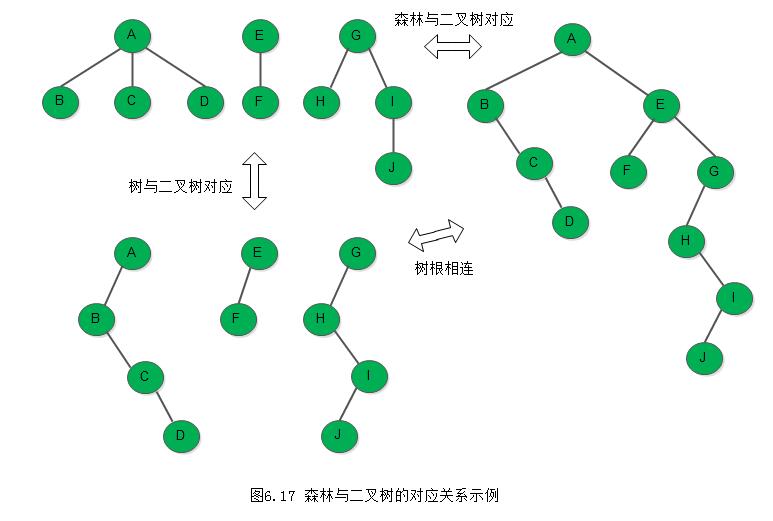
这个一一对应的关系导致森林或树与二叉树可以相互转换,其形式定义如下:
1. 森林转换成二叉树
如果F={T1,T2,…,Tm}是森林,则可按如下规则转换成一棵二叉树B=(root,LB,RB)
1) 若F为空,即m=0,则B为空树;
2) 若F非空,即m!=0,则B的根root即为森林中第一棵树的根ROOT(T1);B的左子树LB是从T1中根节点的子树森林F1={T11,T12,…,T1m1}转换而成的二叉树;其右子树RB是从森林F’={T2,T3,…,Tm}转换而成的二叉树。
下面我们给出一个伪代码实现:
#define MAX_DEGREE 100
typedef struct CSNode{
ElemType data;
struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;
typedef struct TNode{
ElemType data;
struct TNode *children[MAX_DEGREE];
}TNode, *Tree;
void transform(Tree trees[], int num, CSTree *out)
{
if(num == 0){
*out = NULL;
return;
}
i = 0;
while(i < MAX_DEGREE && trees[0].children[i]){
i++;
}
transform(trees[0].children, i, &(*out)->firstchild);
transform(trees[1], num-1, &(*out)->nextsibling);
} 2. 二叉树转换成森林
如果B=(root, LB, RB)是一棵二叉树,则可按如下规则转换成森林F={T1, T2, …, Tm}
1) 若B为空,则F为空;
2) 若B非空,则F中第一棵树T1的根ROOT(T1)即为二叉树B的根root; T1中根节点的子树森林F1是由B的左子树LB转换而成的森林; F中除T1之外的其余树组成的森林F’={T2, T3, …, Tm}是由B的右子树RB转换而成的森林。
从上述递归定义容易写出相互转换的递归算法。同时,森林和树的操作亦可转换成二叉树的操作来实现。
下面我们给出一个伪代码实现:
#define MAX_DEGREE 100
typedef struct CSNode{
ElemType data;
struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;
typedef struct TNode{
ElemType data;
struct TNode *children[MAX_DEGREE];
}TNode, *Tree;
void transform(CSTree root, Tree *trees[])
{
if(root == NULL){
*trees[0] = NULL;
return;
}
struct TNode *node = alloc_tnode();
node->data = root->data;
*trees[0] = node;
transform(root->firstchild, node->children);
transform(root->nextsibling, trees+1);
}3. 树和森林的遍历
由树结构的定义可引出两种次序遍历树的方法:一种是先根(次序)遍历树,即:先访问树的根节点,然后依次先根遍历根的每棵子树;另一种是后根(次序)遍历,即:先依次后根遍历每颗子树,然后访问根节点。
例如,有如下树:
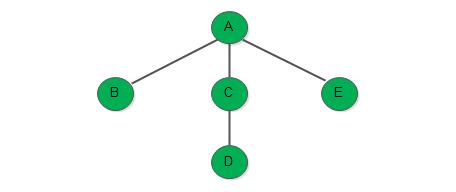
对树进行先根遍历,可得树的先根序列为:
A B C D E
若对此树进行后根遍历,则得树的后根序列为:
B D C E A按照森林和树相互递归的定义,我们可以推出森林的两种遍历方法: ###### 先序遍历森林 若森林非空,则可按下述规则遍历之: 1) 访问森林中第一棵树的根结点; 2) 先序遍历第一棵树中根结点的子树森林; 3) 先序遍历除去第一棵树之后剩余的树构成的森林 ###### 中序遍历森林 若森林非空,则可按下述规则遍历之: 1) 中序遍历森林中第一棵树的根结点的子树森林 2) 访问第一棵树的根结点; 3) 中序遍历除去第一棵树之后剩余的树构成的森林。 例如,有如下森林: 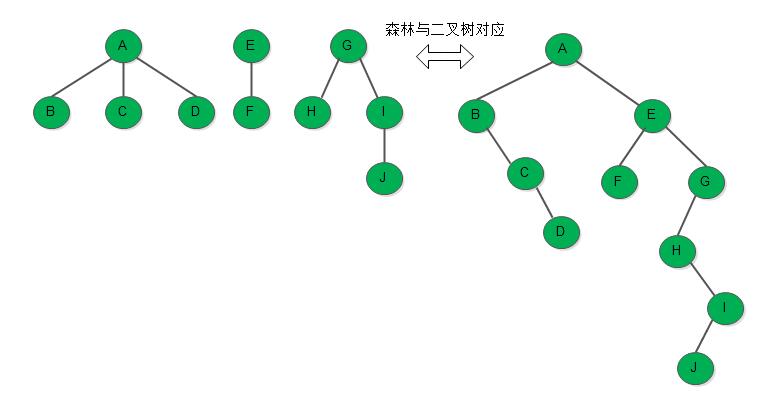 若对森林进行先序遍历和中序遍历,则分别得到森林的先序序列为:A B C D E F G H I J中序序列为:B C D A F E H J I G由上节森林与二叉树之间转换的规则可知,当森林转换成二叉树时,其第一棵树的子树森林转换成左子树,剩余的森林转换成右子树,则上述森林中的先序和中序遍历即为其对应的二叉树的先序和中序遍历。若对上图中和森林对应的二叉树进行先序和中序遍历,可得和上述相同的序列。 由此可见,当以二叉链表作为树的存储结构时,树的先根遍历和后根遍历可借用二叉树的先序遍历和后续遍历的算法实现之。
**[参看]:**

