本章我们介绍一下树与等价问题。

1. 树与等价问题

在离散数学中，对等价关系和等价类的定义是：

如果集合S中的关系是自反的、对称的和传递的，则称它为一个等价关系。

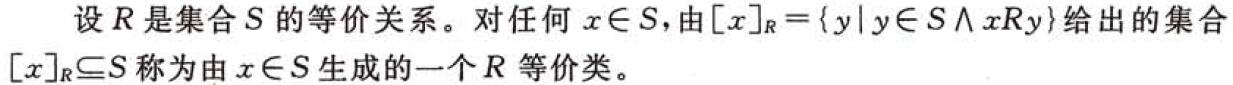
若R是集合S上的一个等价关系，则由这个等价关系可产生这个集合的唯一划分。即可以按R将S划分为若干不相交的子集S1，S2， …，它们的并集即为S，则这些子集Si便称为S的R等价类。

这里我们介绍一下集合上关系的自反性、对称性和传递性：

1） 自反性(reflexive)
定义： 设R为定义在集合A上的二元关系，如果对于每个x∈A，都有<x,x>∈R，即xRx，则称二元关系R是自反的

2） 对称性(symmetric)
定义： 设R为定义在集合A上的二元关系，如果对于每个x,y∈A，每当<x,y>∈R，就有<y,x>∈R，则称集合A上的关系R是对称的。

3）传递性(transitive)
定义： 设R为定义在集合A上的二元关系，如果对于任意的x,y,z∈A，每当<x,y>∈R且<y,z>∈R，就有<x,z>∈R，称关系R在A上是传递的。

如下我们举个例子：
R1={<a,a>, <a,b>, <b,a>, <c,c>}              ===> 关系R1是对称的

R2={<a,a>, <a,b>, <b,a>, <b,b>, <c,c>}       ===> 关系R2是自反的、对称的、传递的


下面我们介绍一下等价关系。
定义：设R为定义在集合A上的一个关系，若R是自反的、对称的和传递的，则称R为集合A上的等价关系。

例如：
1） 平面上三角形集合中，三角形的相似关系

2） 同学集合A={a,b,c,d,e,f,g}，A中的关系R: 住在同一宿舍

3） 同性关系


下面我们介绍一下等价类。
定义： 设R为定义在集合A上的一个关系，对任意的a∈A，集合
       [a]R = {x|x∈A, <a,x>∈R}
      称为元素a关于R的等价类

例如：设A={1，2，3，...，8},如下定义A上的关系R：
     R={<x,y>|x,y∈A且x≡y (mod3)}
     则，我们可以求得如下3个等价类：

    [1]R = [4]R = [7]R = {1,4,7}
    [2]R = [5]R = [8]R = {2,5,8}
    [3]R = [6]R = {3,6}  

等价关系是现实世界中广泛存在的一种关系，许多应用问题可以归结为按给定的等价关系划分某集合为等价类，通常称这类问题为等价问题。

例如在FORTRAN语言中，可以利用EQUIVALENCE语句使数个程序变量共享同一存储单位，这问题实质就是按EQUIVALENCE语句确定的关系对程序中的变量集合进行划分，所得等价类的数目即为需要分配的存储单位，而同一等价类中的程序变量可被分配到同一存储单位中去。此外，划分等价类的算法思想也可用于求网络的最小生成树等图的算法中。

应如何划分等价类呢？ 假设集合S有n个元素，m个形如(x,y)(x,y ∈S)的等价偶对确定了等价关系R，需求S的划分。

确定等价类的算法可如下进行：

1） 令S中每个元素各自形成一个只含单个成员的子集，记作S1,S2,…,Sn。

2） 重复读入m个偶对，对每个读入的偶对(x,y)，判断x和y所属子集。不失一般性，假设x∈Si，y∈Sj，若Si != Sj，则将Si并入Sj并置Si为空（或将Sj并入Si并置Sj为空）。则当m个偶对都处理过后，S1,S2,…,Sn中所有非空子集即为S的R等价类。

从上述可见，划分等价类需要对集合进行的操作又3个： 其一是构造只含单个成员的集合；其二是判定某个单元素所在的子集；其三是归并两个互不相交的集合为一个集合。由此，需要一个包含上述3中操作的抽象数据类型MFSet。

ADT MFSet{
  数据对象： 若S是MFSet型的集合，则它由n(n>0)个子集Si(i=1,2,...,n)构成，每个子集的成员都是
           子界[-maxnumber..maxnumber]内的整数；
  数据关系： S1 ∪ S2 ∪ ... ∪ Sn = S   Si ⊆ S(i=1,2,...,n)
  基本操作：
Initial(&S,n,x1,x2,...,xn);
  操作结果： 初始化操作。构造一个由n个子集（每个子集只含单个成员xi)构成的集合S。

Find(S,x);
  初始条件： S是已存在的集合，x是某个子集的成员
  操作结果： 查找函数。确定S中x所属子集Si。

Merge(&S, i, j);
  初始条件： Si和Sj是S中两个互不相交的非空集合。
  操作结果： 归并操作。将Si和Sj中的一个并入另一个中。
 
}ADT MFSet;

以集合为基础（结构）的抽象数据类型可用多种实现方法，如用位向量表示集合或用有序表表示集合等。如何高效地实现以集合为基础的抽象数据类型，则取决于该集合的大小以及对此集合所进行的操作。根据MFSet类型中定义的查找函数和归并操作的特点，我们可利用树型结构表示集合。约定： 以森林F=(T1,T2,…,Tn)表示MFSet型的集合S，森林中的每一颗树Ti(i=1,2,…,n)表示S中的一个元素————自己Si(Si ⊆ S, i=1,2,…,n)，树中每个节点表示子集中的一个成员x，为操作方便起见，令每个节点中含有一个指向其双亲的指针，并约定根结点的成员兼作子集的名称。例如，图6.18(a)和(b)中的两棵树分别表示子集S1={1,3,6,9}和S2={2,8,10}。显然，这样的树形结构易于实现上述两种集合的操作。由于各子集中的成员均不相同，则实现集合的并操作，只要将一棵子集树的根指向另一棵子集树的根即可。例如：图6.18(c)中S3=S1∪S2。同时，完成找某个成员所在集合的操作，只要从该成员节点出发，顺链而进，直至找到树的根节点为止。

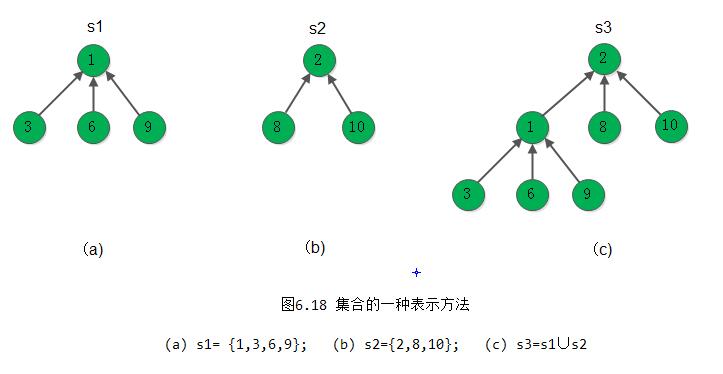
为了实现这样两种操作，应采用双亲表示法作存储结构，如下所示：

算法6.8:

//-----------ADT MFSet 的树的双亲表存储表示-----------
typedef PTree MFSet;

int find_mfset(MFSet S, int i)
{
	//找集合S中i所在子集的根

	if(i < 1 || i > S.n)
		return -1;             //i不属S中任一子集
		
	for(j = i; S.nodes[j].parent > 0; j = S.nodes[j].parent);

	return j;
}

算法6.9:

Status merge_mfset(MFSet &S, int i, int j)
{
	//S.nodes[i]和S.nodes[j]分别为S的互不相交的两个子集Si和Sj的根节点
	//求并集Si∪Sj
	
	if(i <1 || j > S.n || j < 1 || j > S.n)
		return ERROR;
		
	S.nodes[i].parent = j;

	return OK;
}

算法6.8和算法6.9的时间复杂度分别为O(d)和O(1)，其中d是树的深度。从前面的讨论可知，这种表示集合的树的深度和树形成的过程有关。试看一个极端的例子。假设有n个子集S1，S2，…，Sn，每个子集只有一个成员Si={i}(i=1,2,…,n)，可用n棵只有一个根结点的的树表示，如图6.19(a)表示。现作n-1次“并”操作，并假设每次都是含成员多的根节点指向含成员少的根节点，则最后得到的集合树的深度为n，如图6.19(b)所示。如果再加上在每次“并”操作之后都要进行查找成员“1”所在子集的操作，则全部操作的时间便是O(n^2)了。

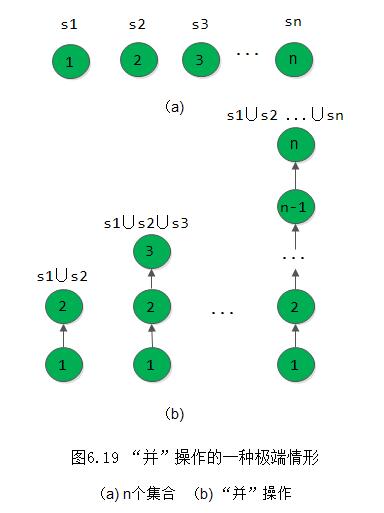
改进的办法是在作“并”操作之前先判别子集中所含成员的数目，然后令含成员少的子集树根结点指向含成员多的子集的根。为此，需相应地修改存储结构： 令根节点的parent域存储子集中所含成员数目的负值。修改后的“并”操作算法如算法6.10所示：

算法6.10:

void mix_mfset(MFSet &S, int i, int j)
{
	//S.nodes[i]和S.nodes[j]分别为S的互不相交的两个子集Si和Sj的根节点。
	//求并集Si∪Sj
	
	if(i < 1 || i > S.n || j < 1 || j > S.n)
		return ERROR;
		
	if(S.nodes[i].parent > S.nodes[j].parent){
		//Si所含成员数比Sj少
		S.nodes[j].parent += S.nodes[i].parent;
		S.nodes[i].parent = j;
	}else{
		S.nodes[i].parent += S.nodes[j].parent;
		S.nodes[j].parent = i;
	}

	return OK;
}

可以证明，按算法6.10进行“并”操作得到的集合树，其深度不超过⌊log2^n⌋+1，其中n为集合S中所有子集所含成员数的总和。

由此，利用算法find_mfset和mix_mfset解等价问题的时间复杂度为O(nlog2^n)(当集合中有n个元素时，至多进行n-1次mix操作）。

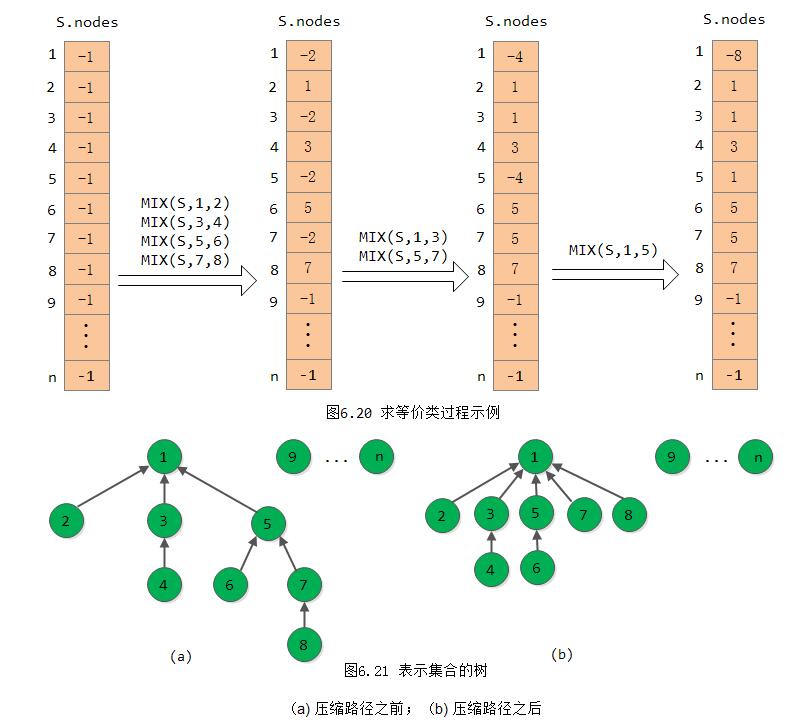
以MFSet类型的变量S表示集合S，S中的成员个数为S.n。开始时，由于每个成员自成一个等价类，则S.nodes[i].parent的值均为-1。之后，每处理一个等价偶对(i,j)，首先必须确定i和j各自所属集合，若这两个集合相同，则说明此等价关系是多余的，无需作处理；否则就合并这两个集合。图6.20展示了处理R中前7个等价关系时S的变化状况（图中省去了节点的数据域），图6.21(a)所示为和最后一个S状态相应的树的形态。显然，随着子集逐对合并，树的深度也越来越大，为了进一步减少确定元素所在集合的时间，我们还可进一步将算法6.8改进为算法6.11。当所查元素i不在树的第二层时，在算法中增加一个“压缩路径”的功能，即将所有从根到元素i路径上的元素都变成树根的孩子。

算法6.11

int fix_mfset(MFSet &S, int i)
{
	//确定i所在子集，并将从i至根路径上所有结点都变成根的孩子节点
	
	if(i < 1 || i > S.n)
		return -1;          //i不是S中任一子集的成员
		
	for(j = i; S.nodes[j].parent > 0; j = S.nodes[j].parent);

	for(k = i; k != j; k = t){
		
		t = S.nodes[k].parent;
		S.nodes[k].parent = j;
	}
	
	return j;
}

假设例6-1中R的第8个等价偶对为(8,9)，则在执行fix(S,8)的操作之后图6.21(a)的树就变成6.21(b)的树。

已经证明，利用算法fix_mfset和mix_mfset划分大小为n的集合为等价类的时间复杂度为O(nα(n))。其中α(n)是一个增长极其缓慢的函数，若定义单变量的阿克曼函数为A(x) = A(x,x)，则函数α(n)定义为A(x)的拟逆，即α(n)的值是使A(x)≥n成立的最小x。所以，对于通常所见到的正整数n而言，α(n)≤4。

[参看]:

1. 等价关系与等价类