本章我们主要介绍以下静态树表的查找。

1. 静态树表的查找

一般情况下我们对有序表的查找性能的讨论是在等概率的前提下进行的，即当有序表中各记录的查找概率相等时，对有序表进行折半查找，其性能最优。如果有序表中各记录的查找概率不等，情况又如何呢？

下面我们先看一个具体的例子。假设有序表中含5个记录，并且已知各记录的查找概率不等，分别为P1=0.1, P2=0.2, P3=0.1, P4=0.4和P5=0.2。如对此有序表进行折半查找，查找成功时的平均查找长度为：

5
∑PiCi = 0.1 x 2 +  0.2 x 3 + 0.1 x 1 + 0.4 x 2 + 0.2 x 3 = 2.3
i=1

但是，如果在查找时令给定值先和第4个记录的关键字进行比较，比较不相等时，再继续再左子序列或右子序列进行折半查找，则查找成功时的平均查找长度为：

5
∑PiCi = 0.1 x 3 +  0.2 x 2 + 0.1 x 3 + 0.4 x 1 + 0.2 x 2 = 1.8
i=1

这就说明，当有序表中各记录的查找概率不等时，对有序表进行简单的折半查找，其性能未必是最优的。那么，此时应如何进行查找呢？ 换句话说，描述查找过程的判定树为何类二叉树时，其查找性能最优？

如果只考虑查找成功的情况，则使查找性能达最佳的判定树是其带权内路径长度之和PH值

     n
PH = ∑WiHi 
     i=1

取最小值的二叉树。其中：n为二叉树上节点的个数（即有序表的长度）； Hi为第i个节点在二叉树上的层次数；节点的权Wi=CPi（i=1,2,…,n)，其中Pi为节点的查找概率，C为某个常量。称PH值取最小的二叉树为静态最优查找树(Static Optimal Search Tree)。由于构造静态最优查找树花费的时间代价比较高，因此这里不做介绍。下面我们讲述一种构造近似最优查找树的有效算法。

由此，可得构造次优查找树的递归算法如下：

//由有序表R[low...high]及其累计权值sw(其中sw[0]==0)递归构造次优查找树T
void SecondOptimal(BiTree *T, ElemType R[], float sw[],int low, int high)
{
	i = low;
	min = abs(sw[high]-sw[low]);
	dw = sw[high] + sw[low-1];

	//选择最小的∆Pi值
	for(j = i+1;j<=high;++j)    
	{
		if(abs(dw - sw[j] - sw[j-1]) < min)
		{
			i = j;
			min = abs(dw-sw[j]-sw[j-1]);
		}
	}

	*T = (BiTree)malloc(sizeof(BiNode));
	(*T)->data = R[i];
	if(i == low)
		(*T)->lchild = NULL;
	else
		SecondOptimal(&(*T)->lchild, R, sw, low, i-1);		//构造左子树

	if(i == high)
		(*T)->rchild = NULL;
	else
		SecondOptimal(&(*T)->rchild, R, sw, i+1, high);		//构造右子树
}

2. 次优查找树示例

1) 示例1

已知含9个关键字的有序表及其对应的权值为：

关键字   A   B   C   D   E   F   G   H   I
 权值    1   1   2   5   3   4   4   3   5

则按算法SecondOptimal()构造次优查找树的过程中累计权值SW和∆P的值如下图(a)所示，构造所得次优二叉查找树如下图(b)所示：

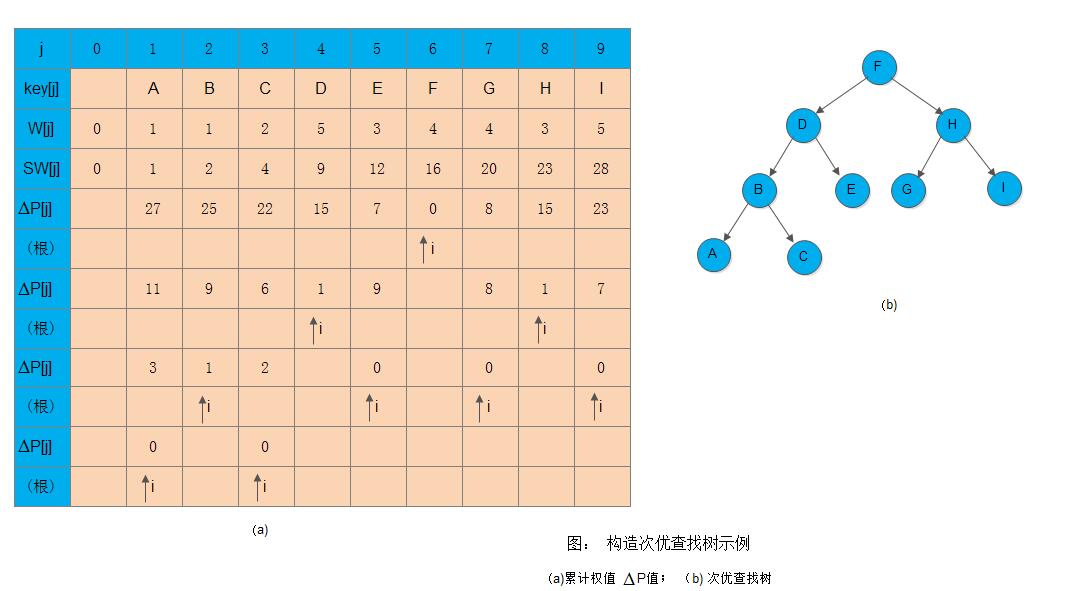
由于在构造次优查找树的过程中，没有考察单个关键字的相应权值，则有可能出现被选为根的关键字的权值比与它相邻的关键字的权值小。此时应作适当的调整： 选取邻近的权值较大的关键字作为次优查找树的根节点。

2) 示例2

已知含5个关键字的有序表及其相应的权值为：

关键字   A   B   C   D   E   
 权值    1  30   2  29   3   

则按算法SecondOptimal()构造次优查找树如下图(a)所示，调整处理后次优查找树如下图(b)所示。容易算得，前者的PH值为132，后者的PH值为105.

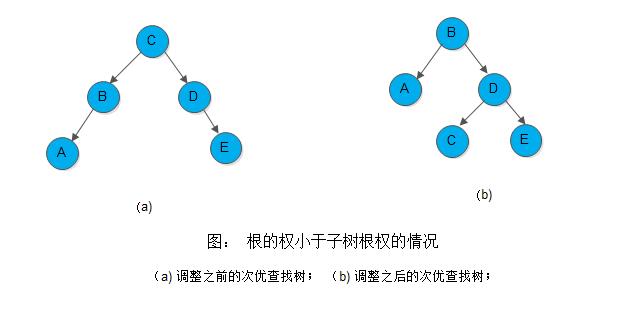
3. 次优查找树查找性能

大量的实验研究证明，次优查找树和最优查找树的查找性能之差仅为1%~2%，很少超过3%，而且构造次优查找树的算法的时间复杂度为nlogn，因此算法SecondOptimal()是有效的。

从次优查找树的结构特点可见，其查找过程类似于折半查找。若次优查找树为空，则查找不成功，否则，首先将给定值key和其根节点的关键字相比较，若相等则查找成功，该根节点的记录即为所求； 否则将根据给定值key小于或大于根节点的关键字而分别在左子树或右子树中继续查找直至查找成功或不成功为止。由于查找过程恰是走了一条从根到待查记录所在节点（或叶子节点）的一条路径，进行过比较的关键字个数不超过树的深度，因此，次优查找树的平均查找长度和logn成正比。可见，在记录的查找概率不等时，可用次优查找树表示静态树，故又称静态树表，按有序表构造次优查找树的算法如下：

typedef BiTree SOSTree;		//次优查找树采用二叉链表的存储结构

//由有序表ST构造一棵次优查找树。ST的数据元素含有权域weight
Status CreateSOSTree(SOSTree *T,SSTable ST)
{
	if(ST.length == 0)
		*T = NULL;
	else{
		//按照有序表ST中各数据元素的weight域求累计权值表sw
		FindSW(sw,ST);

		SecondOptimal(T,ST.elem,sw, 1, ST.length);
	}

	return OK;
}