回溯法与树的遍历
本章我们讲述一下回溯法与树的遍历。
1. 回溯法与树的遍历
在程序设计中,有相当一类求一组解、或求全部解或求最优解的问题,例如读者所熟悉的八皇后问题等,不是根据某种确定的计算法则,而是利用试探和回溯(backtracking)的搜索技术求解。回溯法也是设计递归过程的一种重要方法,它的求解过程实质上是一个先序遍历一棵“状态树”的过程,只是这棵树不是遍历前预先建立的,而是隐含在遍历过程中,但如果认识到这点,很多问题的递归过程设计也就迎刃而解了。为了说明问题,先看一个简单的例子。
例6-3: 求含n个元素的集合的幂集
集合A的幂集是由集合A的所有子集所组成的集合。如: A={1,2,3},则A的幂集:

当然,可以用5.7节介绍的分治法来设计这个求幂集的递归过程。在此,从另一角度分析问题。幂集的每个元素是一个集合,它或是空集,或含集合A中一个元素,或含集合A中两个元素,或等于集合A。反之,从集合A的每个元素来看,它只有两种状态: 它或属幂集的元素集,或不属幂集元素集。则求幂集ρ(A)的元素的过程可看成是依次对集合A中元素进行“取”或“舍(弃)”的过程,并且可以用一棵如下图6.28所示的二叉树,
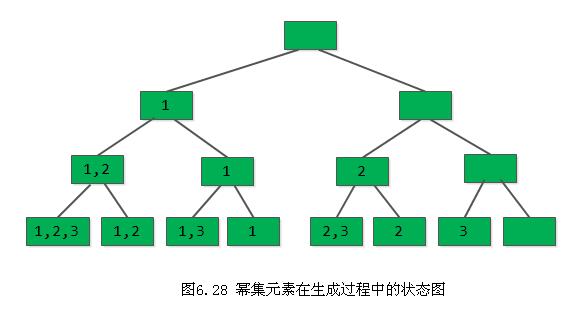
来表示过程中过程中幂集元素的状态变化状况,树中的根结点表示幂集元素的初始状态(为空集);叶子节点表示它的终结状态(如图6.28中8个叶子节点表示式(6-6)中幂集ρ(A)的8个元素);而第i(i=2,3,…, n-1)层的分支节点,则表示已对集合中前i-1个元素进行了取/舍处理的当前状态(左分支表示“取”,右分支表示“舍”)。因此,求幂集元素的过程即为先序遍历这棵状态树的过程,如算法6.14所描述。
算法6.14
void PowerSet(int i, int n)
{
//求含n个元素的集合A的幂集ρ(A)。进入函数时已对A中前i-1个元素作了取舍处理
//现从第i个元素起进行取舍处理。若i>n,则求得幂集的一个元素,并输出之
//初始条用PowerSet(1,n);
if(i > n){
输出幂集的一个元素
}
else{
取第i个元素; PowerSet(i+1, n);
舍第i个元素; PowerSet(i+1, n);
}
}对算法6.14求精需确定数据结构。假设以线性表表示集合,则求精后的算法如算法6.15所示。
算法6.15
void GetPowerSet(int i, List A, List &B)
{
//线性表A表示集合A,线性表B表示幂集ρ(A)的一个元素
//局部量k为进入函数时表B的当前长度。第一次调用本函数时,B为空表,i=1
if(i > ListLength(A))
Output(B); //输出当前B值,即ρ(A)的一个元素
else{
GetElem(A, i, x);
k = ListLength(B);
ListInsert(B, k+1, x); GetPowerSet(i+1, A, B);
ListDelete(B, k+1, x); GetPowerSet(i+1, A, B);
}
}图6.28中的状态变化树是一棵满二叉树,树中每个叶子节点的状态都是求解过程中可能出现的状态(即问题的解)。然而,很多问题用回溯和试探求解时,描述求解过程的状态树不是一棵满的多叉树。当试探过程中出现的状态和问题所求解产生矛盾时,不再继续试探下去,这时出现的叶子节点不是问题的解的终结状态。这类问题的求解过程可看成是在约束条件下进行先序(根)遍历,并在遍历过程中剪去那些不满足条件的分支。
例6-4 求4皇后问题的所有合法布局(作为例子,我们将8皇后问题简化为4皇后问题)
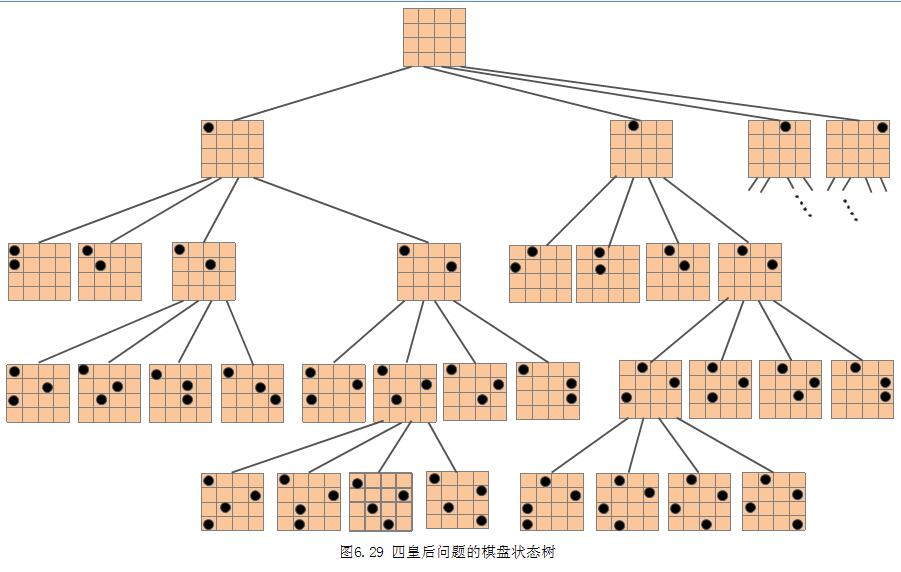
图6.29展示求解过程中棋盘状态的变化情况。这是一棵四叉树,树上每个结点表示一个局部布局或一个完整的布局。根结点表示棋盘的初始状态:棋盘上无任何棋子。每个(皇后)棋子都有4个 选择的位置,但在任何时刻,棋盘的合法布局都必须满足3个约束条件,即任何两个棋子都不占据棋盘上的同一行、或者同一列、或者同一对角线。
求所有合法布局的过程即为在上述约束条件下先根遍历图6.29的状态树的过程。遍历中访问节点的操作为,判别棋盘上是否已得到一个完整的布局(及棋盘上是否已摆上4个棋子)。若是,则输出该布局;否则依次先根遍历满足约束条件的各棵子树,即首先判断该子树根的布局是否合法,若合法,则先根遍历该子树,否则剪去该子树分支。算法6.16为求所有合法布局的伪代码。
算法6.16:
void Trial(int i, int n)
{
//进入本函数时,在nxn棋盘前i-1行已放置了互不攻击的i-1个棋子
//现从第i行起继续为后续棋子选择合适的位置
//当i>n时,求得一个合法布局,则输出之
if(i >n){
输出棋盘的当前布局; //n为4时,即为4皇后问题
}
else{
在第i行第j列放置一个棋子;
if(当前布局合法)
Trial(i+1, n);
移走第i行第j列的棋子;
}
}算法6.16可进一步求精,在此从略。算法6.16可作为回溯法求解的一般模式,类似问题有骑士游历、迷宫问题、选最优解问题等等。
下面我们给出一个完整的8皇后问题的算法:
#include <stdio.h>
#define N 8
int chess[N][N] = {0};
int count = 0;
/*
* Description: 当前棋盘处于安全状态,假设现在要在(r,c)位置放入一颗棋子,
* 放入后是否仍处于安全状态
*
* Return: 0 ---- Dangerous 1--- safe
*/
int notDanger(int row, int col)
{
int i,j;
//1) 判断row行上是否已经有棋子
for(i = 0; i < N; ++i){
if(chess[row][i])
return 0;
}
//2) 判断col列上是否已经有棋子
for(i = 0; i < row; ++i){
if(chess[i][col])
return 0;
}
//3) 判断左上对角是否有棋子
for(i = row -1, j = col-1; i>=0 && j>=0; --i,--j){
if(chess[i][j])
return 0;
}
//4) 判断右上对角是否有棋子
for(i = row-1, j = col+1; i>=0 && j<N; --i,++j){
if(chess[i][j])
return 0x0;
}
return 1;
}
/*
* Description: 打印结果
*/
void Print()
{
int row,col;
printf("第 %d 种\n", count+1);
for(row = 0; row < N; row++){
for(col = 0; col < N; col++){
if(chess[row][col]== 1) //皇后用'0'表示
printf("0 ");
else
printf("# ");
}
printf("\n");
}
printf("\n");
}
/*
* Description: 进入本函数时,在nxn棋盘前i-1行已放置了互不攻击的i-1个棋子
* 现从第i行起继续为后续棋子选择合适的位置
*/
void NQueue(int i)
{
int col;
//如果遍历完N行都找到放置皇后的位置则打印
if(i > N-1){
//打印n皇后的解
Print();
count++;
return;
}
for(col = 0; col < N; col++){
if(notDanger(i, col)){ //判断是否危险
chess[i][col] = 1;
NQueue(i+1);
chess[i][col] = 0; //清零, 以免回溯时出现脏数据
}
}
}
int main(int argc, char *argv[])
{
NQueue(0);
printf("总共有%d种解决方法!\n\n", count);
return 0x0;
}
[参看]:

