动态规划算法题集
本文介绍一些使用动态规划算法来求解题集,以进一步加深对动态规划算法的理解。
1. 瓷砖铺贴问题
题目描述
有一块大小是2*n的墙面,现在需要用两种规格的瓷砖铺满,瓷砖规格分别为2*1和2*2,请计算一共有多少种铺设方法。
输入
输入的第一行包含一个正整数T(T<=20),表示一共有T组数据,接着是T行数据,每一行包含一个正整数N(N<=30),表示墙面的大小是2行N列。
输出
输出一共有多少种铺设的方法,每组数据的输出占一行
样例输入
3 2 8 12
样例输出
3 171 2731
1.1 动态规划求解
本题用动态规划来解决比较简单。我们先找出动态规划的递推式:在进行瓷砖铺贴时有两种砖可选择,设2*1的砖为A,2*2的砖为B。
1)当我们在最开始铺上A砖时,有两种选择
-
竖着铺A砖,此时后面砖的铺法就是dp[i-1]
-
横着铺A砖,此时后面砖的铺法就是dp[i-2]
2) 当我们在最开始铺B砖时,只有一种选择
- B砖占据前面四个格子,则后面砖的铺法就是dp[i-2]
综上得出递推公式:
dp[1] = 1 dp[2] = 3 dp[i] = dp[i - 1] + 2 * dp[i - 2]
由上述递推式写出代码如下:
#include<iostream>
using namespace std;
void solve(long long *dp, int n)
{
dp[1] = 1;
dp[2] = 3;
// start calculating from 3
for (int i = 3; i <= n; i++)
dp[i] = dp[i - 1] + 2 * dp[i - 2];
}
int main(int argc, char *argv[]){
long long dp[33];
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
solve(dp, n);
cout<<dp[n]<<endl;
for(int i = 1; i <= n; i++)
cout<<dp[i]<<" ";
cout<<endl;
}
return 0x0;
}2. 铺瓷砖问题(状态压缩动态规划)
本题转载自铺瓷砖问题(状态压缩动态规划)
2.1 问题简单描述
在一个N行M列的格子里,现有1*2大小的瓷砖,可以横着或者竖着铺。问一共有多少种方案,可以将整个N*M的空间都填满。
示例:
- N=2,M=4时,一共5种方案

- N=2,M=3时,一共3种方案
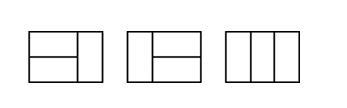
2.2 问题分析
1) 因为每块砖的面积是2,所以总面积M*N必须是偶数才能铺满。如果是基数,则方案数显然为0.
2)分析一下覆盖的状态,用二进制来代表具体覆盖的方案:
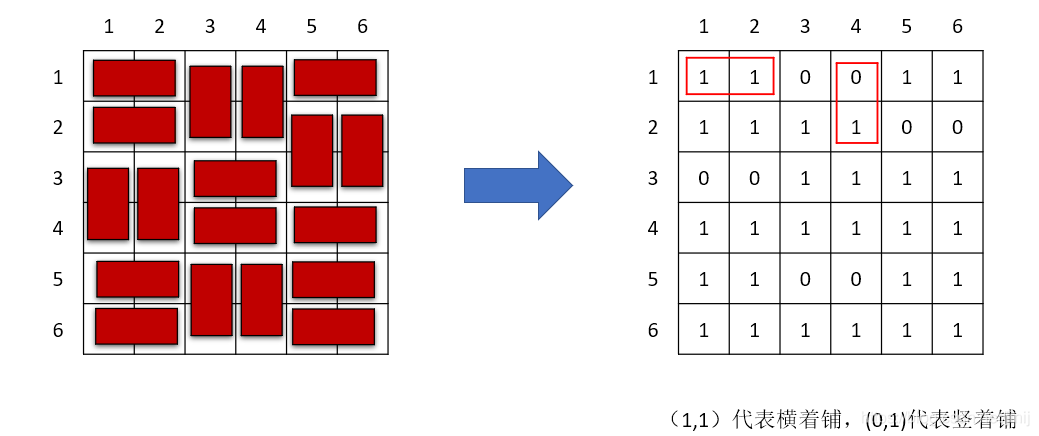
用二进制来代表每一行的覆盖状态:(0,1)代表竖着铺,(1,1)代表横着铺。
铺满的时候最后一排必然全部都是1。
状态转移
此问题的状态转移比较复杂: 上一行的某个状态对应当前行的多个状态;当前行的某个状态也可以来自上一行的多个状态。
状态转移示意图如下:
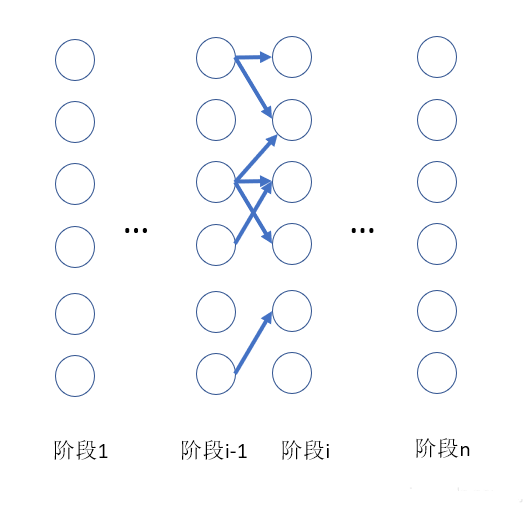
通过观察我们可以看到上一行到下一行状态转移的关系如下:
(注: 此处
上一格代表上一行同一列位置的格子,后一格代表同一行右侧的格子)
对于当前行的某一格来说:
1) 如果上一格是0,当前格必须是1
2) 如果上一格是1
2.1) 当前格可以是0,也可以是1,说明既可以竖着铺,也可以横着铺
2.2) 如果当前格是横铺的第一个1,则后一格必须也是1,并且后一格的上一格不能为0
据此我们可以设计判断当前行能否从上一行状态转移过来的逻辑。
参看如下例子:
- 合法转移
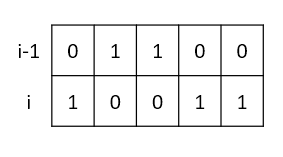
dp[i][10011] += dp[i-1][01100]
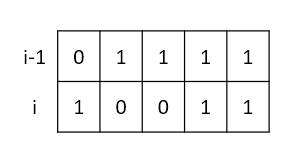
dp[i][10011] += dp[i-1][01111]
- 无法转移
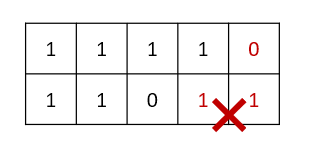
初始状态
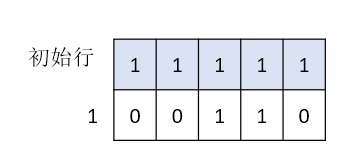
第一行是没有上一行的,为了避免单独写第一行的逻辑。我们可以假设在第一行之上还存在初始行,我们把初始行的状态设为全1的时候方案为1,其他状态方案为0。 这样同样的逻辑我们可以转移到合法的第一行状态。
(注意:初始行只是提供初始状态,不需要考虑初始行本身全1是否合法)
2.3 代码实现
具体代码如下:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
/*
* Description: validate whether current line is legal or not
* upper: represent a situation of last line
* lower: represent a situation of current line
* width: represent the column number
*/
bool validateLines(int upper, int lower, int width)
{
//iterator every column
for(int i=0; i<width;){
if(((upper>>i)&1) == 0){
//retrieve every grid of last line
//if the grid of last line is 0, then the corresponding grid of current line must be 1
if(((lower>>i)&1) == 0){
return false;
}
i++;
}else if(((lower>>i)&1) != 0){
// upper and current line grid is 1
if(i == width-1 || ((lower>>(i+1))&1) == 0 || ((upper>>(i+1)&1)==0) ){
return false;
}else{
i+=2;
}
}else{
// upper grid is 1, current grid is 0.
i++;
}
}
return true;
}
long long int getCoverWays(int rows, int cols)
{
// the size of area must be even.
if((rows*cols)%2 != 0){
return 0;
}
// make sure columns is smaller;
if(cols>rows){
swap(rows,cols);
}
const int STATE_LIMIT = 1<<cols;
//Note: represent two lines
vector<vector<long long int> > dp(2, vector<long long int>(STATE_LIMIT,0));
int cur = 0;
/*
* set the initial state before first line
* dp[cur][STATE_LIMIT-1]=1 means the last situation of last line is valid
*/
dp[cur][STATE_LIMIT-1] = 1;
for(int i=0; i<rows; i++){
cur ^= 1; // switch to current line
std::fill(dp[cur].begin(), dp[cur].end(), 0); // clear the states
/*
* every line has STATE_LIMIT situations(eg: col is 3, there's 8 situations
*
* situation 0: 0b000
* situation 1: 0b001
* situation 2: 0b010
* situation 3: 0b011
* situation 4: 0b100
* situation 5: 0b101
* situation 6: 0b110
* situation 7: 0b111
*
* Note: here 'k' represent the last line
*/
for(int k=0; k<STATE_LIMIT; k++){
/*
* dp[1-cur] represent last line
* dp[1-cur][k] not zero, means that the last situation 'k' is an valid situation
*/
if(dp[1-cur][k] != 0){
/*
* check current line's every situation
*/
for(int l=0; l<STATE_LIMIT; l++){
/*
* Note: all legal situations must match 'upline | curline == (STATE_LIMIT)')
* 'k' represent a situation of last line
* 'l' represent a situation of current line
*/
if( ((k|l) == (STATE_LIMIT-1)) && validateLines(k,l, cols)){
dp[cur][l] += dp[1-cur][k];
}
}
}
}
}
return dp[cur][STATE_LIMIT-1];
}
int main(int argc, char *argv[]) {
int n = 4;
int m = 11;
cout<<getCoverWays(n, m)<<endl;
return 0;
}算法的时间复杂度为N*(4^M) , 因为M对时间的影响较大,如果M>N,可以交换二者,确保M的值较小。这样可以提高速度。
2.4 空间压缩
因为只需要用到当前行和上一行的状态,所以只需要两个2^M的数组来保存状态即可
2.5 总结
这是一道经典的状态压缩动态规划问题。本文用整行作为状态来设计动态规划的算法,思路清晰,代码简洁。
本方法时间复杂度较高,还可以通过轮廓线动态规划的方法来进一步优化时间复杂度。
读者可以参考后续的文章 铺瓷砖问题(二)。
[参看]:

