动态规划之变成回文的最小添加次数(转)
本文介绍一下动态规划之变成回文的最小添加次数相关问题。
1. 让字符串变成回文的最少插入次数
1) 对应Leetcode链接
1312. 让字符串成为回文串的最少插入次数 - 力扣(LeetCode)
2) 题目描述
1.1 解题思路
1) 方法1:暴力递归
对应这种回文串问题了一般都是这个范围上的尝试模型,一般都考虑开头和结尾的情况怎么搞:下面我们以abcd为例来分析可能性
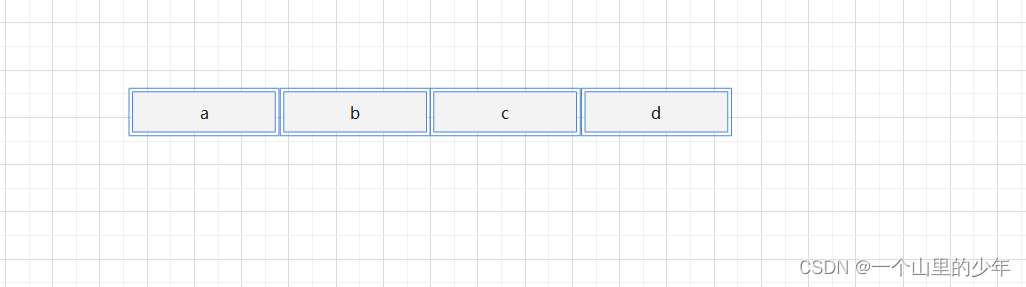
注意:递归含义是字符串从[L…R]范围上变成回文字符串的最小插入代价
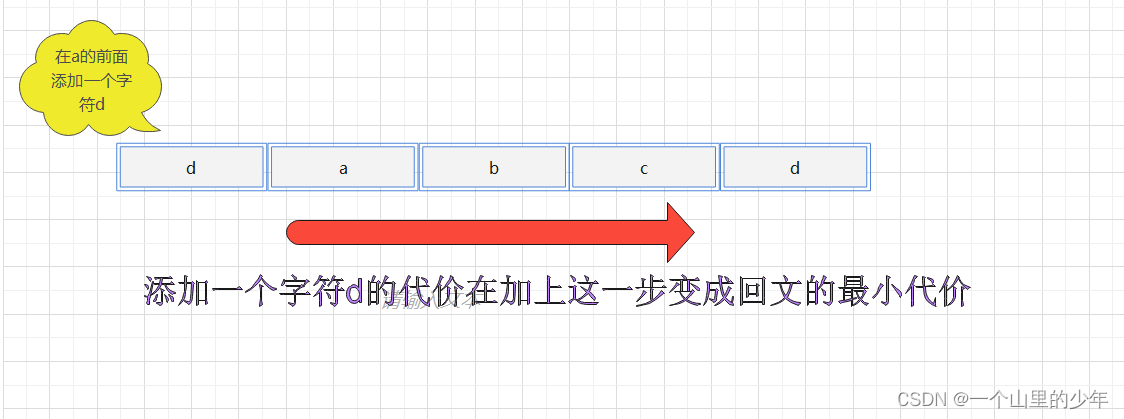
- 可能性1
对应abcd这个字符串我们发现它的开头和结尾不相等,我们可以在a的前面添加一个字符d在加上abc变成回文的最小插入次数:
- 可能性2
在d的后面添加一个字符a:

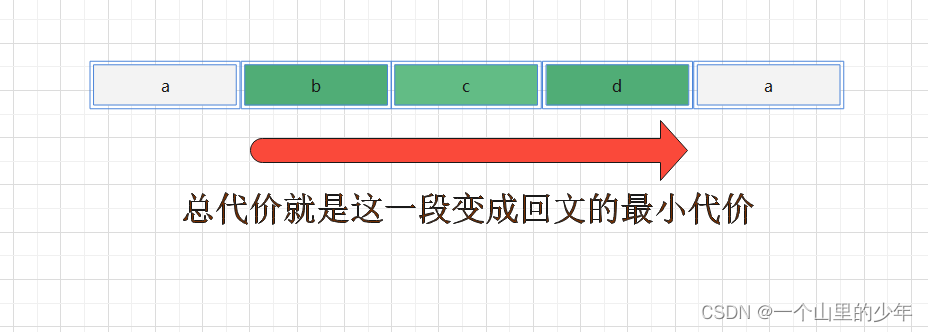
- 可能性3
开头和结尾相等:
相应代码实现如下:
class Solution {
public:
int minInsertions(string s) {
return process(s,0,s.size()-1);
}
//递归含义字符串str从[L.....R]范围变成回文串的最小代价
int process(const string&str,int L,int R)
{
if(L==R)//只有一个字符必然是回文
{
return 0;
}
if(L==R-1)//两个字符如果相等不需要插入不等插入一个即可
{
return str[L]==str[R]?0:1;
}
//可能性1在末尾位置前面插入一个开头字符+[L+1....R]变成回文的最小代价
int ways1=process(str,L+1,R)+1;
//可能性2在开头插入一个末尾字符+[L...R-1]变成回文的最小代价
int ways2=process(str,L,R-1)+1;
//可能性三:开头和结尾相等
int ways3=str[L]==str[R]?process(str,L+1,R-1):INT_MAX;
//三种可能性取最小值
return min(ways1,min(ways2,ways3));
}
};1) 方法2:记忆化搜索
记忆化搜索其实是建立在暴力递归的基础之上,使用辅助空间记录暴力递归重复的过程。下一次再遇到就返回重复计算直接缓存中获取答案。
对应代码:
class Solution {
public:
vector<vector<int>>dp;
int minInsertions(string s) {
dp.resize(s.size(),vector<int>(s.size(),-1));
return process(s,0,s.size()-1);
}
//递归含义字符串str从[L.....R]范围变成回文串的最小代价
int process(const string&str,int L,int R)
{
if(L==R)//只有一个字符必然是回文
{
return 0;
}
if(L==R-1)//两个字符如果相等不需要插入,不等插入一个即可
{
return str[L]==str[R]?0:1;
}
if(dp[L][R]!=-1)
{
return dp[L][R];
}
//可能性1在末尾位置前面插入一个开头字符+[L+1....R]变成回文的最小代价
int ways1=process(str,L+1,R)+1;
//可能性2在开头插入一个末尾字符+[L...R-1]变成回文的最小代价
int ways2=process(str,L,R-1)+1;
//可能性三:开头和结尾相等
int ways3=str[L]==str[R]?process(str,L+1,R-1):INT_MAX;
//三种可能性取最小值
int ans= min(ways1,min(ways2,ways3));
dp[L][R]=ans;//缓存
return ans;
}
};- 方法3:严格位置依赖的动态规划
严格位置依赖的动态规划,其实也是根据暴力递归改过来的。我们可以根据暴力递归的可能性得到状态转移方然后填表即可。
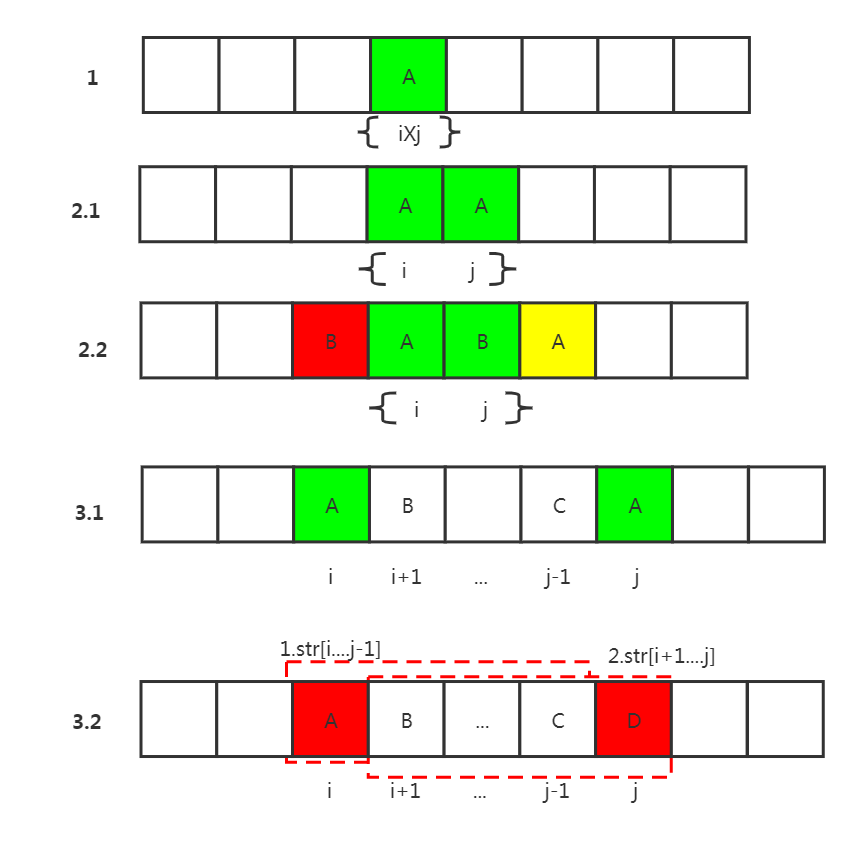
由于前面已经分析过可能性了,在这里就不重复了.
相应代码实现如下:
class Solution {
public:
int minInsertions(string str) {
if(str.size()==1)
{
return 0;
}
int N=str.size();
vector<vector<int>>dp(N,vector<int>(N));
for(int i=0;i<N-1;i++)
{
dp[i][i+1]=str[i]==str[i+1]?0:1;//根据暴力递归的终止条件填的
}
for(int L=N-3;L>=0;L--)
{
for(int R=L+2;R<N;R++)
{
//根据暴力递归的三种可能性得到的状态转移方程
dp[L][R]=min(dp[L+1][R]+1,dp[L][R-1]+1);
if(str[L]==str[R]){
dp[L][R]=min(dp[L][R],dp[L+1][R-1]);
}
}
}
return dp[0][N-1];
}
//递归含义字符串str从[L.....R]范围变成回文串的最小代价
/*int process(const string&str,int L,int R)
{
if(L==R)//只有一个字符必然是回文
{
return 0;
}
if(L==R-1)//两个字符如果相等不需要插入不等插入一个即可
{
return str[L]==str[R]?0:1;
}
if(dp[L][R]!=-1)
{
return dp[L][R];
}
//可能性1在末尾位置前面插入一个开头字符+[L+1....R]变成回文的最小代价
int ways1=process(str,L+1,R)+1;
//可能性2在开头插入一个末尾字符+[L...R-1]变成回文的最小代价
int ways2=process(str,L,R-1)+1;
//可能性三:开头和结尾相等
int ways3=str[L]==str[R]?process(str,L+1,R-1):INT_MAX;
//三种可能性取最小值
int ans= min(ways1,min(ways2,ways3));
dp[L][R]=ans;//缓存
return ans;
}*/
};2. 让字符串变成回文的最少插入次数并返回一个结果
1) 对应OJ链接
添加最少的字符让字符串变为回文字符串(1)_牛客题霸_牛客网 (nowcoder.com)
2) 题目描述
3) 解题思路
可能老铁看到这个问题的时候直接傻眼了这改怎么做啊?其实这个问题是可以根据我们上一问的dp表来解决的,我们可以利用dp表回溯回去。根据dp表的告诉我们的答案确定最终字符串的长度。步骤如下:
1.从我们得到答案的位置开始回溯,判断当前位置是来自那种可能性进行还原。 2.如果dp[L][R]==dp[L+1][R]说明是可能在字符串的末尾位置添加了开头的字符。 3.如果dp[L][R]==dp[L][R-1]说明可能是在字符串的开头添加了结尾字符。 4.根据上面的步骤我们就可以还原出一个字符串了,具体请看代码。
4) 对应代码
#include<iostream>
#include<vector>
#include<string>
using namespace std;
int main() {
string str;
cin >> str;
int N = str.size();
vector<vector<int>>dp(N, vector<int>(N));
//默认dp的每个位置初始化为0;
for (int i = 0; i < N - 1; i++) {
dp[i][i + 1] = str[i] == str[i + 1] ? 0 :1; //根据暴力递归的终止条件填的
}
for (int L = N - 3; L >= 0; L--) {
for (int R = L + 2; R < N; R++) {
//根据暴力递归的三种可能性得到的状态转移方程
dp[L][R] = min(dp[L + 1][R] + 1, dp[L][R - 1] + 1);
if (str[L] == str[R]) {
dp[L][R] = min(dp[L][R], dp[L + 1][R - 1]);
}
}
}
//---------------------------------------------------//
//前面和上题的过程一模一样下面是根据dp表还原所有可能性
int L = 0;//最左上脚进行回溯
int R = N - 1;
string ans(str.size()+dp[L][R],'/0');//肯能结果字符串的长度
int ansL=0;
int ansR=ans.size()-1;
while(L<R)
{
if(dp[L][R]==dp[L][R-1]+1)
{
ans[ansL++]=str[R];
ans[ansR--]=str[R--];
}
else if(dp[L][R]==dp[L+1][R]+1)
{
ans[ansL++]=str[L];
ans[ansR--]=str[L++];
}
else //可能性三开头和结尾相等
{
ans[ansL++]=str[L++];
ans[ansR--]=str[R--];
}
}
if(L==R)//有可能最后还剩下一个字符
{
ans[ansL]=str[R];
}
cout<<ans<<endl;
return 0;
}5) 扩展: 如果我们要求得所有的结果又该怎么做了?
如果我们想要获得所有结果我们需要进行回溯,枚举所有的可能性。具体请看代码。
#include<iostream>
#include<vector>
#include<string>
using namespace std;
//当前来到dp表中的(L,R)位置
//从path[pL......pR].....
void process(const string& str, vector<vector<int>>& dp, int L, int R, string& path, int pL, int pR, vector<string>& ans)
{
if (L >= R)//如果L>R说明直接的过程已经将paht填满了
{
if (L == R)//还剩下一个字符
{
path[pL] = str[L];
}
ans.push_back(path);//收集所有的答案
return;
}
else
{
if (dp[L][R] == dp[L][R - 1]+1)//如果答案可以来自我的左侧
{
path[pL] = str[R];
path[pR] = str[R];
process(str, dp, L, R - 1, path, pL + 1, pR - 1, ans);
}
if (dp[L][R] == dp[L + 1][R] + 1)//如果答案可以来自我的下方
{
path[pL] = str[L];
path[pR] = str[L];
process(str, dp, L + 1, R, path, pL+1,pR-1, ans);
}
if (str[L] == str[R] && (L == R - 1 || dp[L+1][R - 1] == dp[L][R]))
{
path[pL] = str[L];
path[pR] = str[R];
process(str, dp, L + 1, R-1, path, pL + 1, pR - 1, ans);
}
}
}
int main() {
string str;
cin >> str;
int N = str.size();
vector<vector<int>>dp(N, vector<int>(N));
//默认dp的每个位置初始化为0;
for (int i = 0; i < N - 1; i++) {
dp[i][i + 1] = str[i] == str[i + 1] ? 0 :1; //根据暴力递归的终止条件填的
}
for (int L = N - 3; L >= 0; L--) {
for (int R = L + 2; R < N; R++) {
//根据暴力递归的三种可能性得到的状态转移方程
dp[L][R] = min(dp[L + 1][R] + 1, dp[L][R - 1] + 1);
if (str[L] == str[R]) {
dp[L][R] = min(dp[L][R], dp[L + 1][R - 1]);
}
}
}
vector<string>ans;
string path;
path.resize(str.size() + dp[0][N - 1]);
process(str, dp, 0, N - 1, path, 0, str.size() + dp[0][N - 1] - 1,ans);
for (int i = 0; i < ans.size(); i++)
{
cout << ans[i] << endl;
}
return 0;
}
[参看]:

