动态规划背包问题(转)
本文介绍一下动态规划之背包问题。
1. 前言
本文主要介绍常见的四种背包问题,思维导图如下:
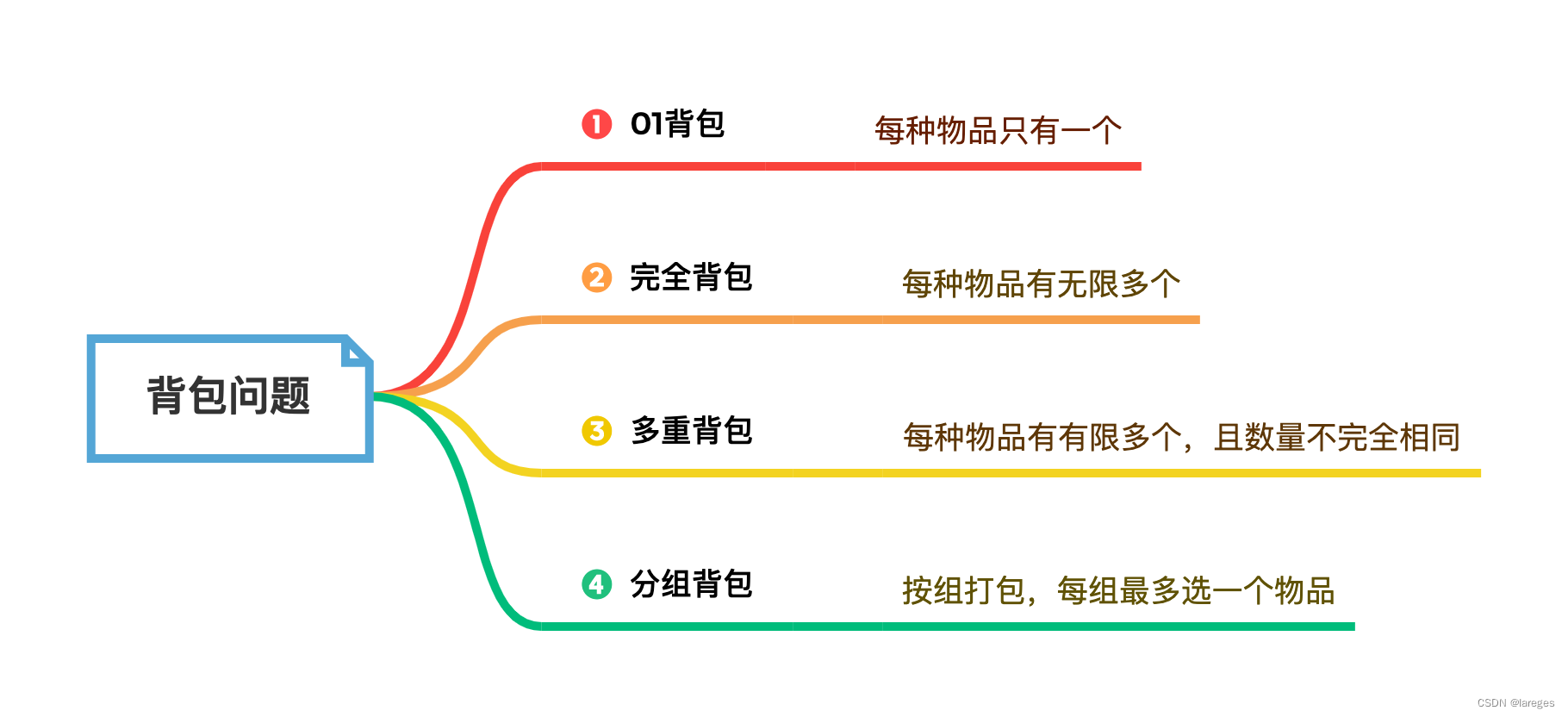
2 01背包
现有N件物品和一个最多能承重M的背包,第i件物品的重量是$w_i$,价值是$v_i$。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。
因为每件物品只有选与不选两种状态,所以该问题又称01背包问题。
设dp[i][j]的含义是: 在背包承重为j的前提下,从前i个物品中选能够得到的最大价值。不难发现dp[N][M]就是本题的答案。
如何计算dp[i][j]呢?我们可以将它划分为以下两部分:
-
选第i个物品: 由于第i个物品一定会被选择,那么相当于从前
i-1个物品中选且总重量不超过j-w[i],对应dp[i-1][j-w[i]] + v[i] -
不选第i个物品: 意味着从前
i-1个物品中选且总重量不超过j, 对应dp[i-1][j]
结合以上两点可得递推公式:
$ dp[i][j] = max(dp[i−1][j],dp[i−1][j−w[i]]+v[i]) $
由于下标不能是负数,所以上述递推公式要求$j \ge w[i]$。当$j \lt w[i]$时,意味着第i个物品无法装进背包, 此时dp[i][j]=dp[i-1][j]。综合以上可以得出:
$ dp[i][j] = \begin{cases} dp[i-1][j], \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad j<w[i] \\ max(dp[i-1][j], dp[i-1][j-w[i]] + v[i]), \qquad j \ge w[i] \end{cases} $
dp数组应当如何初始化呢?当背包承重为0时,显然装不下任何物品,所以$dp[i][0]=0 \;(1 \leq i \leq N)$; 若一个物品也不选(即从前0个物品中选),此时最大价值也是0,所以$dp[0][j]=0 \; (0 \leq j\leq M)$。由此可知, dp数组应当全0初始化,即声明为全局变量。
题目链接: AcWing 2. 01背包问题
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int w[N], v[N];
int dp[N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (j < w[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
cout << dp[n][m] << "\n";
return 0;
}时间复杂度为$O(mn)$。
1.1 使用滚动数组优化
之前我们用到的dp数组是二维数组,它可以进一步优化成一维数组。
观察递推公式不难发现,dp数组中第i行的元素仅由第i-1行的元素得来,即第0行元素的更新值放到第1行,第1行元素的更新值放到第2行,以此类推。与其把一行的更新值放到新的一行,不如直接就地更新,因此我们的dp数组只需要一行来存储,即一维数组。
去掉dp数组的第一维后,递推公式变成:
$ dp[j] = \begin{cases} dp[j], \qquad \quad \qquad \qquad \qquad \qquad \qquad j<w[i] \\ max(dp[j], dp[j-w[i]] + v[i]), \qquad j \ge w[i] \end{cases} $
原先j是从1遍历至m的,现在只需从w[i] 遍历至m。但,这个遍历顺序真的对吗?
请看下图:
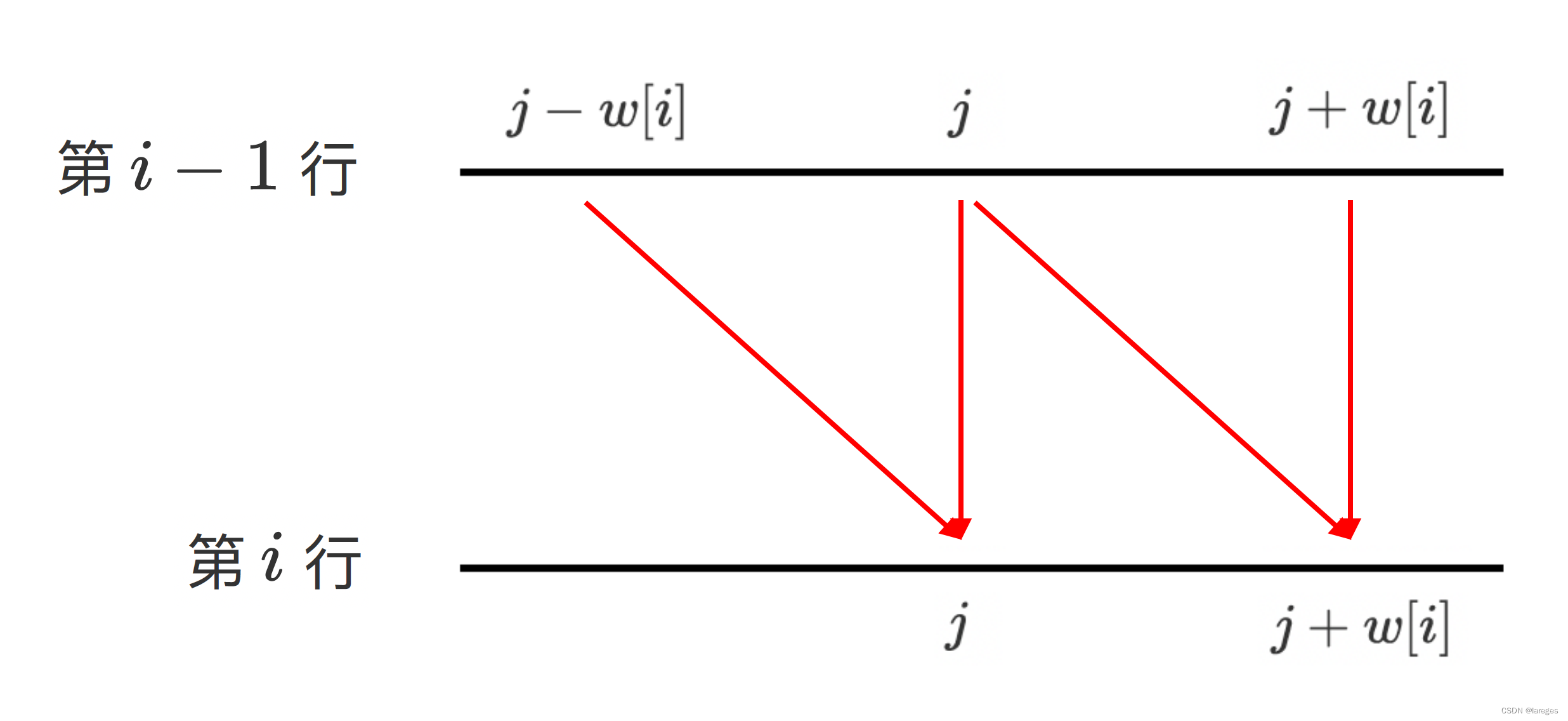
红色箭头表示,在二维数组中,$dp[i][j]$由$dp[i-1][j-w[i]]和dp[i-1][j]$得来,$dp[i][j+w[i]]$由$dp[i−1][j]$和$dp[i−1][j+w[i]]$得来。用一维数组的话来讲就是,第i行的$dp[j]$由第i-1行的$dp[j−w[i]]$和$dp[j]$得来,第i行的$dp[j+w[i]]$由第i-1行的$dp[j]$和$dp[j+w[i]]$得来。
如果j从小到大遍历,那么会先更新$dp[j]$, 再更新$dp[j+w[i]]$,这就导致在更新$dp[j+w[i]]$时使用的是第i行的$dp[j]$而非第i-1行的dp[j],即当j从小到大遍历时,二维数组的递推式变成了:
$ dp[i][j] = \begin{cases} dp[i-1][j], \qquad \qquad \qquad \qquad \qquad \qquad \qquad j<w[i] \\ max(dp[i-1][j], dp[i][j-w[i]] + v[i]), \qquad j \ge w[i] \end{cases} $
PS: 请牢记该式,后续讲解完全背包时会提到它。
这显然是错误的。事实上,让j从大到小遍历就不会出现这个问题。
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int w[N], v[N];
int dp[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];
for (int i = 1; i <= n; i++)
for (int j = m; j >= w[i]; j--)
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
cout << dp[m] << "\n";
return 0;
}当然,w数组和v数组也是不必要的,我们可以边输入边处理,因此可以得到01背包问题的最终版代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dp[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int w, v;
cin >> w >> v;
for (int j = m; j >= w; j--)
dp[j] = max(dp[j], dp[j - w] + v);
}
cout << dp[m] << "\n";
return 0;
}到此为止,可以总结出,当dp数组是二维数组时,j既可以从小到大遍历也可以从大到小遍历,但当dp数组是一维数组时,j只能从大到小遍历。
2. 完全背包问题
现有N种物品和一个最多能承重M的背包,每种物品都有无限个,第i种物品的重量是$w_i$, 价值是$v_i$。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值
设dp[i][j]的含义是:在背包承重为j的前提下,从前i种物品中选能够得到的最大价值。
如何计算dp[i][j] 呢?我们可以将它划分为以下若干部分:
-
选0个第i种物品:相当于不选第i种物品,对应dp[i−1][j]
-
选1个第i种物品:对应dp[i−1][j−w[i]]+v[i]。
-
选2个第i种物品:对应$dp[i-1][j-2\cdot w[i]]+2\cdot v[i]$
-
…
上述过程并不会无限进行下去,因为背包承重是有限的。设第i种物品最多能选t个,于是可知$t=\lfloor \frac{j}{w[i]}\rfloor$ 从而得到递推式:
$ dp[i][j]=\max_{0 \le k \le t} dp[i-1][j - k\cdot w[i]] + k \cdot v[i] $
题目链接:AcWing 3. 完全背包问题
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int w[N], v[N];
int dp[N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
int t = j / w[i];
for (int k = 0; k <= t; k++)
dp[i][j] = max(dp[i][j], dp[i - 1][j - k * w[i]] + k * v[i]);
}
cout << dp[n][m] << "\n";
return 0;
}若将t的值改为$\min(1,\,j/w[i])$,则完全背包将退化为01背包。
上述代码的时间复杂度为$O(m^2\sum_iw_i^{-1})\approx O(m^2n)$, TLE是必然的。
2.1 使用滚动数组优化
考虑$dp[i][j]$,此时第i种物品最多能选$t_1=\lfloor \frac{j}{w[i]}\rfloor$个,将递推公式展开:
$ dp[i][j]=max(dp[i-1][j], dp[i-1][j-w[i]]+v[i], dp[i-1][j-2 \cdot w[i]] + 2 \cdot v[i], \cdot \cdot \cdot ,dp[i-1][j - t_1 \cdot w[i]] + t_1 \cdot v[i]) $
下面考虑$dp[i][j-w[i]]$,此时第i种物品最多能选$t_2=\lfloor \frac{j-w[i]}{w[i]}\rfloor = \lfloor \frac{j}{w[i]} - 1\rfloor = t_1 - 1$个,相应的递推公式为:
$ dp[i][j-w[i]]=max(dp[i-1][j-w[i]], dp[i-1][j-w[i]-w[i]]+v[i], dp[i-1][j-w[i]-2 \cdot w[i]]+2 \cdot v[i], \cdot \cdot \cdot ,dp[i-1][j -w[i] - t_2 \cdot w[i]] + t_2 \cdot v[i]) $ 又注意到$t_1=t_2+1$,上式可化简为:
$ dp[i][j-w[i]]=max(dp[i-1][j-w[i]], dp[i-1][j-2 \cdot w[i]] + v[i], dp[i-1][j-3 \cdot w[i]] + 2 \cdot v[i], \cdot \cdot \cdot , dp[i-1][j-t_1 \cdot w[i]] + (t_1 -1)\cdot v[i]) $
将该式与$dp[i][j]$的递推式比较不难发现:
$ dp[i][j]=max(dp[i-1][j], dp[i][j-w[i]]+v[i]) $
根据1.1节中的结论,该式对应的是j从小到大遍历,于是我们只需把01背包问题的代码中的j改为从小到大遍历即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dp[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int w, v;
cin >> w >> v;
for (int j = w; j <= m; j++) // 只需修改这一行
dp[j] = max(dp[j], dp[j - w] + v);
}
cout << dp[m] << "\n";
return 0;
}优化后的时间复杂度为$O(nm)$。
3. 多重背包
现有N种物品和一个最多能承重M的背包,第i种物品的数量是$s_i$, 重量是$w_i$,价值是$v_i$。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。
回顾完全背包问题的暴力解法,在背包承重为j的前提下,第i种物品最多能放$t=j/w[i]$个(这里是整除)。而在01背包问题中,第i种物品只有一个,所以应当取$t=\min(1,\,j/w[i])$。由此可见,对于多重背包问题,只需取$t=\min(s[i],\,j/w[i])$。
对完全背包问题的暴力解法做一点简单修改即可求解多重背包问题。
题目链接:AcWing 4. 多重背包问题
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int dp[N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int w, v, s;
cin >> w >> v >> s;
for (int j = 1; j <= m; j++) {
int t = min(s, j / w); // 只有这里需要修改
for (int k = 0; k <= t; k++)
dp[i][j] = max(dp[i][j], dp[i - 1][j - k * w] + k * v);
}
}
cout << dp[n][m] << "\n";
return 0;
}时间复杂度为$O(m\sum_i s_i)$,但还可以进一步优化
3.1 使用二进制优化
从时间复杂度的表达式可以看出,O(m)的部分已经无法再优化了,我们只能从$O(\sum_i s_i)$入手。
先来看一个例子。水果店里有 40 40 40 个苹果,小明计划购买$n(1\leq n\leq 40)$个苹果,试问如何让小明尽可能快速地完成购买?一个显而易见的暴力做法是,让小明一个个拿(单位是个),但效率过于低下。事实上,店员可事先准备好6个箱子,每个箱子中的苹果数量分别为$[1,2,4,8,16,9]$,再让小明按箱子拿(单位是箱子),无论小明计划购买多少个,他最多只需要拿6次,而在暴力做法中,小明最多需要拿40次。
下面用数学语言来描述上面的例子。对于任意的正整数s,我们都可以找到$\lfloor \log_2 s\rfloor+1\triangleq k$个正整数$a_1,\cdots, a_k$,使得$\forall\, n\in[0,s]$都有
$ n=v^Ta, \quad a=(a_1,\cdots, a_k)^T, \quad a_i=\begin{cases} 2^{i-1}, \qquad \quad \qquad \qquad \qquad \qquad 1 \le i \le k-1 \\ s-2^{k-1}+1(\in [1, 2^{k-1}]), \qquad i=k \end{cases} $
其中$v=(v_1,\cdots,v_k)^\mathrm{T}$,且其分量非0即1。
感兴趣的读者可自行证明,这里不再赘述。回到本题,先不考虑背包的承重,我们在暴力求解多重背包的时候,对于每种物品i,都要从0逐个枚举至s[i],效率无疑是低下的。现在,对于每种物品i,我们将这s[i]个物品分散至$\lfloor \log_2 s[i]\rfloor+1$个「箱子」中,于是多重背包便化成了01背包。
题目链接:AcWing 5. 多重背包问题 II
多重背包问题中的一个「箱子」相当于01背包问题中的一件「物品」,因此我们需要估计出多重背包问题中到底有多少个箱子。显然箱子总数为:
$ N=\sum_{i=1}{n}{(\lfloor \log_2{s[i]}+1 \rfloor)} \le sum_{i=1}{n}{\lfloor \log_2{2000} \rfloor} + n = 11n \le 11000 $
#include <bits/stdc++.h>
using namespace std;
const int N = 11010, M = 2010;
int w[N], v[N];
int dp[M];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
int cnt = 0;
while (n--) {
int a, b, s; // a是重量, b是价值, c是数量
cin >> a >> b >> s;
for (int k = 1; k <= s; k *= 2) {
cnt++;
w[cnt] = a * k, v[cnt] = b * k;
s -= k;
}
if (s > 0) {
cnt++;
w[cnt] = a * s, v[cnt] = b * s;
}
}
n = cnt;
for (int i = 1; i <= n; i++)
for (int j = m; j >= w[i]; j--)
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
cout << dp[m] << "\n";
return 0;
}优化后的时间复杂度为$O(m\sum_i \log s_i)$。
4. 分组背包
现有N组物品和一个最多能承重M的背包,每组物品有若干个,同一组内的物品最多只能选一个。每件物品的重量是$w_{ij}$, 价值是$v_{ij}$,其中i是组号,j是组内编号。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。
设$dp[i][j]$的含义是:在背包承重为j的前提下,从前i组物品中选能够得到的最大价值。
如何计算$dp[i][j]$呢?我们可以将它划分为以下若干部分:
-
不选第i组的物品:对应$dp[i-1][j]$
-
选第i组的第1个物品:对应$dp[i-1][j-w[i][1]]+v[i][1]$
-
选第1组的第2个物品: 对应$dp[i-1][j-w[i][2]]+v[i][2]$
-
$\cdots$
-
选第i组的第s[i]个物品:对应$dp[i-1][j-w[i][s[i]]]+v[i][s[i]]$。
直接将dp数组优化到一维可得递推式:
$ dp[j]=\max(dp[j], \max_{1 \le k \le s[i]}{dp[j-w[i][k]]+v[i][k]}) $
题目链接:AcWing 9. 分组背包问题
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int w[N][N], v[N][N], s[N];
int dp[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> s[i];
for (int j = 1; j <= s[i]; j++)
cin >> w[i][j] >> v[i][j];
}
for (int i = 1; i <= n; i++)
for (int j = m; j >= 1; j--)
for (int k = 1; k <= s[i]; k++)
if (j >= w[i][k])
dp[j] = max(dp[j], dp[j - w[i][k]] + v[i][k]);
cout << dp[m] << "\n";
return 0;
}5. 总结
我们可以用一个公式来表示01背包、完全背包和多重背包:
$ dp[i][j]=\max_{0 \le k \le t}{dp[i-1][j-k\cdot w[i]] + k\cdot v[i]}, \qquad \qquad \qquad t=\begin{cases} \min(1, j/w[i]), \qquad \qquad \qquad \qquad 01背包 \\ \min(+\infty, j/w[i])=j/w[i], \qquad 完全背包 \\ \min(s[i], j/w[i]), \qquad \qquad \qquad \quad 多重背包 \end{cases} $
[参看]:

