数据结构图的连通性问题
在这一节中,我们将利用遍历图的算法来求解图的连通性问题,并讨论:
-
最小代价
生成树 -
重连通性与通信网络的经济性和可靠性的关系
1. 无向图的连通分量和生成树
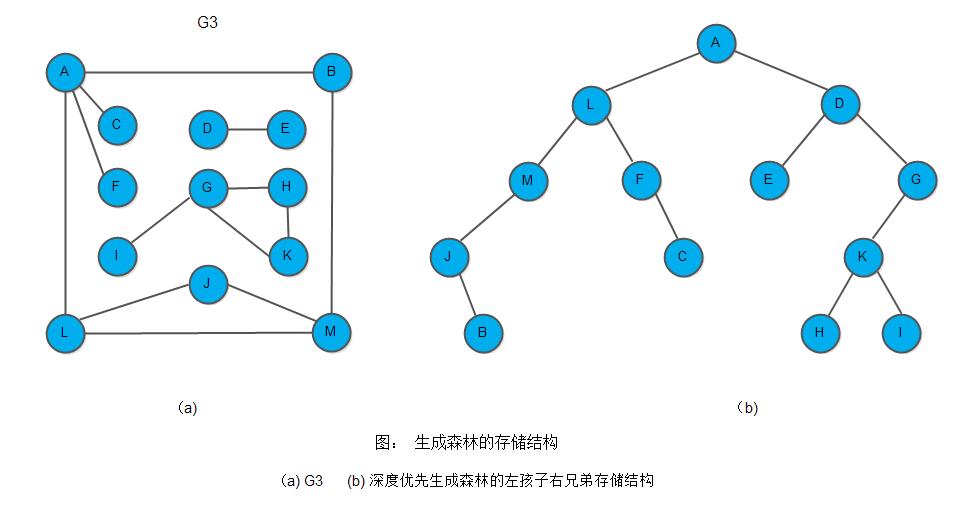
在对无向图进行遍历时,对于连通图,仅需从图中任一顶点出发,进行深度优先搜索或广度优先搜索,便可访问到图中所有顶点。对非连通图,则需从多个顶点出发进行搜索,而每一次从一个新的起始点出发进行搜索过程中得到的顶点访问序列恰为其各个连通分量中的顶点集。例如,下图中G3是非连通图,按照其邻接表(图(b))进行深度优先搜索遍历,3次调用DFS过程(分别从顶点A、D和G出发)得到的顶点访问序列为:
A L M J B F C D E G K H I
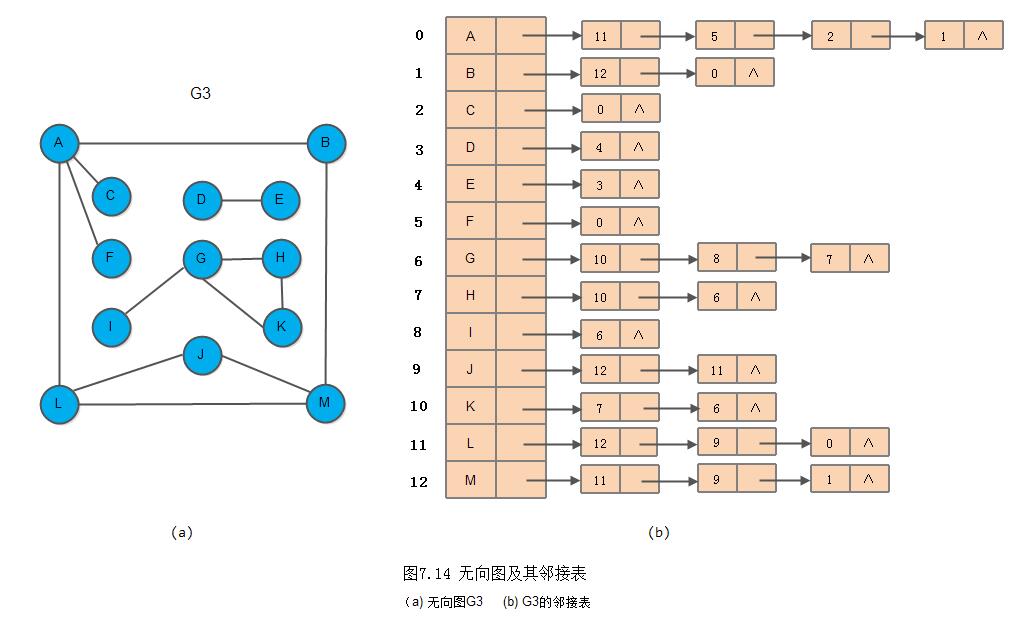
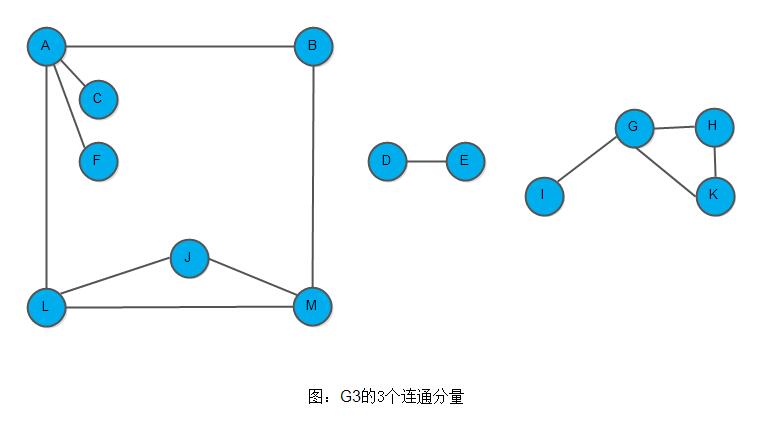
这3个顶点集分别加上所有依附于这些顶点的边,边构成了非连通图G3的3个连通分量,见如下图:
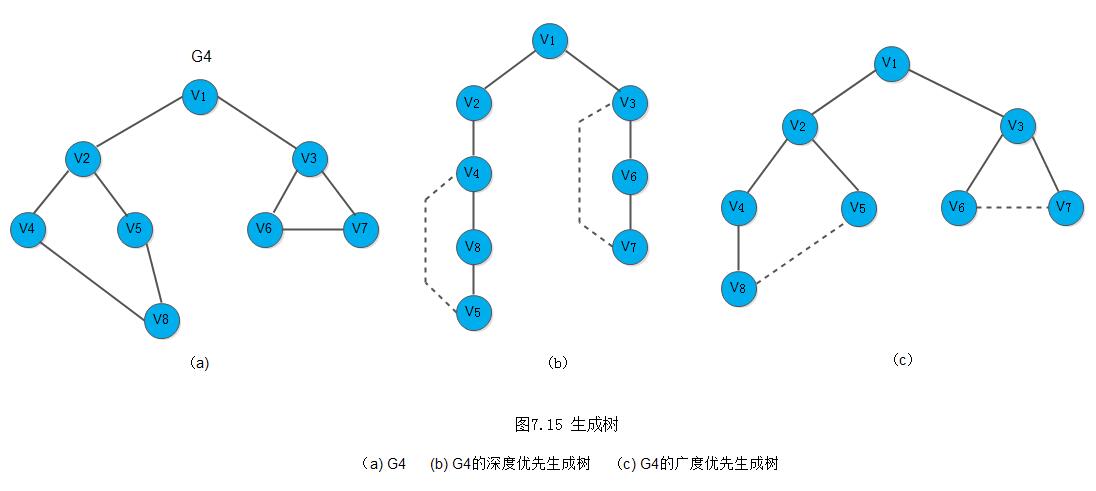
设E(G)为连通图G中所有边的集合,则从图中任一顶点出发遍历图时,必定将E(G)分成两个集合T(G)和B(G),其中T(G)是遍历图过程中经历的边的集合;B(G)是剩余的边的集合。显然,T(G)和图G中所有顶点一起构成连通图G的极小连通子图。按照图的定义和术语一节中的定义,它是连通图的一棵生成树,并且称由深度优先搜索得到的为深度优先生成树;由广度优先搜索得到的为广度优先生成树。例如,下图7.15(b)和(c)所示分别为连通图G4的深度优先生成树和广度优先生成树,图中虚线为集合B(G)中的边。
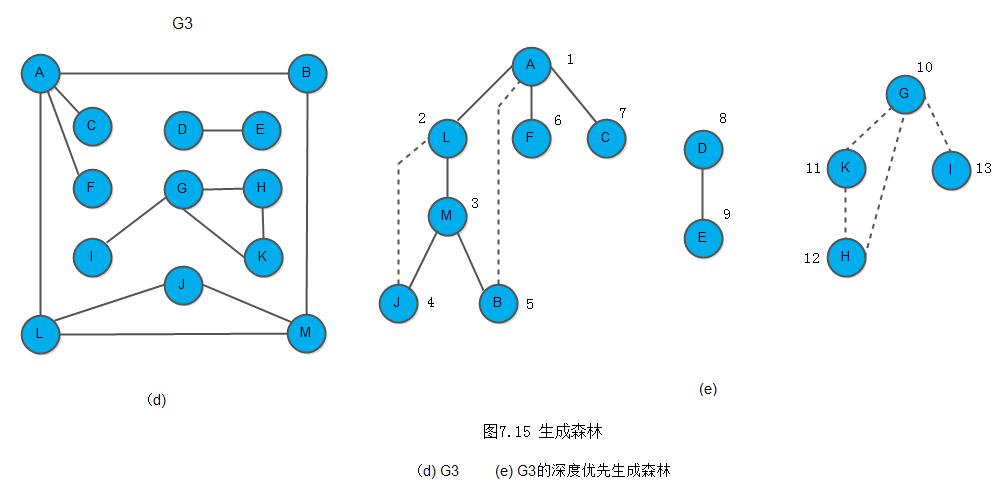
对于非连通图,每个连通分量中的顶点集,和遍历时走过的边一起构成若干棵生成树,这些连通分量的生成树组成非连通图的生成森林。如下图7.15(e)所示为G3的深度优先生成森林,它由三棵深度优先生成树组成。
假设以孩子兄弟链表作为生成森林的存储结构,则算法7.7生成非连通图的深度优先森林,其中DFSTree函数如算法7.8所示。显然,算法7.7的时间复杂度和遍历相同。
算法7.7:
void DFSForest(Graph G, CSTree &T){
//建立无向图G的深度优先生成森林的(最左)孩子(右)兄弟链表T
T = NULL;
for(v = 0; v < G.vexnum; v++)
visited[v] = FALSE;
for(v = 0; v < G.vexnum; v++){
if(!visited[v]){
p = (CSTree)malloc(sizeof(CSNode)); //分配跟节点
*p = {GetVex(G, v), NULL, NULL}; //给该节点赋值
if(!T){
T = p; //是第一棵生成树的根(T的根)
}else{
q->nextsibling = p; //是其他生成树的根(前一棵的根的"兄弟")
}
q = p; //q指示当前生成树的根
DFSTree(G, v, p); //建立以p为根的生成树
}
}
}算法7.8:
void DFSTree(Graph G, int v, CSTree &T){
//从第v个顶点出发,深度优先遍历图G,建立以T为根的生成树
visited[v] = TRUE;
first = TRUE;
for(w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w)){
if(!visited[w]){
p = (CSTree)malloc(sizeof(CSNode)); //分配孩子节点
*p = {GetVex(G, w), NULL, NULL};
if(first){ //w是v的第一个未被访问的邻接顶点
T->lchild = p; first = FALSE; //是根的左孩子节点
}else{ //w是v的其他未被访问的邻接顶点
q->nextsibling = p; //是上一邻接顶点的右兄弟节点
}
q = p;
DFSTree(G, w, q); //从第w个顶点出发深度优先遍历图G,建立子生成树q
}
}
}如下是对无向图G3的深度优先生成森林的孩子兄弟链表结构:
2. 有向图的强连通分量
深度优先搜索是求有向图的强连通分量的一个新的有效方法。假设以十字链表作有向图的存储结构,则求强连通分量的步骤如下:
1) 在有向图G上,从某个顶点出发沿以该顶点为尾的弧进行深度优先搜索遍历,并按其所有邻接点的搜索都完成(即退出DFS函数)的顺序将顶点排列起来。此时需对7.3.1中的算法(即深度优先搜索算法)做如下两点修改:
-
在进入DFSTraverse函数时,首先进行计数变量的初始化,即在入口处加上count=0的语句;
-
在退出DFS函数之前将完成搜索的顶点号记录在另一个辅助数组finished[vexnum]中,即在DFS函数结束之前加上finished[++count]=v的语句
进行修改后的函数如下所示:
Boolean visited[MAX]; //访问标志数组
Status (*VisitFunc)(int v); //函数变量
int count;
int finished[MAX];
//对图G作深度优先遍历
void DFSTraverse(Graph G, Status (*Visit)(int v))
{
VisitFunc = Visit; //使用全局变量VisitFunc,使DFS不必设函数指针参数
count = 0; //将当前完成搜索的技术置为0
//访问标志数组初始化
for(v = 0; v < G.vexnum; v++)
visited[v] = FALSE;
for(v = 0; v < G.vexnum; v++)
{
if(!visited[v])
DFS(G, v); //对尚未访问的顶点调用DFS
}
}
//从第v个顶点出发递归地深度优先遍历图G
void DFS(Graph G, int v)
{
visited[v] = TRUE;
VisitFunc(v); //访问第v个顶点
for(w = FirstAdjVex(G, v); v >= 0; w = NextAdjVex(G, v, w))
{
if(!visited[w])
DFS(G, w); //对v的尚未访问的邻接顶点w递归调用DFS
}
finished[count++] = v; //按逆序记录当前已经搜索完的顶点(注: 这里应该是count++, 而不是++count)
}2) 在有向图G上,从最后完成搜索的顶点(即finished[vexnum -1])中的顶点)出发,沿着以该顶点为头的弧作逆向的深度优先搜索遍历,若此次遍历不能访问到有向图中所有顶点,则从余下的顶点中最后完成搜索的那个顶点出发,继续作逆向的深度优先搜索遍历,依次类推,直至有向图中所有顶点都被访问到为止。此时调用DFSTraverse时主要作如下修改:函数中第二个循环语句的边界条件应改为v从finished[vexnum-1]至finished[0]。
进行修改后的函数如下所示:
Boolean visited[MAX]; //访问标志数组
Status (*VisitFunc)(int v); //函数变量
int count;
int finished[MAX];
//对图G作深度优先遍历
void DFSTraverse(Graph G, Status (*Visit)(int v))
{
VisitFunc = Visit; //使用全局变量VisitFunc,使DFS不必设函数指针参数
//访问标志数组初始化
for(v = 0; v < G.vexnum; v++)
visited[v] = FALSE;
for(i = G.vexnum -1; i >= 0;i--)
{
v = finished[i];
if(!visited[v])
DFS(G, v); //对尚未访问的顶点调用DFS
}
}
//从第v个顶点出发递归地深度优先遍历图G
void DFS(Graph G, int v)
{
visited[v] = TRUE;
VisitFunc(v); //访问第v个顶点
for(w = FirstAdjVex(G, v); v >= 0; w = NextAdjVex(G, v, w))
{
if(!visited[w])
DFS(G, w); //对v的尚未访问的邻接顶点w递归调用DFS
}
}由此,每一次调用DFS作逆向深度优先遍历所访问到的顶点集便是有向图G中一个强连通分量的顶点集。
例如,图7.11(即下图)所示的有向图,假设从顶点V1出发作深度优先搜索遍历,得到finished数组中的顶点号为{1,3,2,0};则再从顶点V1出发作逆向的深度优先搜索遍历,得到两个顶点集{V1, V3, V4}和{V2},这就是该有向图的两个强连通分量的顶点集。

上述求强连通分量的第二步,其实质为: 1) 构造一个有向图Gr,设G=(V, {A}),则Gr=(V,{Ar}),对于所有<vi,vj>∈A,必有<vj,vi>∈Ar。即Gr中拥有和G方向相反的弧;2) 在有向图Gr上,从顶点finished[vexnum-1]出发作深度优先搜索遍历。可以证明,在Gr上所得深度优先生成森林中每一颗树的顶点集即为G的强连通分量的顶点集。
显然,利用遍历求强连通分量的时间复杂度亦和遍历相同。
3. 最小生成树
假设要在n个城市之间建立通信联络网,则连通n个城市只需要n-1条线路。这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?
可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋予边的权值表示相应的代价。对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。现在,我们要选择这样一棵生成树,也就是使总的耗费最少。这个问题就是构造连通网的最小代价生成树(Minimum Cost Spanning Tree)(简称最小生成树)的问题。一棵生成树的代价就是树上各边的代价之和。
构造最小生成树可以有多种方法。其中多数方法利用了最小生成树的下列一种简称为MST的性质: 假设N=(V, {E})是一个连通网,U是顶点集V的一个非空子集。若(u,v)是一条具有最小权值(代价)的边,其中u∈U, v∈V-U,则必存在一棵包含边(u,v)的最小生成树。
可以用反证法证明之。假设网N的任何一棵最小生成树都不包含(u, v)。设T是连通网上的一棵最小生成树,当将边(u,v)加入到T中时,由生成树的定义,T中必存在一条包含(u,v)的回路。另一方面,由于T是生成树,则在T上必存在另一条边(u',v'),其中 u'∈U,v'∈V-U,且u和u'之间,v和v'之间均有路径相通。删去边(u',v'),便可消除上述回路,同时得到另一棵生成树T'。因为(u,v)的代价不高于(u’,v’),则T'的代价亦不高于T,T'是包含(u,v)的一棵最小生成树。由此和假设矛盾。
普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法是两个利用MST性质构造最小生成树的算法。
下面先介绍普里姆算法。
假设N=(V,{E})是连通网,TE是N上最小生成树中边的集合。算法从$U={u_0}(u_0∈V)$, TE={}开始,重复执行下述操作: 在所有u∈U,v∈V-U的边(u,v)∈E中找一条代价最小的边$(u_0,v_0)$并入集合TE,同时$v_0$并入U,直至U=V为止。此时TE中必有n-1条边,则T=(V, {TE})为N的最小生成树。
为实现这个算法需附设一个辅助数组closedge,以记录从U到V-U具有最小代价的边。对每个顶点vi ∈ V-U,在辅助数组中存在一个相应的分量closedge[i-1],它包括两个域,其中lowcost存储该边上的权。显然:
closedge[i-1].lowcost = Min{cost(u, v) | u ∈ U}
注: cost(u,v)表示赋予边(u,v)的权
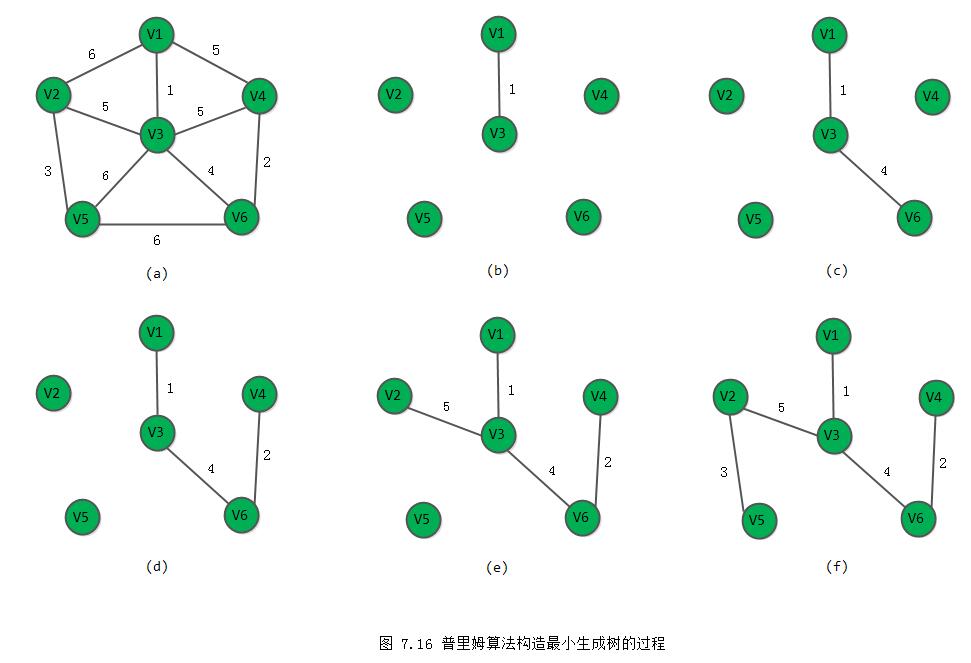
vex域存储该边依附的在U中的顶点。例如,上图(图7.16)所示为按普里姆算法构造网的一棵最小生成树的过程,在构造过程中辅助数组中各分量值的变化如图7.17所示。初始状态时,
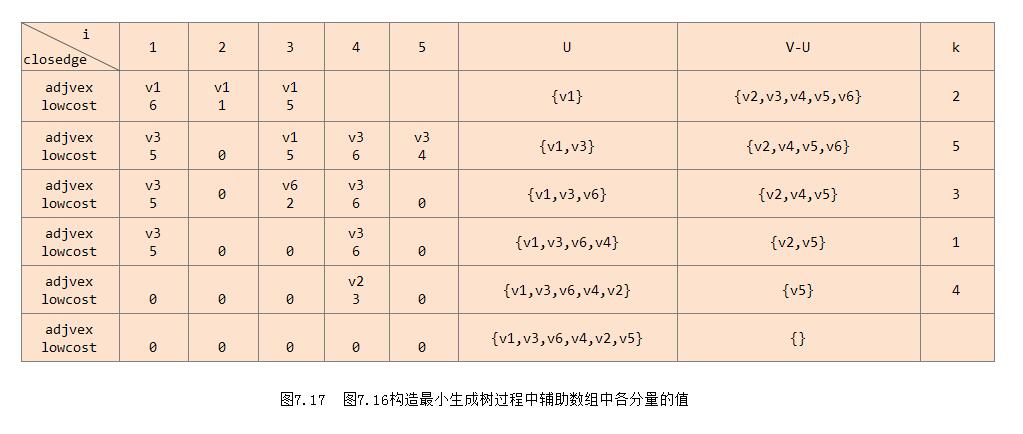
由于U={v1},则到V-U中各顶点的最小边,即为从依附于顶点1的各条边中,找到一条代价最小的边(u0,v0)=(1,3)为生成树的第一条边,同时将v0(=v3)并入集合U。然后修改辅助数组中的值。首先将closedge[2].lowcost改为0,以示顶点v3已并入U。然后,由于边(v3,v2)上的权值小于closedge[1].lowcost,则需修改closedge[1]为边(v3,v2)及其权值。同理修改closedge[4]和closedge[5]。依次类推,直到U=V。假设以二维数组表示网的邻接矩阵,且令两个顶点之间不存在的边的权值为机内允许的最大值(INT_MAX),则普里姆算法如算法7.9所示。
算法7.9
void MiniSpanTree_PRIM(MGraph G, VertexType u){
//用普里姆算法从第u个顶点出发构造网G的最小生成树T,输出T的各条边
//记录从顶点集U到V-U的代价最小的边的辅助数组定义:
// struct{
// VertexType adjvex;
// VRType lowcost;
// }closedge[MAX_VERTEX_NUM];
k = LocateVex(G, u);
for(j = 0;j<G.vexnum; j++)
if(j != k)
closedge[j] = {u, G.arcs[k][j]}; //{adjvex, lowcost}
closedge[k].lowcost = 0; //初始, U={u}
for(i = 1; i<G.vexnum; i++){ //选择其余G.vexnum-1个顶点
k = mininum(closedge); //求出T的下一个节点: 第k顶点
// MIN{closedge[vi].lowcost | closedge[vi].lowcost > 0, vi ∈ V-U}
printf(closedge[k].adjvex, G.vexs[k]);
closedge[k].lowcost = 0; //第k顶点并入U集
for(j = 0;j<G.vexnum; j++){
if(G.arcs[k][j].adj < closedge[j].lowcost) //新顶点并入U后重新选择最小边
closedge[j] = {G.vexs[k], G.arcs[k][j].adj};
}
}
}例如,对图7.16(a)中的网,利用算法7.9,将输出生成树上的5条边为:{(v1,v3}, (v3,v6), (v6,v4), (v3,v2), (v2,v5)}。
分析算法7.9,假设网中有n个顶点,则第一个进行初始化的循环语句的频度为n,第二个循环语句的频度为n-1。其中有两个内循环: 其一是在closedge[v].lowcost中求最小值,其频度为n-1;其二是重新选择具有最小代价的边,其频度为n。由此,普里姆算法的时间复杂度为O(n^2),与网中的边数无关,因此适用于求边稠密的网的最小生成树。
而克鲁斯卡尔算法恰恰相反,它的时间复杂度为O(eloge)(e为网中边的数目),因此它相对于普里姆算法而言,适合于求边稀疏的网的最小生成树。
克鲁斯卡尔算法从另一种途径求网的最小生成树。假设连通网N=(V, {E}),则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V, {}),图中每个顶点自成一个连通分量。在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。依次类推,直至T中所有顶点都在同一连通分量上为止。
例如,图7.18所示为依照克鲁斯卡尔算法构造一棵最小生成树的过程。代价分别为1,2,3,4的4条边满足上述条件,则先后被加入到T中,代价为5的两条边(v1,v4)和(v3,v4)被舍去。
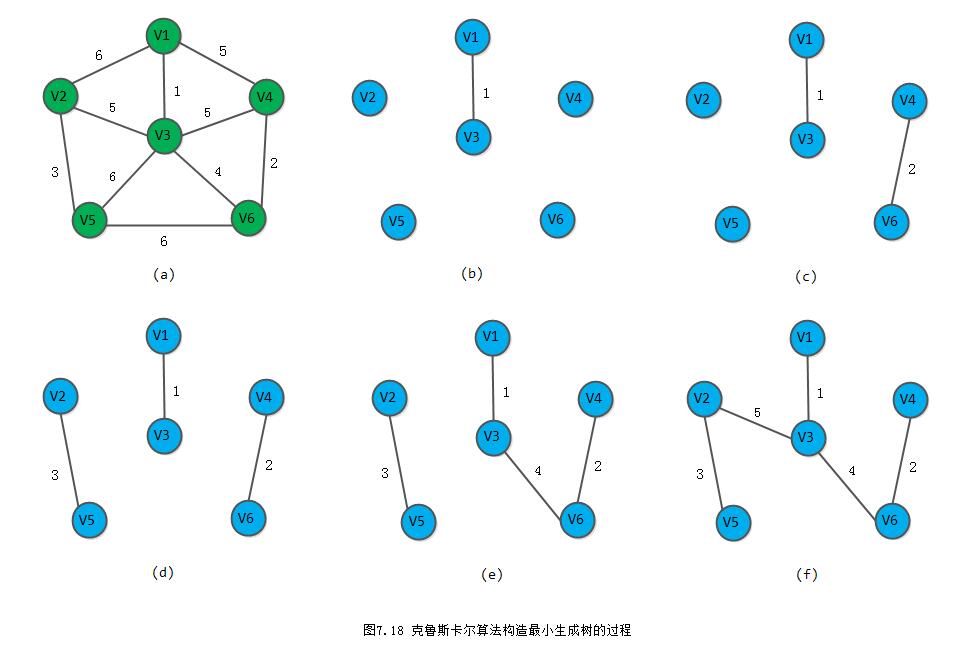
因为它们依附的两顶点在同一连通分量上,它们若加入T中,则会使T中产生回路,而下一条代价(=5)最小的边(v2,v3)连接两个连通分量,则可加入T。由此,构造成一棵最小生成树。下面我们根据上面的描述,写出一个克鲁斯卡尔算法的实现:
void MiniSpanTree_KRUSKAL(MGraph G){
//用克鲁斯卡尔构造网G的最小生成树T,输出T的各条边
//构造最小生成树的辅助结构
// struct{
// VertexType adjvex; //顶点
// int ccSeq; //该顶点所属连通分量
// int prev; //指向前一个与自己处于同一个连通分量的节点
// int next; //指向下一个与自己处于同一个连通分量的节点
// }ccnode[MAX_VERTEX_NUM];
int ccCount; //用于记录当前连通分量的个数
for(i = 0;i<G.vexnum; i++){
ccnode[i] = {G.vexs[i], i, i, i}; //初始时,每个顶点自成一个连通分量(ccSeq=i)
}
ccCount = G.vexnum; // 初始时每个顶点自成一个连通分量,因此总的连通分量个数为G.vexnum。
// ccCount值为1时,说明只剩下一个连通分量了,即完成了最小生成树的构建
while(ccCount > 1 && e-- ){ //e是边的条数
//从G中剩余的边中选出代价最小的边,返回该边对应的两个节点的节点号
i, j = mininum(G);
if(ccnode[i].ccSeq != ccnode[j].ccSeq){
//两个顶点分别属于不同的连通分量,可以合并,且合并后的连通分量ccSeq取较低的那个
low = i, high = j;
if(ccnode[j].ccSeq < ccnode[i].ccSeq){
low = j;
high = i;
}
setseq(high, ccnode[low].ccSeq); //将高段的ccSeq重置为lowSeq
splice(low, high); //拼接这两个分段
printf(ccnode[i].adjvex, ccnode[j].adjvex);
ccCount--;
}
}
}上述算法至多对e条边各扫描一次,假若以后面介绍的堆来存放网中的边,则每次选择最小代价的边仅需O(loge)的时间(第一次需O(e))。又生成树T的每个连通分量可看成是一个等价类,则构造T加入新的边的过程类似于求等价类的过程,由此可以采用前面介绍的MFSet类型来描述T,使构造T的过程仅需O(eloge)的时间,由此,克鲁斯卡尔算法的时间复杂度为O(eloge)。
3. 关节点和重连通分量
假若在删去顶点v以及和v相关联的各边之后,将图的一个连通分量分割成两个或两个以上的连通分量,则称顶点v为该图的一个关节点(articulation point)。一个没有关节点的连通图称为是重连通图(biconnected graph)。在重连通图上,任意一对顶点之间至少存在两条路径,则在删去某个顶点以及依附于该顶点的各边时也不破坏图的连通性。若在连通图上至少删去k个顶点才能破坏图的连通性,则称此图的连通度为k。关节点和重连通在实际中有较多应用。显然,一个表示通信网络的图的连通度越高,其系统越可靠,无论是哪一站点出现故障或遭到外界破坏,都不影响系统的正常工作;又如,一个航空网络若是重连通的,则当某条航线因天气等某种原因关闭时,旅客仍可从别的航线绕道而行;再如,若将大规模集成电路的关键线路设计成重连通的话,则在某些元件失效的情况下,整个片子的功能不受影响,反之,在战争中,若要摧毁敌方的运输线,仅需破坏其运输网中的关节点即可。
例如,下面图7.19中图G5是连通图,但不是重连通图。图中有4个关节点A、B、D和G。若删去顶点B以及所有依附顶点B的边,G5就被分割成3个连通分量{A、C、F、L、M、J}、{G、H、I、K}和{D、E}。类似地,若删去顶点A或D或G以及所有依附于它们的边,则G5被分割成两个连通分量,由此,关节点亦称割点。
利用深度优先搜索便可求得图的关节点,并由此可判别图是否是重连通的。
![]()
上图(图7.20)所示为从顶点A出发深度优先搜索遍历图G5所得深度优先生成树,图中实线表示树边,虚线表示回边(即不在生成树上的边)。对树中任一顶点v而言,其孩子节点为在它之后搜索到的邻接点,而其双亲节点和由回边联结的祖先节点是在它之前搜索到的邻接点。由深度优先生成树可得出两类关节点的特性:
1) 若生成树的根有两棵或两棵以上的子树,则此根顶点必为关节点。因为图中不存在联结不同子树中顶点的边,因此,若删去根节点,生成树便变成生成森林。如图7.20中的顶点A
2) 若生成树中某个非叶子顶点v,其某棵子树的根和子树中的其他节点均没有指向v的祖先的回边,则v为关节点。因为,若删去v,则其子树和图的其他部分被分割开来。如图7.20中的顶点B、D和G。
若对图Graph=(V, {E})重新定义遍历时的访问函数visited,并引入一个新的函数low,则由一次深度优先搜索遍历便可求得连通图中存在的所有关节点。
定义visited[v]为深度优先搜索遍历连通图时访问顶点v的次序号;定义:

注: low[v]的含义可理解为访问顶点v时可遇见的最低访问顺序
若对于某个顶点v,存在孩子节点w且low[w]>=visited[v],则该顶点v必为关节点。因为w是v的孩子节点时,low[w]>=visited[v],表明w及其子孙均无指向v的祖先的回边。
由定义可知,visited[v]即为v在深度优先生成树的前序序列中的序号,只需将DFS函数中头两个语句改为visited[v0]=++count(在DFSTraverse中设置初值count=1)即可;low[v]可由后序遍历深度优先生成树求得,而v在后序序列中的次序和遍历时遍历时退出DFS函数的次序相同,由此修改深度优先搜索遍历的算法便可得到求关节点的算法(见算法7.10和算法7.11)。
算法7.10
void FindArticul(ALGraph G)
{
//连通图G以邻接表作存储结构,查找并输出G上全部关节点。全局量count
//对访问计数
count = 1; visited[0] = 1; //设定邻接表上0号顶点为生成树的根
for(i = 1; i<G.vexnum;i++)
visited[i] = 0; //其余顶点尚未访问
p = G.vertices[0].firstarc; v=p->adjvex;
DFSArticul(G, v); //从第v顶点出发深度优先查找关节点
if(count < G.vexnum){
printf(0, G.vertices[0].data); //根是关节点,输出
while(p->nextarc){
p = p->nextarc;
v = p->adjvex;
if(visited[v] == 0)
DFSArticul(G, v);
}
}
}算法7.11
void DFSArticul(ALGraph G, int v0){
//从第v0个顶点出发深度优先遍历图G,查找并输出关节点
visited[v0] = min = ++count; //v0是第count个访问的顶点
for(p = G.vertices[v0].firstarc, p; p = p->nextarc){ //对v0的每个邻接顶点进行检查
w = p->adjvex; //w为v0的邻接顶点
if(visited[w] == 0){ //w未曾访问,是v0的孩子
DFSArticul(G, w); //返回前求得low[w]
if(low[w] < min)
min = low[w];
if(low[w] >= visited[v0])
printf(v0, G.vertices[v0].data); //关节点
}
else if(visited[w] < min){ //w已访问,w是v0在生成树上的祖先
min = visited[w];
}
}
low[v0] = min;
}例如,图G5中各顶点计算visited和low的函数值如下所列:
i | 0 1 2 3 4 5 6 7 8 9 10 11 12
---------------------------------------------------------------------------------------------------------
G.vertices[i].data | A B C D E F G H I J K L M
---------------------------------------------------------------------------------------------------------
visited[i] | 1 5 12 10 11 13 8 6 9 4 7 2 3
---------------------------------------------------------------------------------------------------------
low[i] | 1 1 1 5 10 1 5 5 8 2 5 1 1
---------------------------------------------------------------------------------------------------------
求的low值的顺序 | 13 9 8 7 6 12 3 5 2 1 4 11 10
其中J是第一个求得low值的顶点,由于存在回边(J,L),则low[J]=Min{visited[j], visited[L]}=2。顺便提一句,上述算法中将指向双亲的树边也看成是回边,由于不影响关节点的判别,因此,为使算法简明起见,在算法中没有区别之。
由于上述算法的过程就是一个遍历的过程,因此,求关节点的时间复杂度仍为O(n+e)。若尚需输出双连通分量,仅需在算法中增加一些语句即可,在此不再详述,留给读者自己完成。

